«ДОЛИ И ЧАСТИ»

Цели работы:
1. Ввести понятия умножения и деления числа на дробь, установив связь этих действий с вычислением части данного числа и восстановлением значения числа по его части и соответствующей ей дроби.
2. Изучить различные типы задач на части.
3. Разработать «опорный сигнал», способствующий решению простейших типовых задач на части.

ПРОБЛЕМА:
● В русском языке слово «умножить» означает «увеличить», а слово «разделить» означает «уменьшить». Так и происходит, когда мы умножаем или делим данное число m на натуральное число n.
● Однако произведение (т.е. результат умножения) числа m на правильную дробь p/q меньше, чем число m, а частное от деления числа m на правильную дробь p/q больше, чем число m.
● Мы хотим разобраться в этом противоречии, которое смущало еще средневековых математиков.

Исторически понятие произведения данного числа m на натуральное число n возникло как обобщение понятия суммы n слагаемых, каждое из которых равно m:
Произведение данного числа m на натуральное число n
Таким образом, для того, чтобы умножить m на n, нужно взять число m в качестве слагаемого n раз, т.е. результат увеличится в n раз.
n слагаемых
m⋅ n = m+…+m .

Произведение данного числа m на обыкновенную дробь p/q
Эту операцию мы связываем с вычислением «пэ-кутой» части от числа m.
Как это сделать на практике?
Для этого необходимо разделить число 24 на 8 равных частей и взять 5 из них.
Рассмотрим конкретный пример.
Пусть требуется найти 5/8 частей от числа 24.

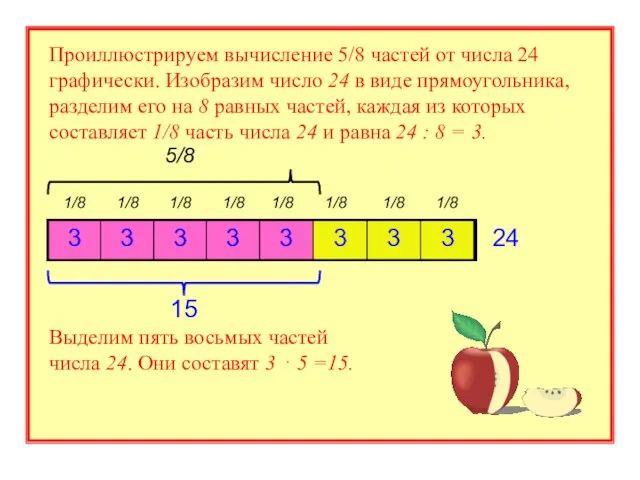
1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8
24
15
5/8
Проиллюстрируем вычисление 5/8 частей от числа 24 графически. Изобразим число 24 в виде прямоугольника, разделим его на 8 равных частей, каждая из которых составляет 1/8 часть числа 24 и равна 24 : 8 = 3.
Выделим пять восьмых частей числа 24. Они составят 3 ⋅ 5 =15.

Анализ: Чтобы решить эту задачу, необходимо, как было показано выше, найти 5/8 частей от числа 24.
Задача №1. Найти произведение данного числа 24 на обыкновенную дробь 5/8.
Решение.
Вывод: Мы убеждаемся, что при умножении числа 24 на дробь 5/8 получается число 15, которое меньше, чем 24.
Примечание. Оформляя решение, мы учитывали, что двоеточие и дробная черта являются равноправными знаками деления.

Анализ: Мы определили умножение данного числа на дробь как нахождение части числа, соответствующей данной дроби. Очевидно, что справедливо и обратное, т.е., например, чтобы найти 5/8 частей от числа 24, нужно умножить 24 на дробь 5/8.
Задача №2. Найти 5/8 частей от числа 24.
Решение.
Ответ: 5/8 частей числа 24 равны 15.

Определение произведения двух дробей
Мы уже выяснили, что для умножения числа m на дробь p/q необходимо разделить m на знаменатель q и умножить на числитель p:
Если число m также является дробью вида k/l, то его произведение на дробь p/q примет следующий вид:

Частное от деления данного числа m на обыкновенную дробь p/q
Рассмотрим конкретный пример. Пусть требуется найти число М, 3/7 части которого равны 12.
Эту операцию мы связываем с восстановлением значения числа М, для которого m является его «пэ-кутой» частью.
1) Для решения этой задачи необходимо разделить число 12 на 3 равные части. При этом мы узнаем, чему равна одна седьмая часть искомого числа: 12 : 3 = 4.
2) Все число М состоит из семи седьмых частей, поэтому М = 4 ⋅ 7 = 28.
Итак,

Выводы:
1. В результате деления числа 12 на правильную дробь 3/7 получилось число 28, которое больше, чем 12.
2. Правило деления числа m на дробь p/q:
3. Правило деления дроби m/n на дробь p/q:
4. Для того, чтобы восстановить число М, если известно, что «пэ-кутая» часть этого числа равна m, необходимо разделить m на дробь p/q:

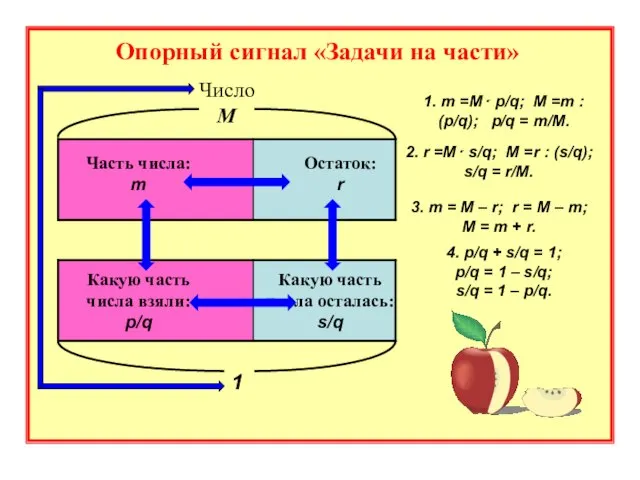
Опорный сигнал «Задачи на части»
Число М
Часть числа: m
Остаток: r
Какую часть числа взяли: p/q
Какую часть числа осталась: s/q
1
1. m =M⋅ p/q; M =m : (p/q); p/q = m/M.
2. r =M⋅ s/q; M =r : (s/q); s/q = r/M.
3. m = M – r; r = M – m; M = m + r.
4. p/q + s/q = 1; p/q = 1 – s/q; s/q = 1 – p/q.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ НА ЧАСТИ

Задача №3.
Масса медно-никелевого сплава M=7,7 кг. Найдите массу меди m и массу никеля r в отдельности, если масса меди составляет p/q = 5/11 частей от массы сплава. Какую часть (s/q) массы сплава составляет масса никеля?
Краткое условие
Дано: М = 7,7 кг;
p/q = 5/11.
Найти: m, r, s/q.
Решение.
2) r = M – m = 7,7 – 3,5 = 4,2 (кг);
3) s/q = r : M = 4,2 : 7,7 = 6/11.
Проверка: p/q + s/q = 5/11 + 6/11 =11/11 = 1.
Ответ: m = 3,5 кг; r = 4,2 кг; s/q = 6/11.
M
1

Решение.
M
1
Задача №4.
Найдите массу медно-никелевого сплава M и массу меди m, если масса меди составляет p/q = 5/11 частей от массы сплава, а масса никеля равна r = 4,2 кг. Какую часть (s/q) массы сплава составляет масса никеля?
Краткое условие
Дано: r = 4,2 кг;
p/q = 5/11.
Найти: M, m, s/q.
1) s/q = 1 – p/q = 1 – 5/11 = 6/11;
3) m = M – r = 7,7 – 4,2 = 3,5 (кг).
Проверка: m : M = 3,5 : 7,7 = 5/11 = p/q.
Ответ: M = 7,7 кг; m = 3,5 кг; s/q = 6/11.

Решение.
M
1
Задача №5.
Найдите массу медно-никелевого сплава M, если масса меди m=3,5 кг, масса никеля r = 4,2 кг. Какую часть (p/q) масса меди и какую часть (s/q) масса никеля составляют от массы сплава?
Краткое условие
Дано: m = 3,5 кг;
r = 4,2 кг.
Найти: M, p/q, s/q.
1) M = m + r = 3,5 + 4,2 = 7,7 (кг);
Ответ: M = 7,7 кг; p/q = 5/11; s/q = 6/11.
Проверка: p/q + s/q = 5/11 + 6/11 = 1.
2) p/q = m : M = 3,5 : 7,7 = 5/11;
3) s/q = r : M = 4,2 : 7,7 = 6/11.

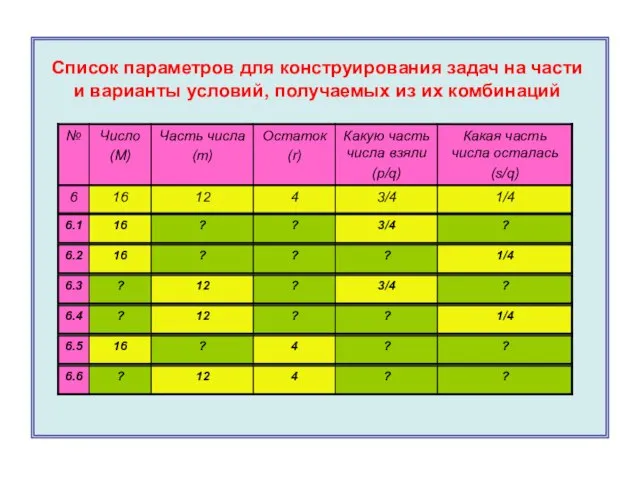
Список параметров для конструирования задач на части и варианты условий, получаемых из их комбинаций

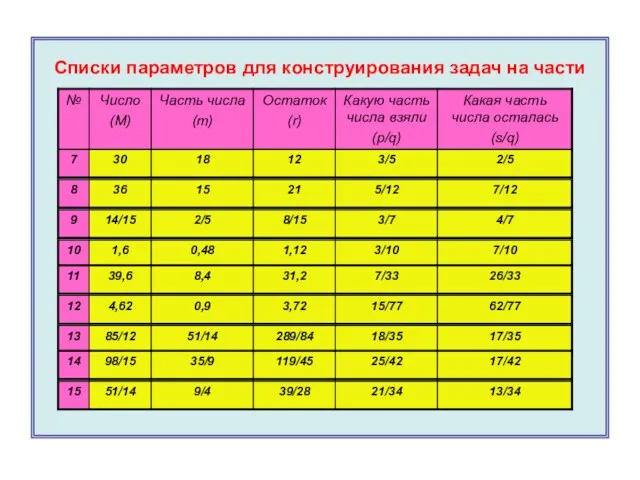
Списки параметров для конструирования задач на части

Пример решения задачи о трехдневном пути
Задача № 16.
Турист прошел в 1-й день 9/25 всего пути, во 2-й день — на 6 км больше, чем в 1-й день. Чему равен весь путь (S), и сколько километров было пройдено в 1-й и 2-й дни пути отдельно (S1 и S2), если в 3-й день турист прошел S3 =15 км?
Решение.
1) Примем за х путь S, пройденный туристом за 3 дня. Тогда S1 = 9/25 x, S2 = 9/25 x + 6.
2) Так как S = S1 + S2 + S3 , то можем составить уравнение:
x = 9/25 x + (9/25 x + 6) + 15, решая которое, получаем: х = 75.
3) Итак, S = 75 км, S1 = 9/25 ⋅ 75 = 27 (км), S2 = 27 + 6 = 33 (км).
Проверка: S1 + S2 + S3 = 27 + 33 + 15 = 75 (км) = S.
Ответ: S = 75 км, S1 = 27 км, S2 = 33 км.
S1 S2 S3
S

Задачи для самостоятельного решения
Ответы: 1) 85 км, 35 км, 30 км, 20 км. 2) 28 км, 32 км, 24 км.
3) 26 км, 32 км, 28 км.
Задача № 17.
Турист прошел в 1-й день 7/17 трехдневного пути, во 2-й день — 6/7 пути, пройденного в 1-й день. Чему равен весь путь (S), и сколько километров было пройдено в 1-й, 2-й и 3-й дни отдельно (S1 , S2 и S3), если в 3-й день турист прошел на 10 км меньше, чем во 2-й?
Задача № 18.
Турист прошел в 1-й день на 4 км меньше, чем во 2-й день, а в 3-й день — 2/5 пути, пройденного за два первых дня вместе. Сколько километров было пройдено в 1-й, 2-й и 3-й дни пути отдельно (S1 , S2 и S3), если всего за три турист прошел путь S = 84 км?
Задача № 19.
Турист прошел во 2-й день пути на 6 км больше, чем в 1-й день, а в 3-й день — 7/8 пути, пройденного во 2-й день. Сколько километров было пройдено в 1-й, 2-й и 3-й дни пути отдельно (S1 , S2 и S3), если всего за три турист прошел путь S = 86 км?