Движения

Движение
Преобразование одной фигуры в другую, при котором сохраняется расстояние между точками называется
движением.

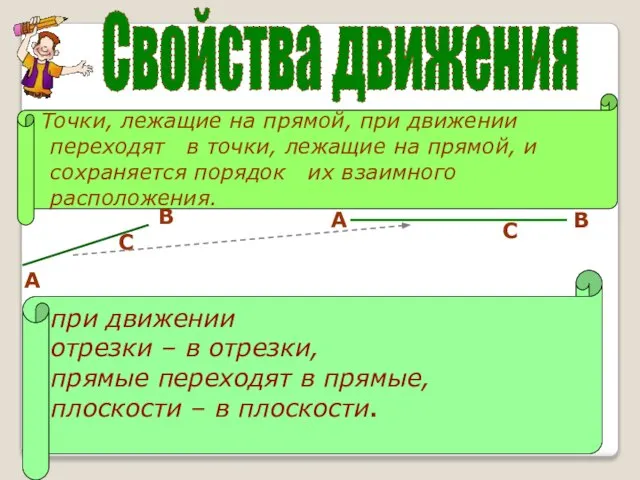
Свойства движения
Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
А
В
С
А
В
С
при движении
отрезки – в отрезки,
прямые переходят в прямые,
плоскости – в плоскости.

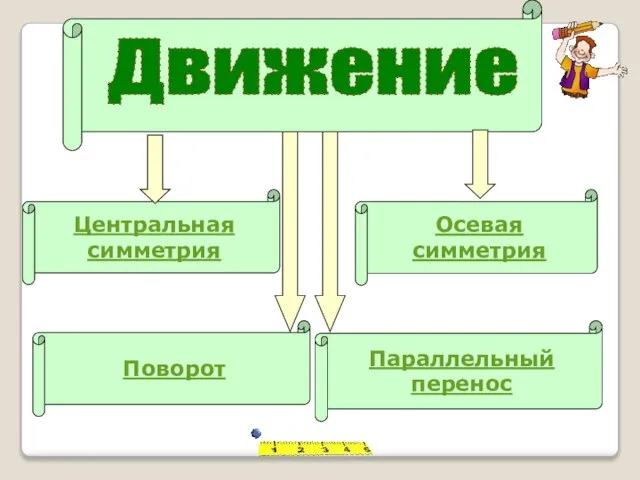
Движение
Центральная
симметрия
Поворот
Осевая симметрия
Параллельный
перенос

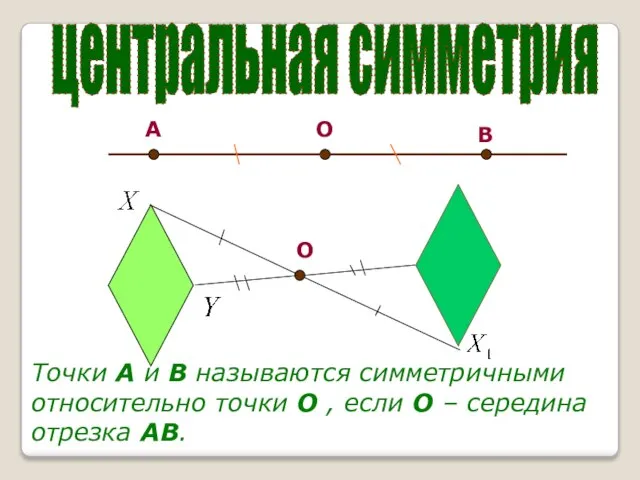
центральная симметрия
О
А
В
О
Точки А и В называются симметричными относительно точки О , если О – середина отрезка АВ.

ДОКАЖЕМ, ЧТО ЦЕНТРАЛЬНАЯ СИММЕТРИЯ, ЕСТЬ ДВИЖЕНИЕ (прочитайте стр.121-122)
А
Х
У
Z
В

Фигура называется центрально симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
О
О

Укажите координаты точек А1; В1; С1; К1 симметричных точкам А; В; С; К относительно начала координат, если:
А(3; -7; 1)
В(-4; 0; 8)
С(1,3; -5; -0,7)
К( -1; 5,6; 7,1)
А1 (-3; 7; -1)
В1 (4; 0; -8)
С1 (-1,3; 5; 0,7)
К1 (1; -5,6; -7,1)

Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а, если а серединный перпендикуляр к отрезку АА1
Осевая симметрия- отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.
А
А1
а

ДОКАЖЕМ, ЧТО ОСЕВАЯ СИММЕТРИЯ, ЕСТЬ ДВИЖЕНИЕ (прочитайте стр 122)
А
В
Х
У
Z
OZ

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией.