Содержание
- 2. Литература: 1. Кремер Н.Ш., Путко Б.А. Эконометрика. – М: «ЮНИТИ-ДАНА», 2008.-311 с. 2. Практикум по эконометрике
- 3. Введение (место дисциплины «эконометрика» в образовании, историческое обоснование её актуальности и общая характеристика содержания)
- 4. 1. Каковы традиции применения содержания дисциплины «эконометрика» в рамках российского экономического высшего образования? «Эконометрика» как дисциплина
- 5. 2.Чем исторически обосновывается актуальность эконометрики? Актуальность эконометрики иллюстрирует историческая справка о присуждении ряда Нобелевских премий за
- 6. 1969-Рагнар Фриш (Frisch, норвежский экономист, исследовал модели роста экономики, годы жизни: 1895-1973) и Ян Тинберген (Tinbergen,
- 7. 3. Какова общая характеристика современной эконометрики? Общая характеристика эконометрики такова – это наука, изучающая конкретные количественные
- 8. Тема 1. Предмет изучения дисциплины «эконометрика», ее место в экономике
- 9. 4. Какое место в экономическом образовании занимает дисциплина «эконометрика»? «Эконометрику» наряду с микро- и макроэкономикой в
- 10. 5. Как появился термин «эконометрика», как он трактовался изначально (широко, узко)? Термин «эконометрика» впервые был введен
- 11. 6. Как характеризовали эконометрику разные специалисты в период становления дисциплины? статистик С.Фишер представлял её как раздел
- 12. 7. Какие научные дисциплины определили появление эконометрики? Чем обусловлено её обособление в рамках экономики? в прошлом
- 13. Эконометрические модели зависимостей между показателями наряду с оценкой ожидаемых ошибок применимы при исследованиях макро- и микроэкономических
- 14. для прогнозирования (численного), в виде модельных блоков (для имитации) в рамках сложных модельных комплексов, а также
- 15. 8. Каким образом и параллельно с какими видами моделирования в экономике применяется эконометрическое моделирование в современных
- 16. 9. Как принято определять понятие «эконометрика» в наше время? «Эконометрика-это самостоятельная научная дисциплина, объединяющая совокупность теоретических
- 17. 10. Что выступает предметом изучения эконометрики? Предметом изучения эконометрики выступают социально-экономические системы (объекты, явления) в их
- 18. 11. Какие методы, в первую очередь, определяют содержание эконометрики? В первую очередь, содержание эконометрики определяют методы
- 19. 12. В чем основная цель практических приложений эконометрики и чем стимулируется её развитие? Основная цель практических
- 20. Тема 2. Общая характеристика эконометрического моделирования
- 21. 2.1. В чём основная цель применения эконометрической модели о связи между показателями? Имеются разные экономические показатели,
- 22. 2.2. Какова роль теории вероятностей, математической статистики в эконометрике? Эконометрическое моделирование предусматривает оперирование понятием «вероятность», предполагая
- 23. 2.3. Каков специальный математический смысл термина «регрессия», что является регрессией в статистическом смысле? Специальный математический смысл
- 24. 2.4. Как принято интерпретировать понятие «парная регрессия»? Понятие «парная регрессия», рассматриваемое в рамках специальных дисциплин, таких
- 25. 2.5. Как принято интерпретировать понятие «парная регрессия»? Точность, с которой уравнение регрессии величины Y по величине
- 26. 2.6. Как связаны детерминированная и случайная величины в рамках модели парной линейной регрессии? Типовые ситуации приложений
- 27. 2.7. В чём специфика эконометрической модели временных рядов? В моделях временных рядов (для «time-series data» –
- 28. 2.8. Что собой представляет эконометрическая модель «система одновременных уравнений»? Обобщением понятия регрессионная модель выступает модель в
- 29. 2.9. Каковы основные этапы эконометрического моделирования? Основные этапы вероятностно-статистического моделирования: постановочный, включает определение набора факторов, подразделение
- 30. Тема 3. Метод наименьших квадратов (МНК) для парной линейной регрессии
- 31. Рассмотрим задачу регрессионного анализа: будем восстанавливать линейную регрессионную зависимость величины Y от величины X в форме
- 32. Воспользуемся данными {Y i,X i, i=1,…,n} по проявлениям выявляемой зависимости в аналогичных условиях (при n ≥
- 33. Значения параметров функции a, b, найдем, минимизируя «видимые» ошибки-отклонения «прогнозов по функции» от «факта» – по
- 34. Согласно необходимому условию экстремума приравняем частные производные нулю, получим два уравнения: ∑ [2⋅(a+b·X i – Y
- 35. Откуда следует в общем случае, что b = (n⋅∑ X i⋅Y i – (∑ X i)
- 36. Если рассмотреть отклонения от средних хi= Xi-X 0, уi= Y i-Y0, то нетрудно убедиться, что средние
- 37. b = ∑ (X j – X 0) ⋅ (Y j – Y 0)/ ∑ (X
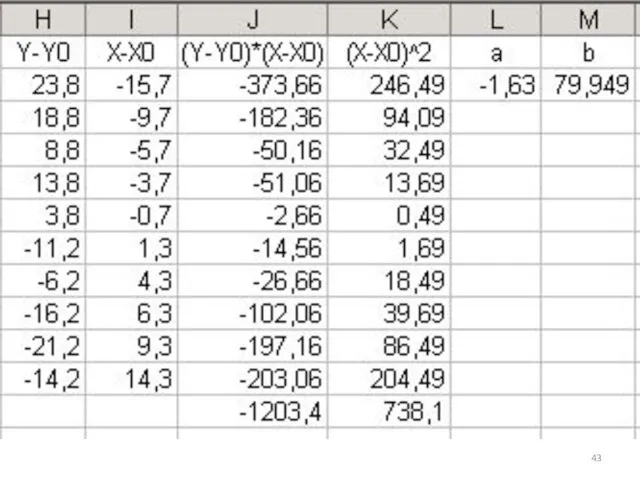
- 38. Упражнение (контрольное задание) № 1 (см.[3, с.41, Упр. 2.9]). Пусть имеется таблица данных двух показателей (Y,X),
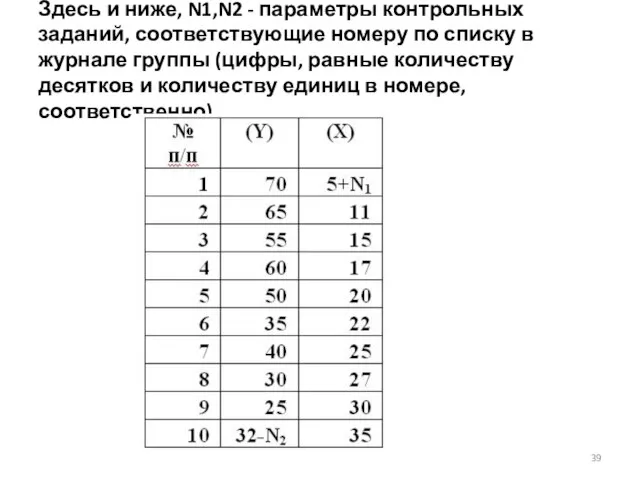
- 39. Здесь и ниже, N1,N2 - параметры контрольных заданий, соответствующие номеру по списку в журнале группы (цифры,
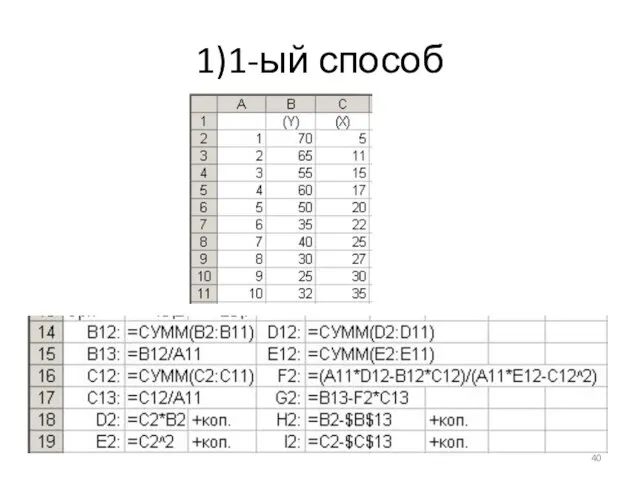
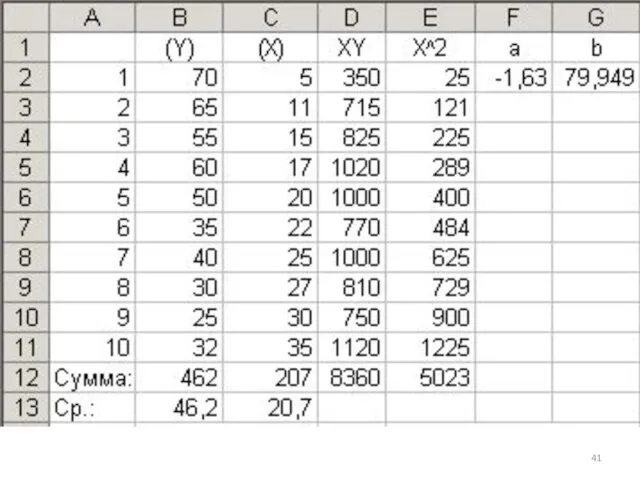
- 40. 1)1-ый способ
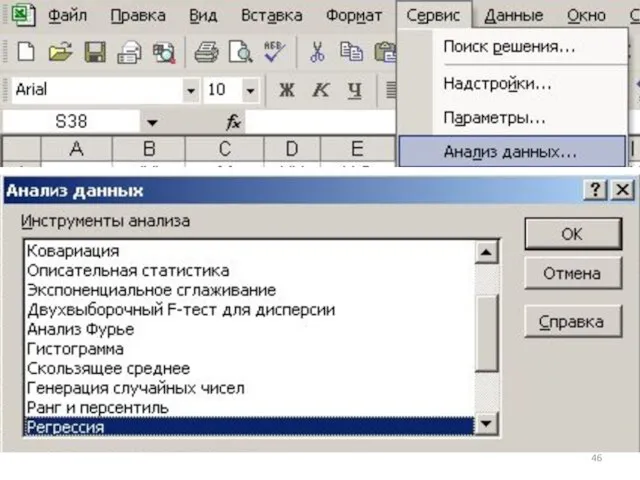
- 42. 2)2-ой способ
- 43. 2)2-ый способ
- 44. Если раздел меню «Сервис/Анализ данных…» не нашёлся, то открываем (инициируем выполнение команды меню) «Сервис/Надстройки…»… 3)3-ий способ
- 45. …и подключаем «Пакет анализа» (устанавливаем соответствующую «галочку»)…
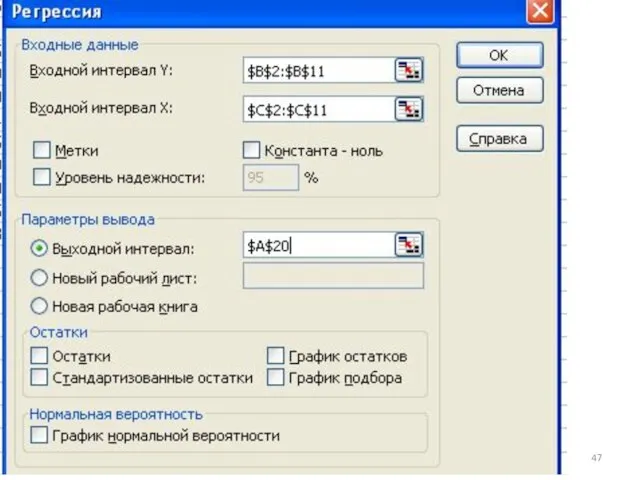
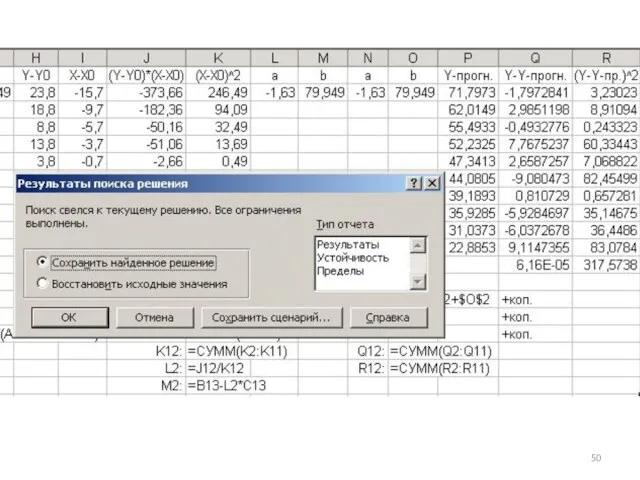
- 48. 4)4-ый способ
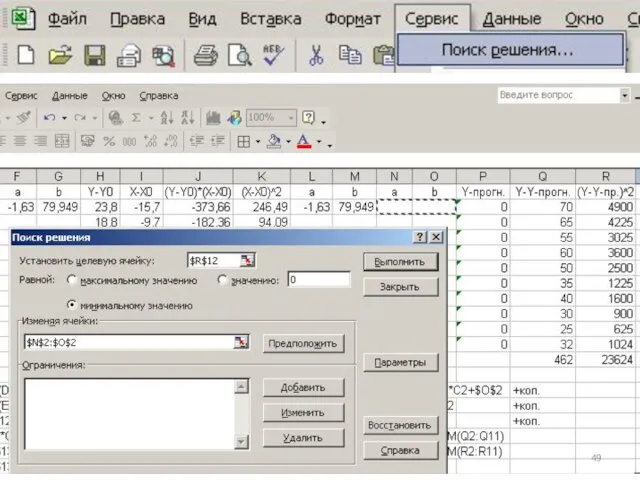
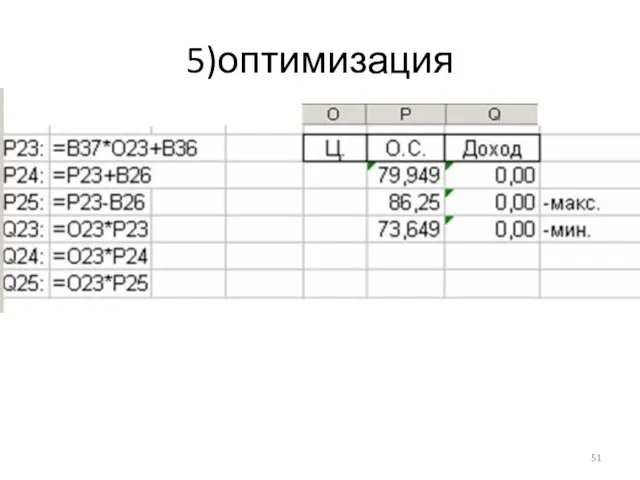
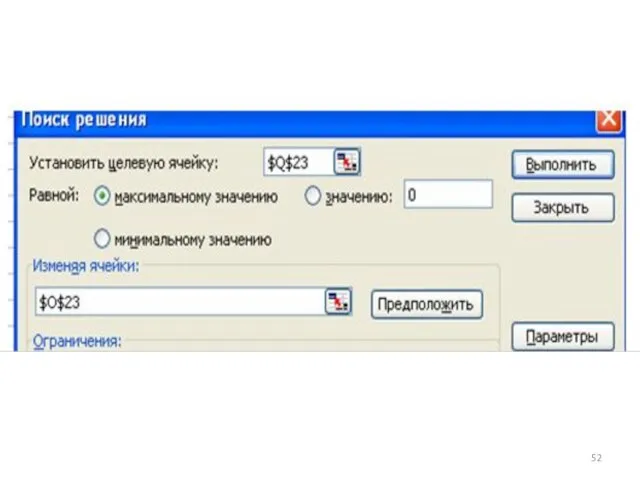
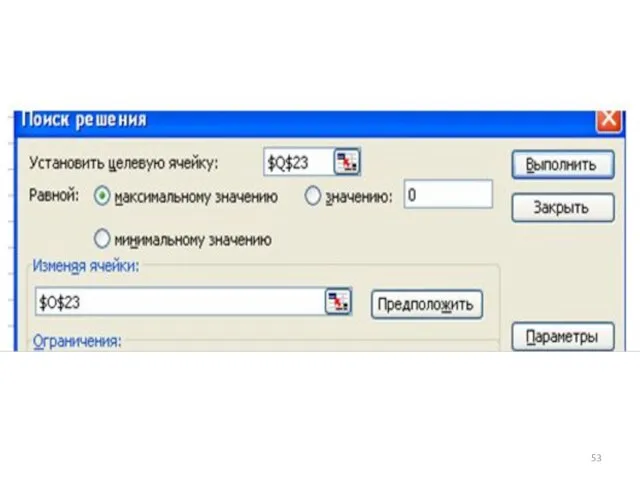
- 51. 5)оптимизация
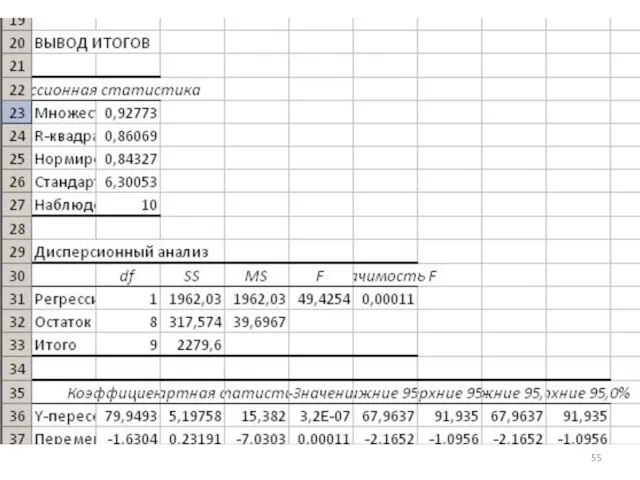
- 54. 6) Заметим, что соответствующую эконометрическю модель принято записывать, в частности, следующим образом (применяя одинаковый способ округления):
- 56. Для выполнения индивидуального варианта задания требуется: скопировать лист Excel, рассмотренный выше; внести изменения согласно инд.варианту в
- 57. Тема 4. МНК для множественной линейной регрессии
- 58. Рассмотрим задачу множественного регрессионного анализа: будем восстанавливать линейную регрессионную зависимость величины Y от величин X1, X2,
- 59. Воспользуемся данными {Yi, Xi1, Xi2, … , Xin, i=1,…,m} по проявлениям выявляемой зависимости в аналогичных условиях
- 60. Значения параметров функции b0 , b1, b2 ,…, bn найдем, минимизируя «видимые» ошибки-отклонения «прогнозов по функции»
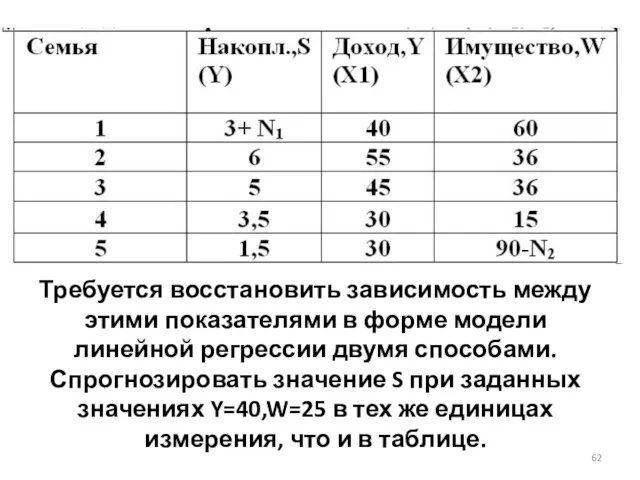
- 61. Упражнение (контрольное задание) № 2 (см.[3, с.63, Упр. 3.5]). Пусть имеется таблица данных трёх показателей S,Y,W(Y,X1,X2)
- 62. Требуется восстановить зависимость между этими показателями в форме модели линейной регрессии двумя способами. Спрогнозировать значение S
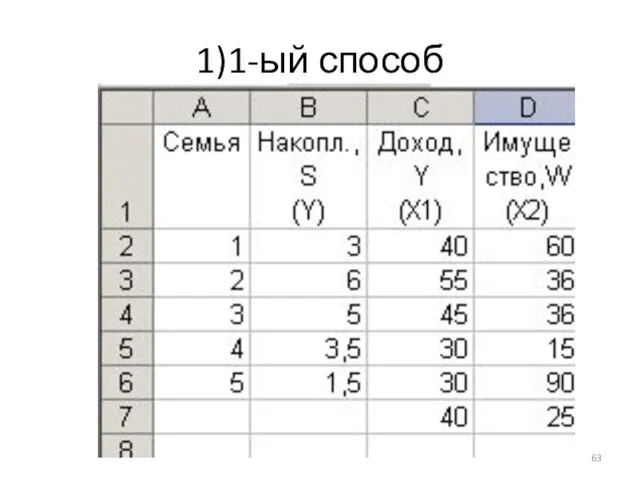
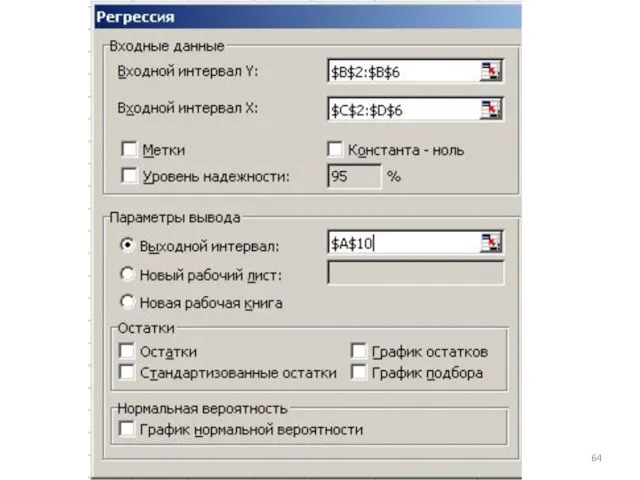
- 63. 1)1-ый способ
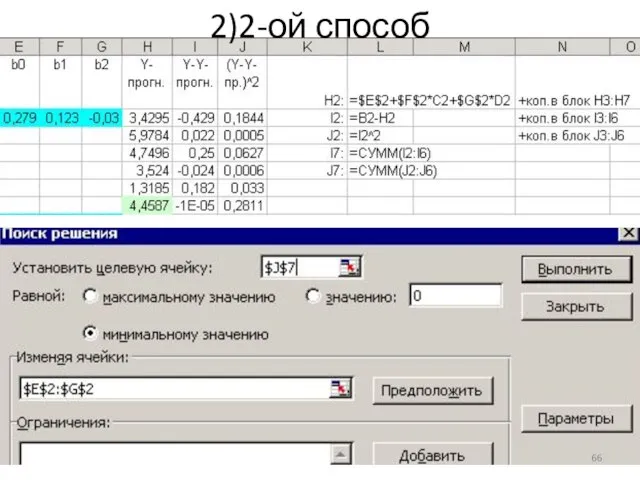
- 66. 2)2-ой способ
- 67. Второй способ прогнозирования B7:=b26+b27*c7+b28*d7 Оценка погрешности-в b16
- 69. Скачать презентацию



































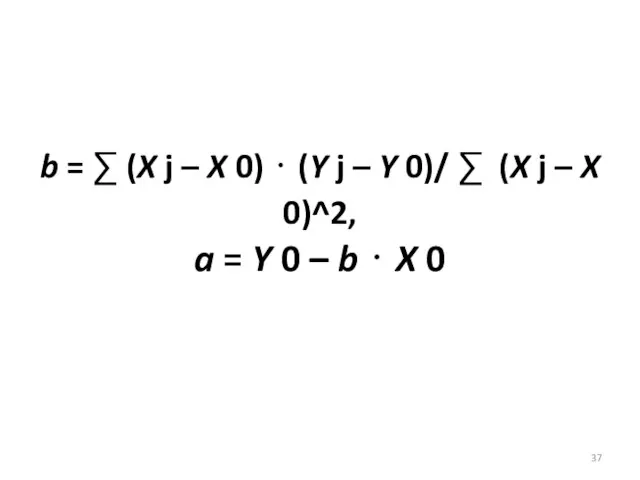
![Упражнение (контрольное задание) № 1 (см.[3, с.41, Упр. 2.9]). Пусть имеется таблица](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365537/slide-37.jpg)










![Упражнение (контрольное задание) № 2 (см.[3, с.63, Упр. 3.5]). Пусть имеется таблица](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365537/slide-60.jpg)


 Моделирование основных бизнес-процессов Jurby WaterTech International
Моделирование основных бизнес-процессов Jurby WaterTech International ЦЕЛЕВАЯ АУДИТОРИЯ Большинство Меньшинство
ЦЕЛЕВАЯ АУДИТОРИЯ Большинство Меньшинство ИНФОРМАЦИОННЫЕ МОДЕЛИ
ИНФОРМАЦИОННЫЕ МОДЕЛИ Решение задач с параметром графическим методом - один из аспектов подготовки к ЕГЭ
Решение задач с параметром графическим методом - один из аспектов подготовки к ЕГЭ Азбука родного края
Азбука родного края СИСТЕМЫ ВИДЕОНАБЛЮДЕНИЯВ ОФИСЕ
СИСТЕМЫ ВИДЕОНАБЛЮДЕНИЯВ ОФИСЕ Террасная доска из ДПК от производителя
Террасная доска из ДПК от производителя Общешкольное собраниена тему:«SOS!!! Вредные привычки»
Общешкольное собраниена тему:«SOS!!! Вредные привычки» «Q.events» является подразделением Рекламного Агентства «IQ», которое существует на рынке рекламы Санкт-Петербурга 10 лет. Основной ц
«Q.events» является подразделением Рекламного Агентства «IQ», которое существует на рынке рекламы Санкт-Петербурга 10 лет. Основной ц Вёр=ё темипе =ыхённё уроксенче усё курмалли материал
Вёр=ё темипе =ыхённё уроксенче усё курмалли материал Где ваша аудитория?
Где ваша аудитория? Дела давно минувшх дней, Преданья старины глубокой...
Дела давно минувшх дней, Преданья старины глубокой... Уравнение и его корни
Уравнение и его корни Система представления климатических данных через Интернет-портал ГГИ
Система представления климатических данных через Интернет-портал ГГИ Дифракция света
Дифракция света окрашивание тканей и органов
окрашивание тканей и органов Сертификат специалиста как условие допуска к осуществлению медицинской деятельности
Сертификат специалиста как условие допуска к осуществлению медицинской деятельности Методическое объединение учителей начальных классов
Методическое объединение учителей начальных классов Карта Олимпийского парка
Карта Олимпийского парка Пожарная профилактика
Пожарная профилактика  Разработка программного обеспечения для расчета показателей работы шлакового режима доменной печи Выполнил: Костромин А.В. Групп
Разработка программного обеспечения для расчета показателей работы шлакового режима доменной печи Выполнил: Костромин А.В. Групп Материалы и работа с ними
Материалы и работа с ними Организация системы дистанционного обучения: основы, методы, проблемы.
Организация системы дистанционного обучения: основы, методы, проблемы. ООО Завод Модульных Конструкций - один из крупнейших в РФ
ООО Завод Модульных Конструкций - один из крупнейших в РФ Гетероэпитаксия SiC-AlN/SiC/Si
Гетероэпитаксия SiC-AlN/SiC/Si Для пятиклассников
Для пятиклассников Открытые данные. Классификация информации в электронном правосудии
Открытые данные. Классификация информации в электронном правосудии Факторы развития дистрибьюторского сектора
Факторы развития дистрибьюторского сектора