Содержание
- 2. Теория функционала плотности основывается на теореме, сформулированной Хохенбергом и Коном, которая гласит, что полная энергия системы
- 3. Распределение электронной плотности n(r), которое минимизирует функционал энергии Е[n(r)], находится как самосогласованное решение системы одноэлектронных уравнений
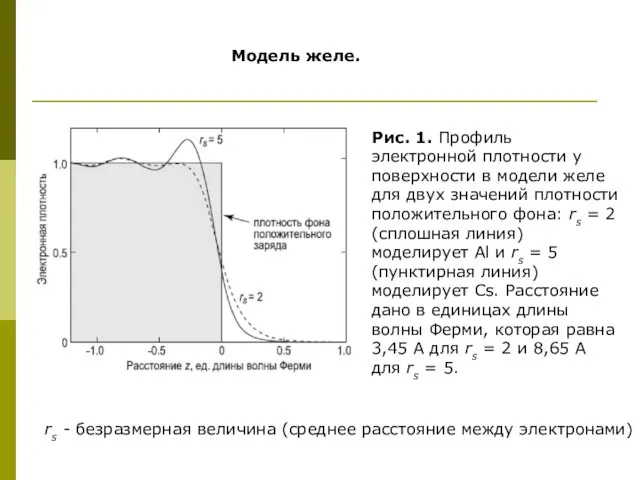
- 4. Рис. 1. Профиль электронной плотности у поверхности в модели желе для двух значений плотности положительного фона:
- 5. Давайте применим модель желе для задачи поверхности. Для полубесконечной поверхности с направлением z вдоль нормали к
- 6. Модель желе. Рис. 2. СТМ изображение (500x500 А2) в режиме постоянного тока от поверхности Cu(111), полученное
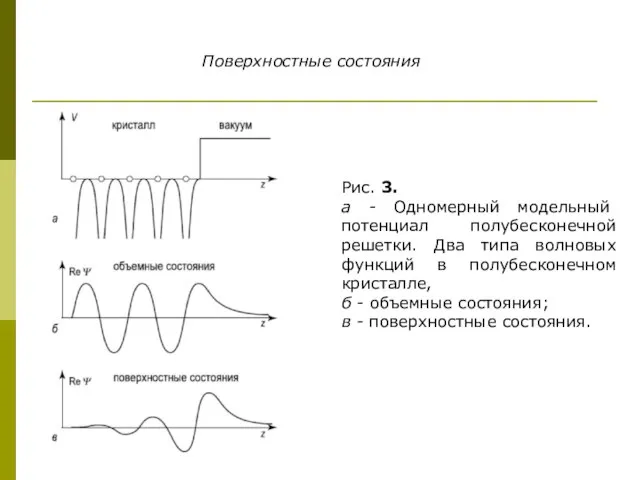
- 7. Поверхностные состояния Рис. 3. а - Одномерный модельный потенциал полубесконечной решетки. Два типа волновых функций в
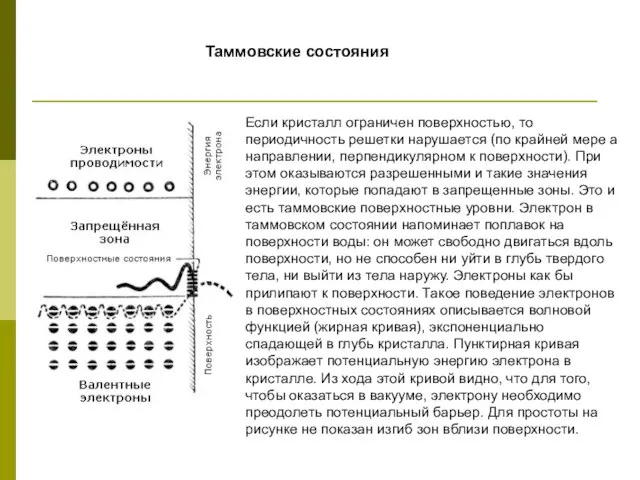
- 8. Таммовские состояния Если кристалл ограничен поверхностью, то периодичность решетки нарушается (по крайней мере а направлении, перпендикулярном
- 9. Поверхностные состояния Шокли можно объяснить неспаренными связями атомов, находящихся на поверхности. Например, при расколе кристалла создававшие
- 10. Поверхностная проводимость Рис. 4. Схематическая иллюстрация изгиба зон у поверхности полупроводника, а, б - n-типа; е,
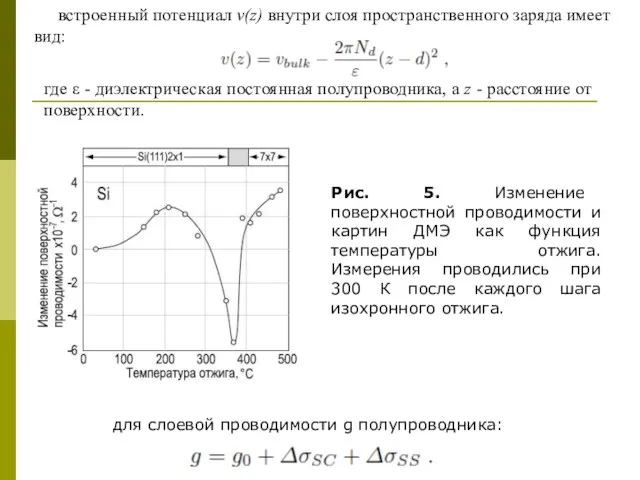
- 11. Рис. 5. Изменение поверхностной проводимости и картин ДМЭ как функция температуры отжига. Измерения проводились при 300
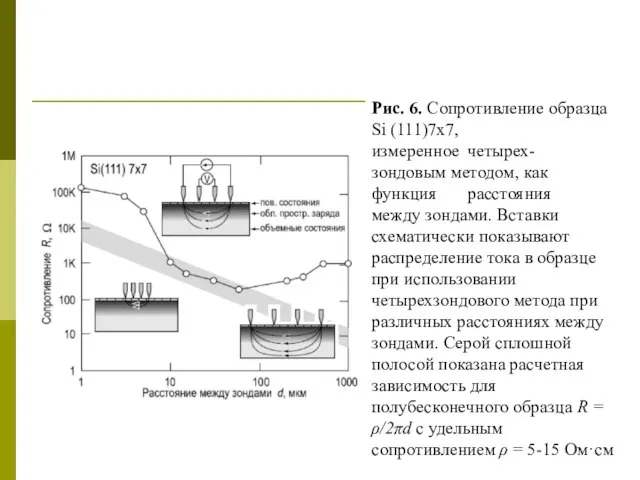
- 12. Рис. 6. Сопротивление образца Si (111)7x7, измеренное четырех- зондовым методом, как функция расстояния между зондами. Вставки
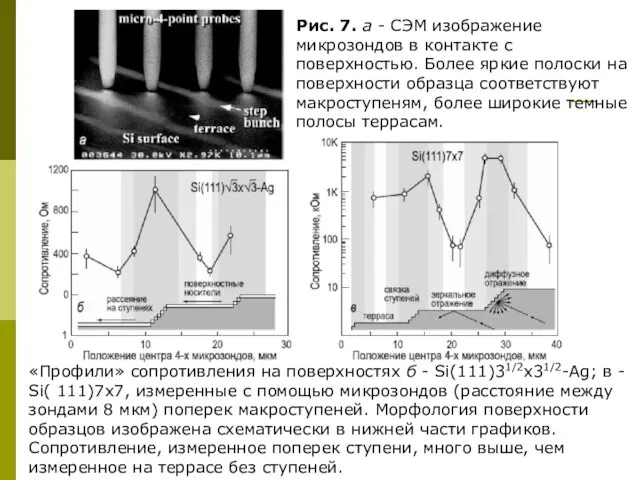
- 13. «Профили» сопротивления на поверхностях б - Si(111)31/2x31/2-Ag; в - Si( 111)7x7, измеренные с помощью микрозондов (расстояние
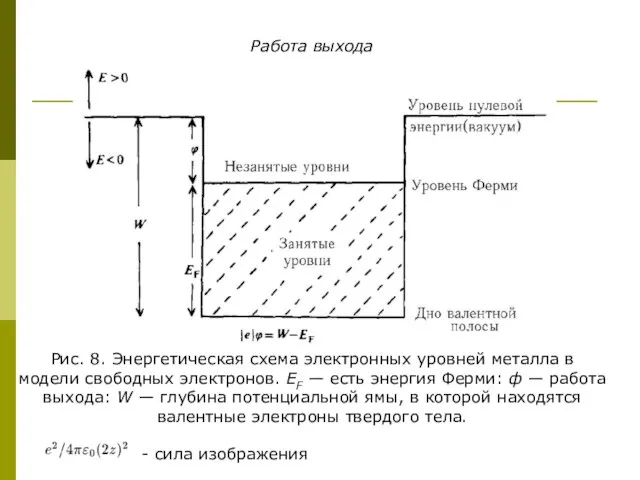
- 14. Работа выхода Рис. 8. Энергетическая схема электронных уровней металла в модели свободных электронов. ЕF — есть
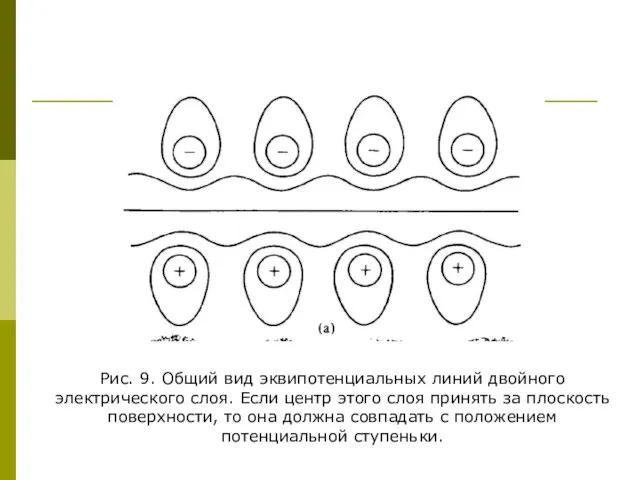
- 15. Рис. 9. Общий вид эквипотенциальных линий двойного электрического слоя. Если центр этого слоя принять за плоскость
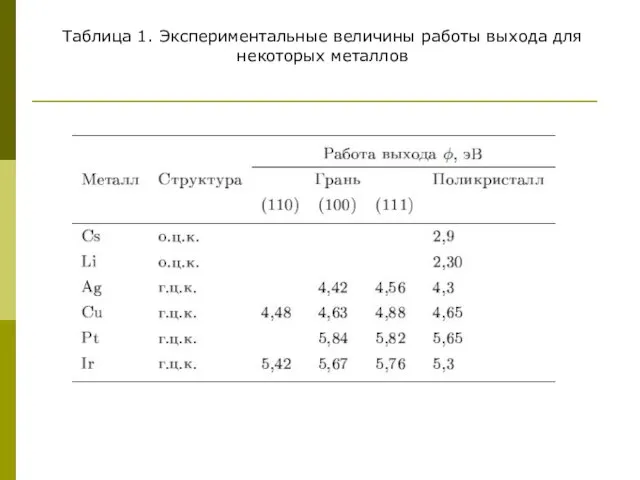
- 16. Таблица 1. Экспериментальные величины работы выхода для некоторых металлов
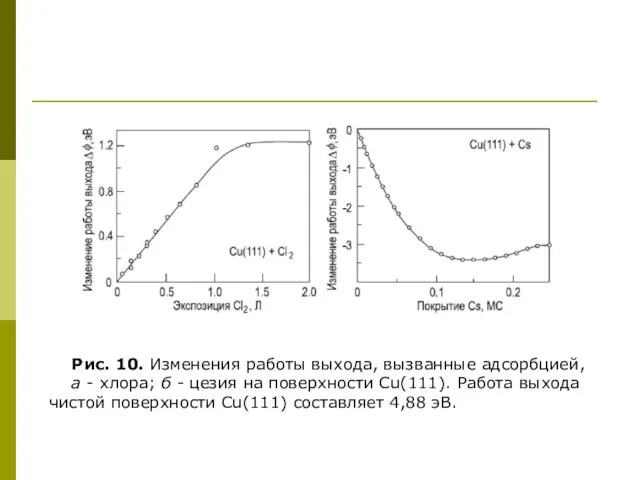
- 17. Рис. 10. Изменения работы выхода, вызванные адсорбцией, а - хлора; б - цезия на поверхности Cu(111).
- 18. Рис. 11. Схематическая зонная диаграмма для поверхности полупроводника, ф - работа выхода, χ - сродство к
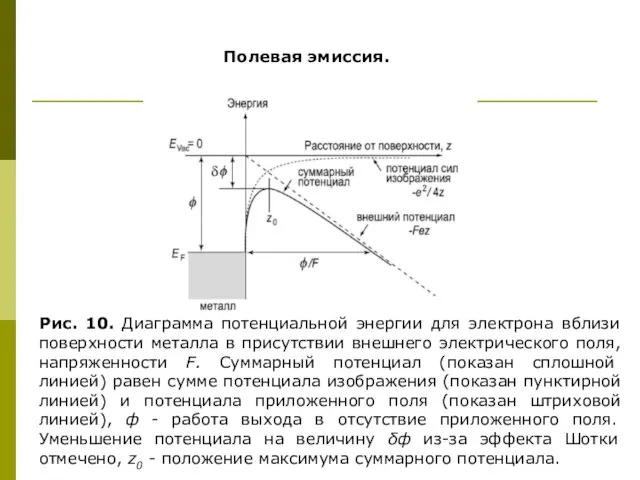
- 19. Полевая эмиссия. Рис. 10. Диаграмма потенциальной энергии для электрона вблизи поверхности металла в присутствии внешнего электрического
- 20. Плотность тока j для этого процесса описывается выражением Фоулера-Нордгейма: где F - это приложенное напряжение в
- 21. Термоэлектронная эмиссия. Плотность термоэлектронного тока j с однородной поверхности металла при температуре Т описывается выражением Ричардсона-Дэшмана:
- 23. Скачать презентацию

![Распределение электронной плотности n(r), которое минимизирует функционал энергии Е[n(r)], находится как самосогласованное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/376761/slide-2.jpg)







 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке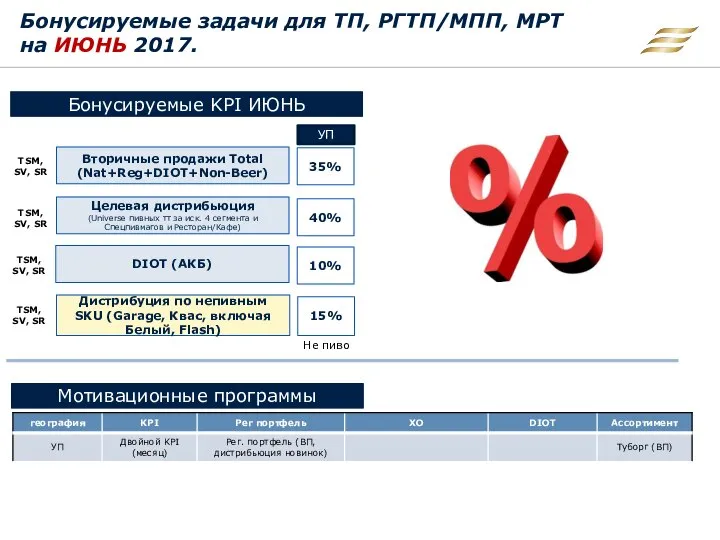 Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика