Содержание
- 2. Метод наибольшего правдоподобия Кроме метода моментов существуют и другие методы точечной оценки неизвестных параметров распределения. Например
- 3. Метод наибольшего правдоподобия
- 4. Метод наибольшего правдоподобия
- 5. Пример
- 6. Пример
- 7. Метод наибольшего правдоподобия
- 8. Пример
- 9. Пример
- 10. Условные варианты Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда Равноотстоящими
- 11. пример
- 12. Обычные, начальные и центральные эмпирические моменты Для вычислений сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения
- 13. Обычные, начальные и центральные эмпирические моменты
- 14. Условные эмпирические моменты. Отыскание центральных моментов по условным Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы
- 15. Условные эмпирические моменты. Отыскание центральных моментов по условным Выразим обычные моменты через условные: Для того чтобы
- 16. Задание на практическое занятие
- 17. Задание на практическое занятие
- 18. Задание на практическое занятие
- 20. Скачать презентацию

















 Цель кодирования
Цель кодирования История бирдекелей.
История бирдекелей. Познавательные способности
Познавательные способности Формирование УУД Педагогические технологии
Формирование УУД Педагогические технологии Tricks and jokes in Mass media
Tricks and jokes in Mass media Оценка неопределенности результатов экстракционного атомно-абсорбционного анализа
Оценка неопределенности результатов экстракционного атомно-абсорбционного анализа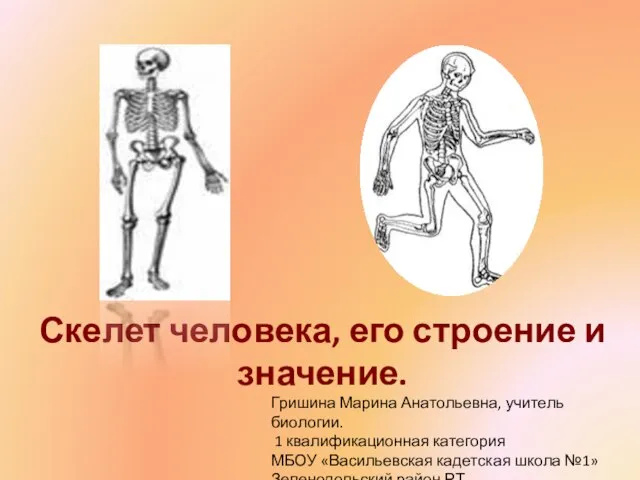 Презентация на тему Строение скелета человека (8 класс)
Презентация на тему Строение скелета человека (8 класс) Звуки речи. Фонетика
Звуки речи. Фонетика Шлифовальные станки
Шлифовальные станки Диоды и кенотроны. Устройство, физика работы. Схемные решения. Применения и параметры
Диоды и кенотроны. Устройство, физика работы. Схемные решения. Применения и параметры Определение, юридические признаки, стороны договора подряда
Определение, юридические признаки, стороны договора подряда Столкновение
Столкновение Урок – презентация
Урок – презентация Истоки холодной войны. Военно-политические блоки
Истоки холодной войны. Военно-политические блоки Финансовая стратегия бизнес-планирования
Финансовая стратегия бизнес-планирования «Я вас любил…» (Тверичанки, воспетые А.Пушкиным.)
«Я вас любил…» (Тверичанки, воспетые А.Пушкиным.) Предприятие как хозяйствующий субъект
Предприятие как хозяйствующий субъект Электронные больничные и прямые выплаты
Электронные больничные и прямые выплаты «Мы в Ильинской церкви»
«Мы в Ильинской церкви» Наука и искусство. Знание научное и знание художественное
Наука и искусство. Знание научное и знание художественное Презентация на тему Малая родина Бунина
Презентация на тему Малая родина Бунина Письмо Бога для тебя
Письмо Бога для тебя ТЕСТ "Геометрическая оптика"
ТЕСТ "Геометрическая оптика" W w w. a l a d d i n. r u Руководитель направления контент- безопасности Владимир Бычек
W w w. a l a d d i n. r u Руководитель направления контент- безопасности Владимир Бычек  Обосбление согласованных и несогласованных определений
Обосбление согласованных и несогласованных определений Комиссия по спортивно-массовой работе с работниками и их семьями
Комиссия по спортивно-массовой работе с работниками и их семьями Презентация на тему Древний Восток
Презентация на тему Древний Восток  ЛЕВ АЛЕКСЕЕВИЧ ШКОЛЬНЫЙ
ЛЕВ АЛЕКСЕЕВИЧ ШКОЛЬНЫЙ