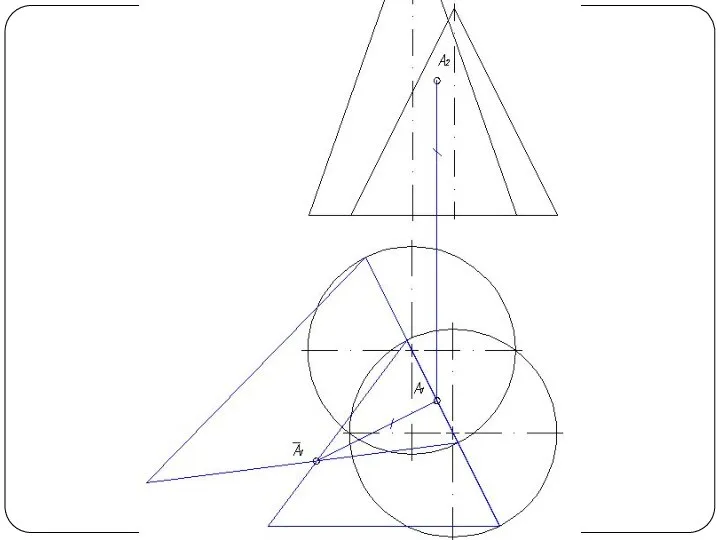
Слайд 2Наиболее общий способ построения линии пересечения двух поверхностей называется способом вспомогательных секущих

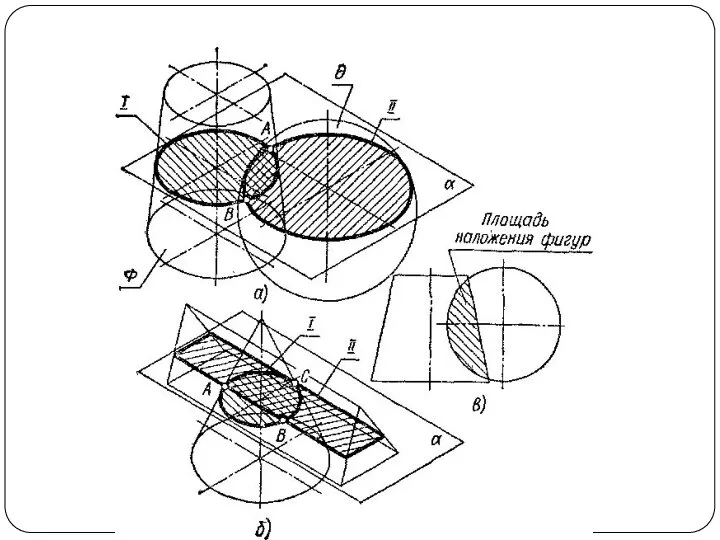
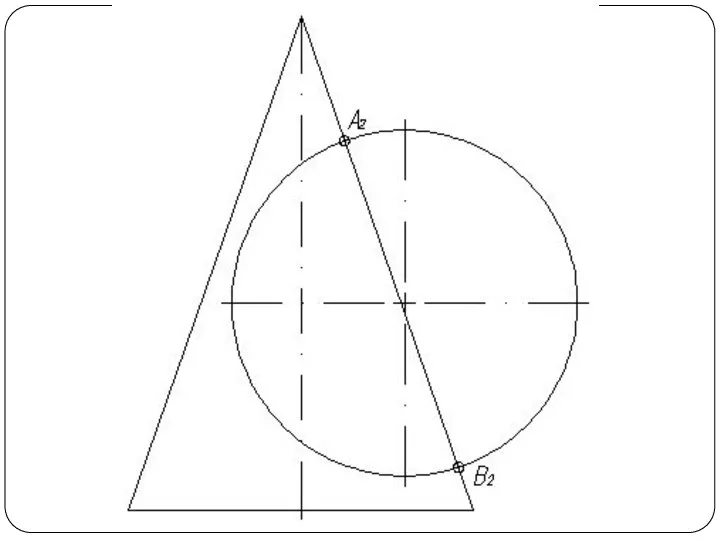
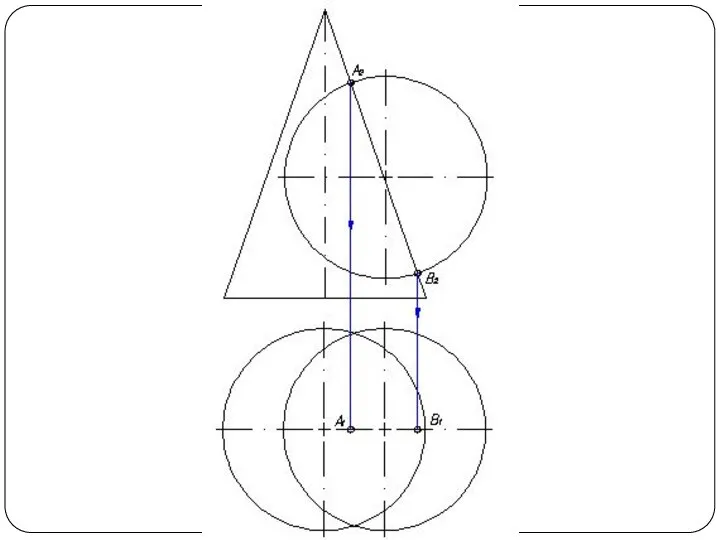
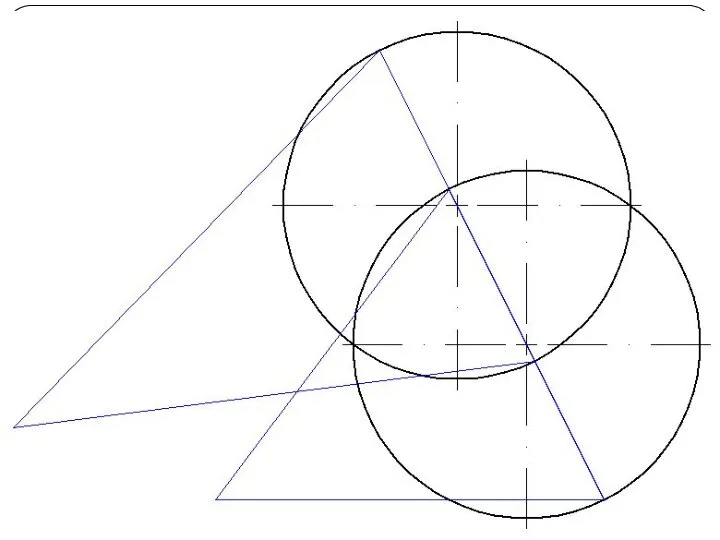
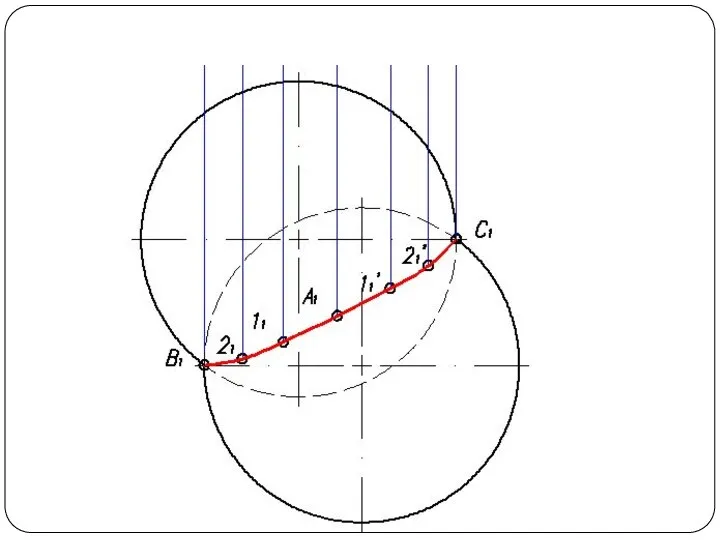
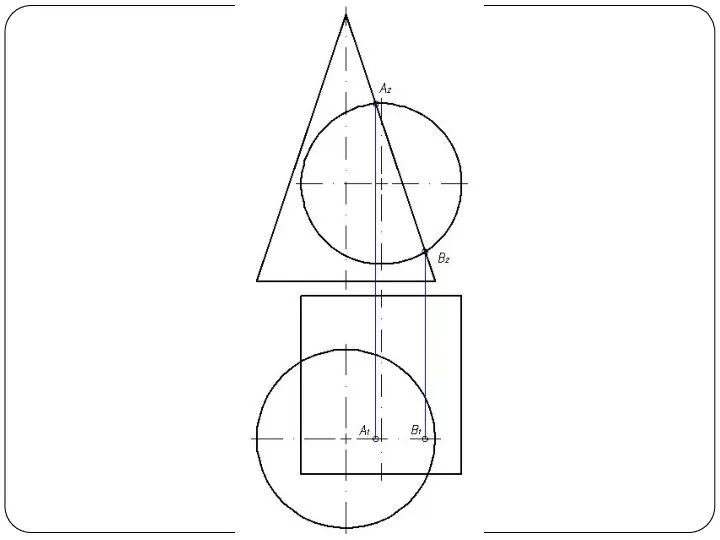
поверхностей или способом посредников. Сущность способа заключается в том, что две данные поверхности Φ и Θ (рис. 1а) пересекаются вспомогательными поверхностями или, в частном случае, вспомогательными плоскостями – посредниками. Каждый из посредников пересекает данные поверхности по линиям I и II, лежащим на одной и той же поверхности или в одной и той же плоскости. При взаимном пересечении этих линий получаются общие точки A и В, принадлежащие линии пересечения поверхностей.
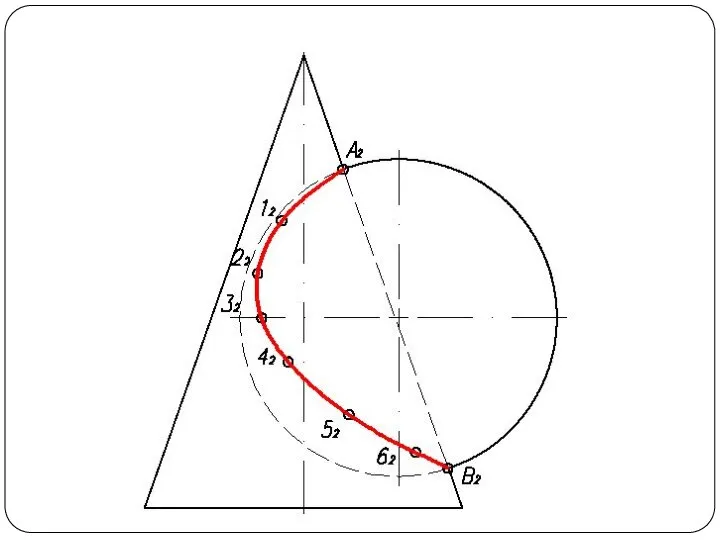
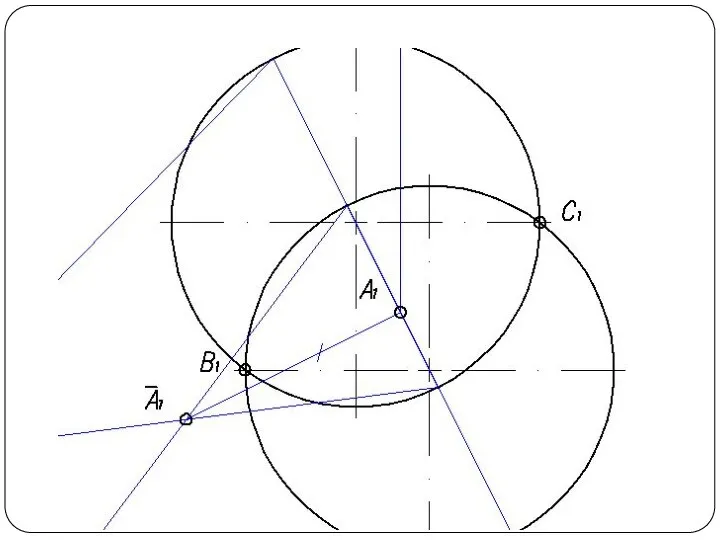
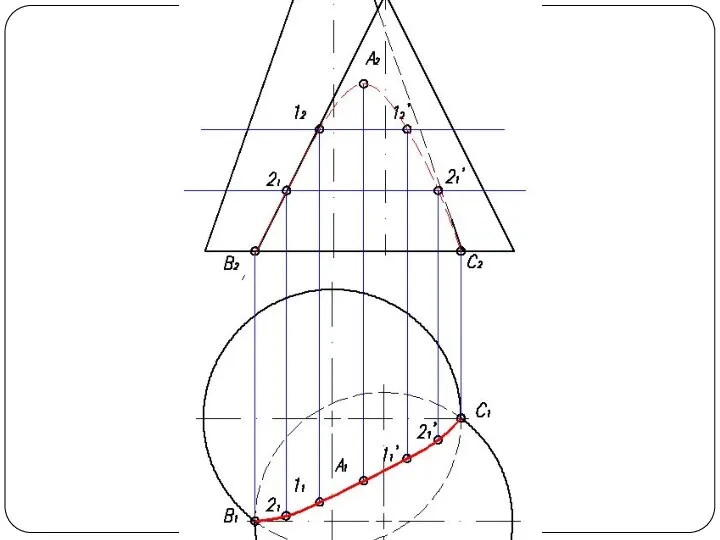
Слайд 4Повторяя указанный прием с различными вспомогательными поверхностями, находят такое количество точек, которое

вполне определяет линию пересечения. Полученные точки соединяют плавной кривой по лекалу.
Чаще применяют вспомогательные плоскости частного положения и вспомогательные сферы, при этом следует стремиться к тому, чтобы фигуры сечения поверхностей посредниками по возможности были наиболее простыми — окружностями, прямоугольниками, прямыми линиями (рис. 1б).
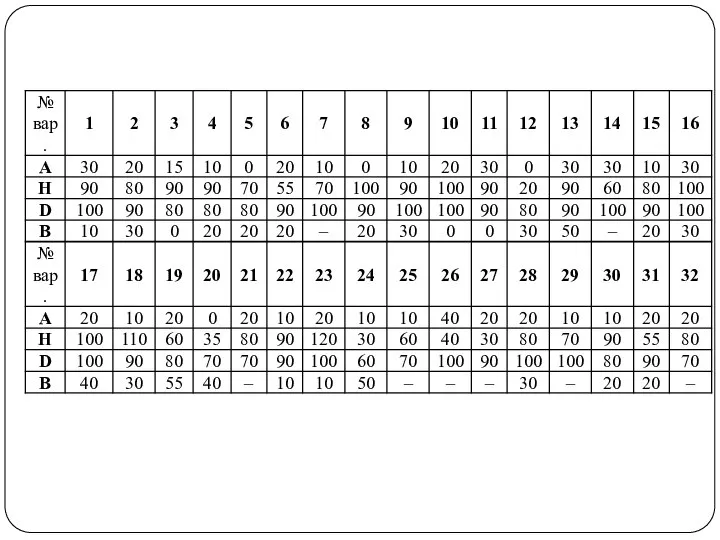
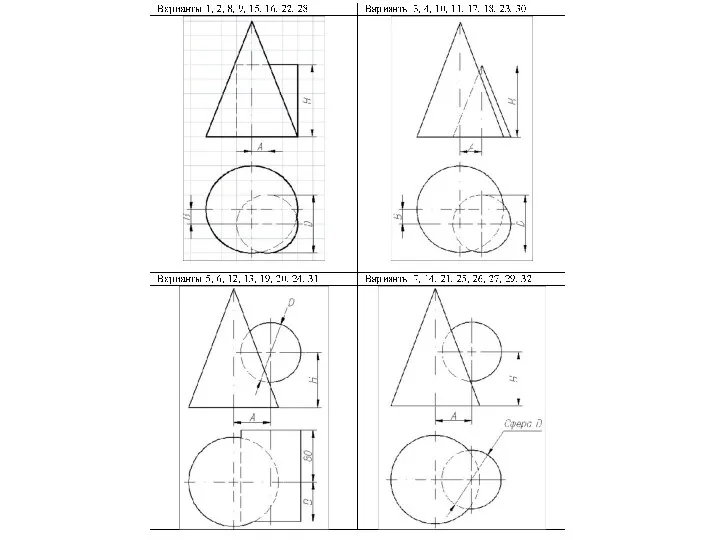
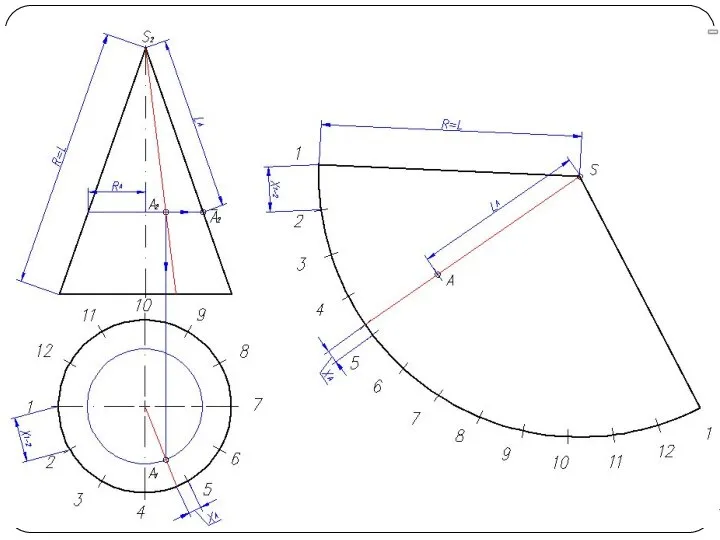
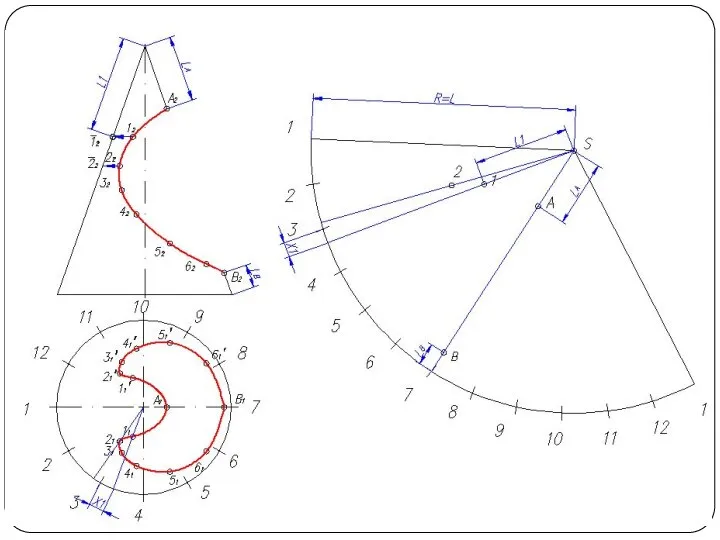
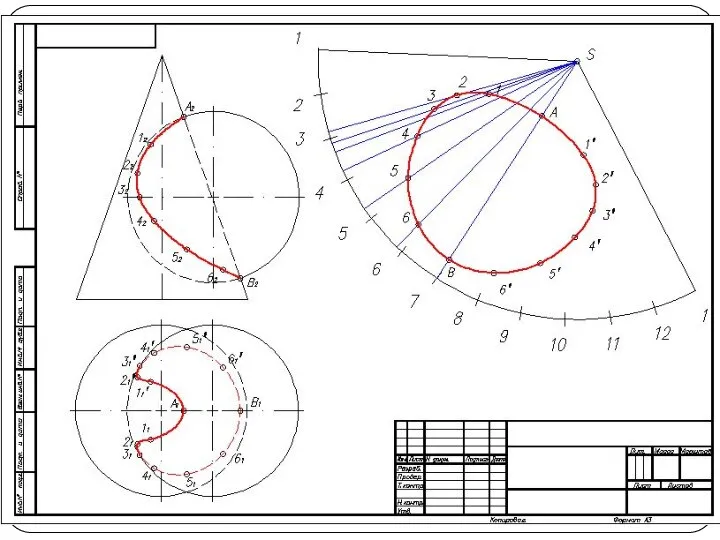
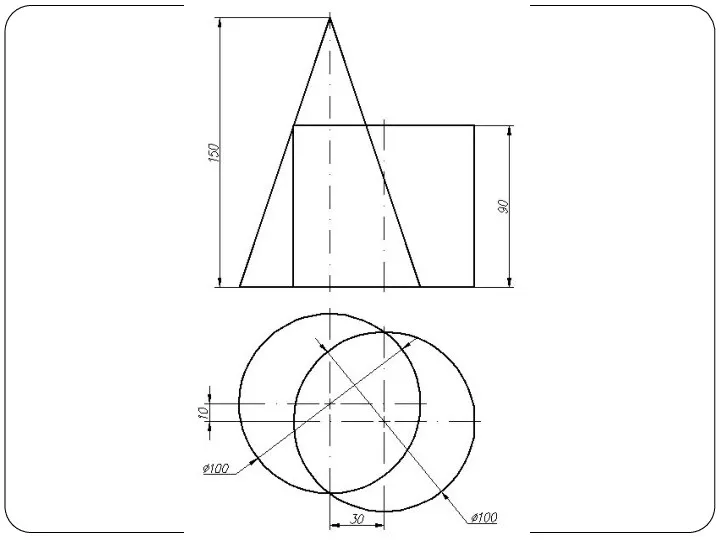
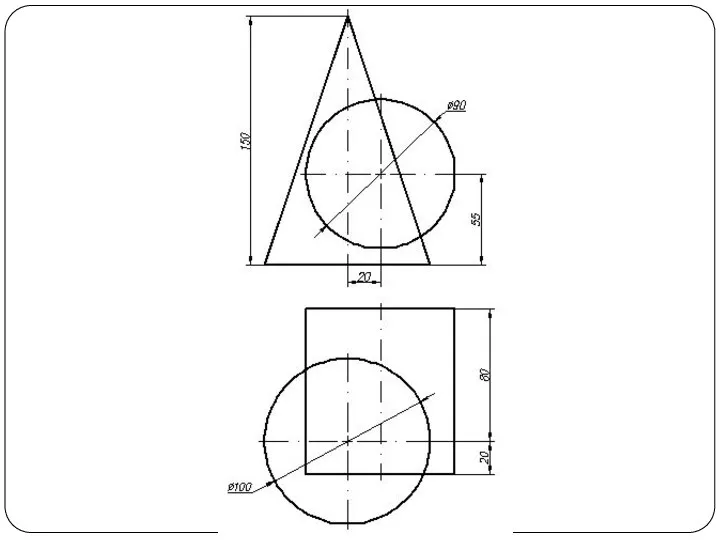
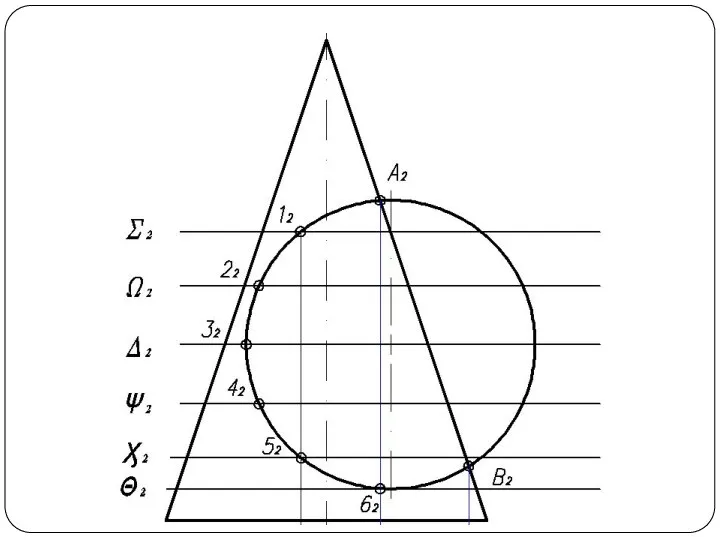
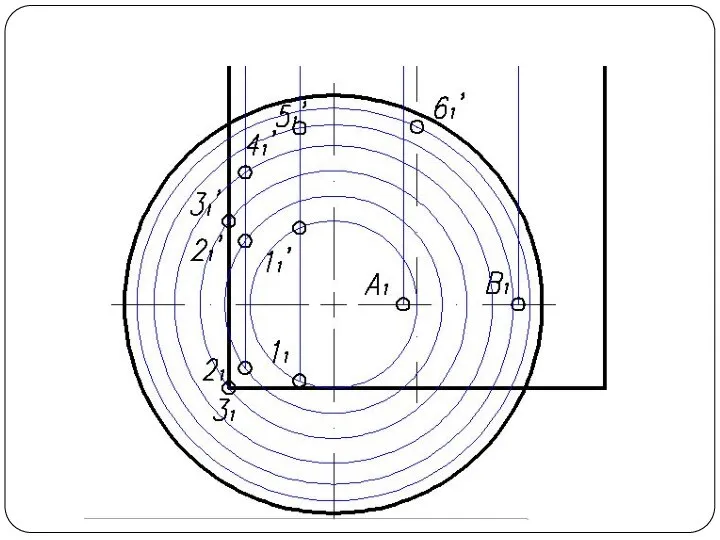
Слайд 5Построить линию пересечения поверхности прямого кругового конуса (диаметр основания – 100 мм,

высота – 150 мм) с заданной поверхностью вращения. Определить видимость, вычертить развертку конуса с нанесением линии пересечения. Задание выполнить по вариантам, приведенным в табл. 1.
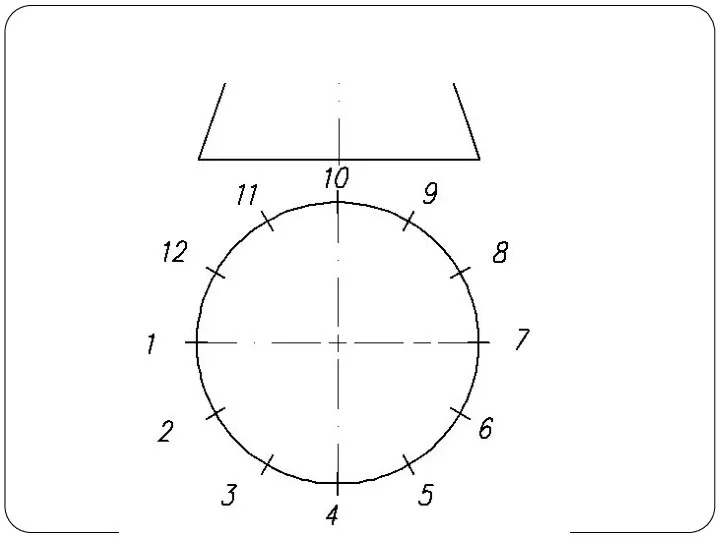
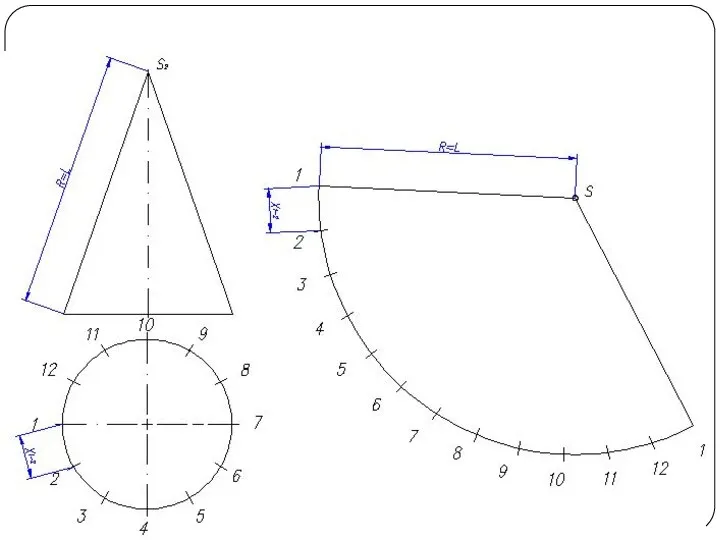
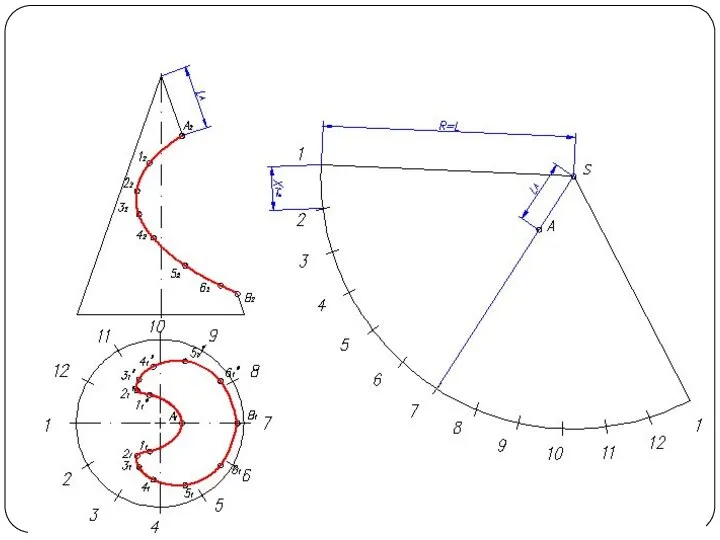
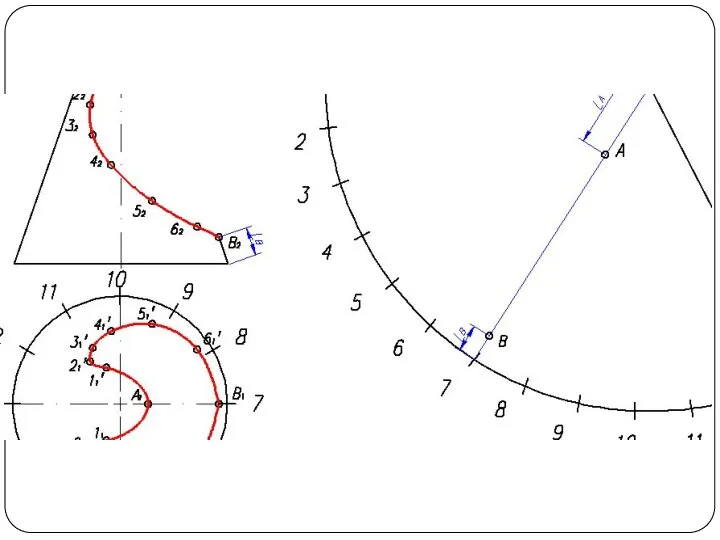
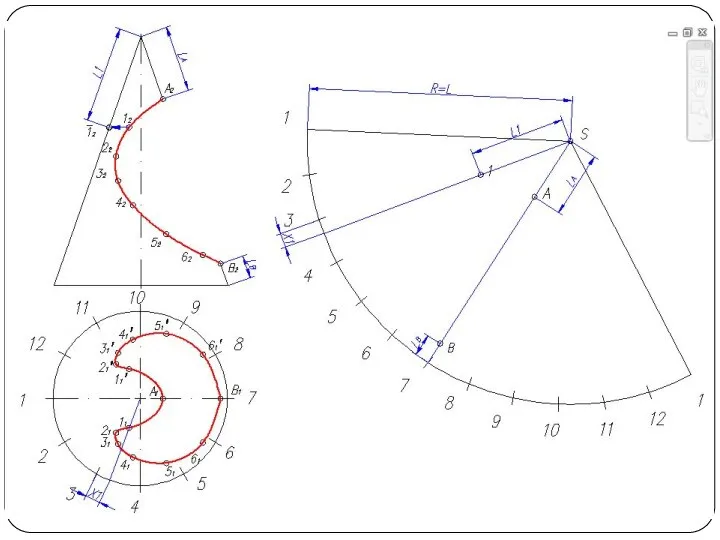
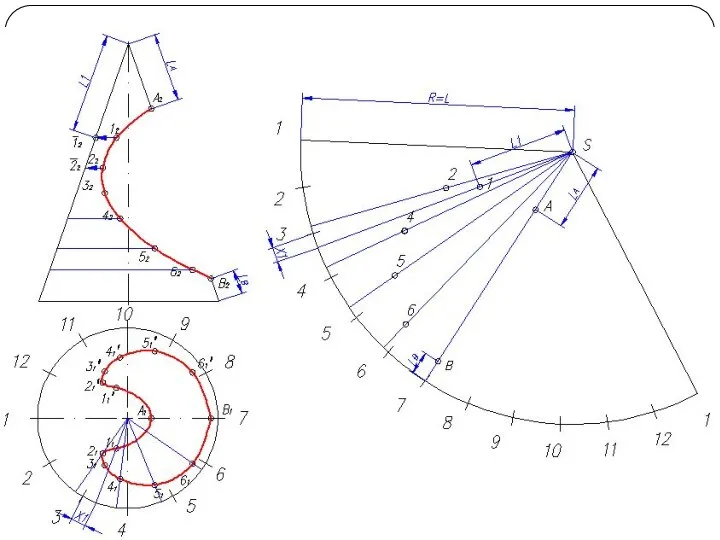
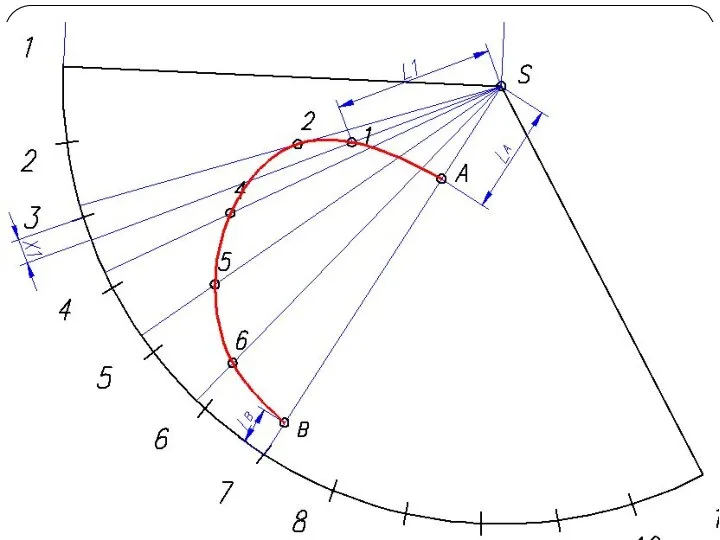
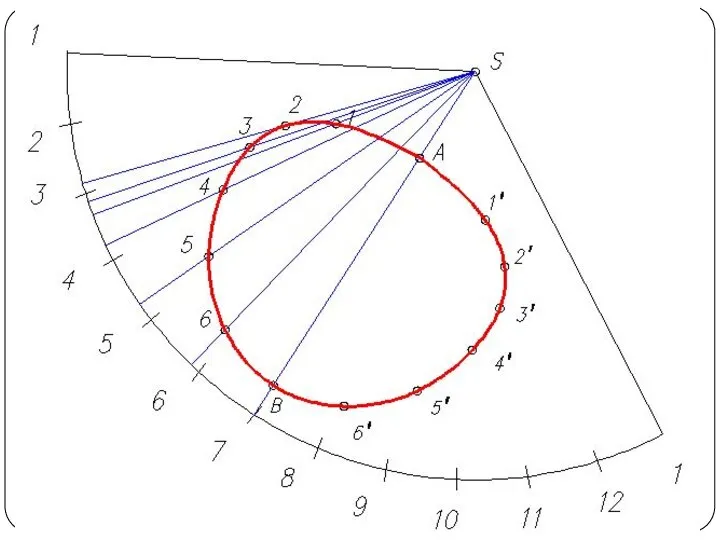
Слайд 26Построение развертки конуса
Разверткой называется плоская фигура, полученная совмещением поверхности тела с плоскостью.

Основной метод графического построения разверток - это аппроксимация заданной поверхности в виде многогранной поверхности
Часто в поверхность конуса вписывают многогранник с гранями в виде треугольников. Данный способ называется способом триангуляции
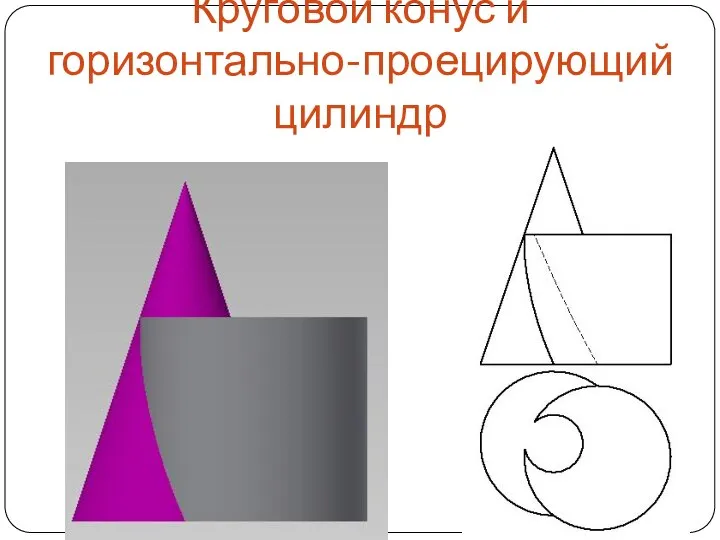
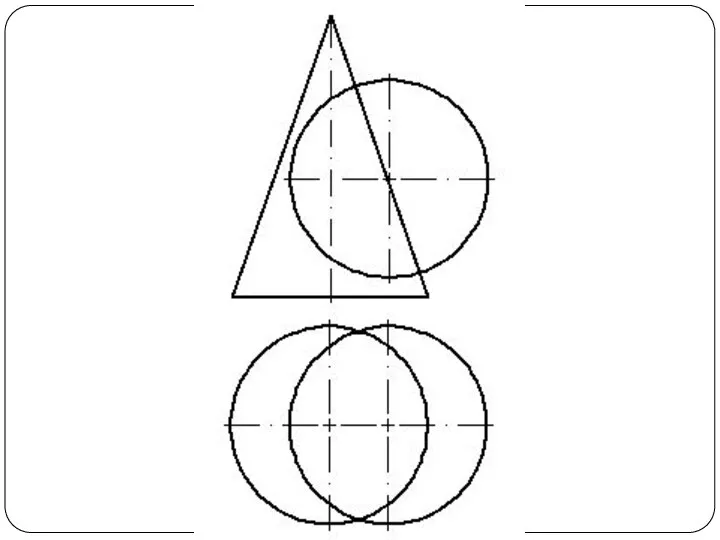
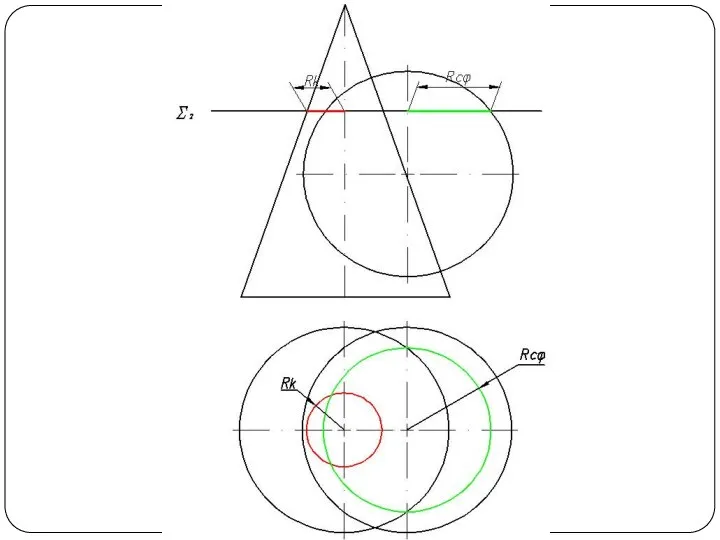
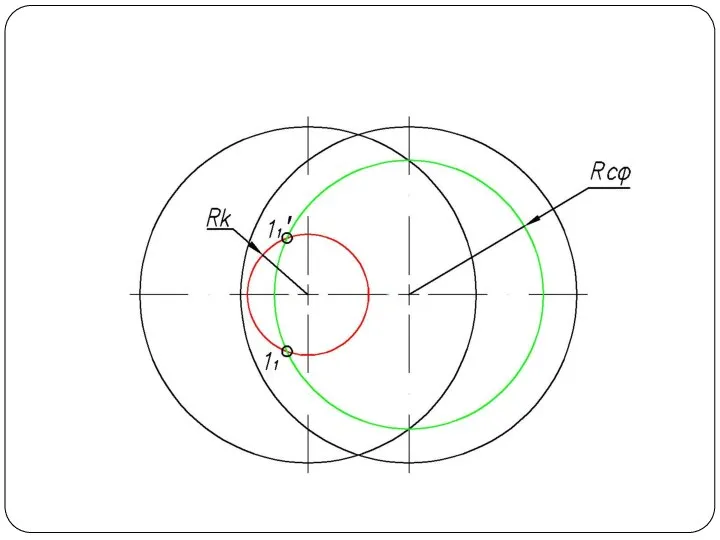
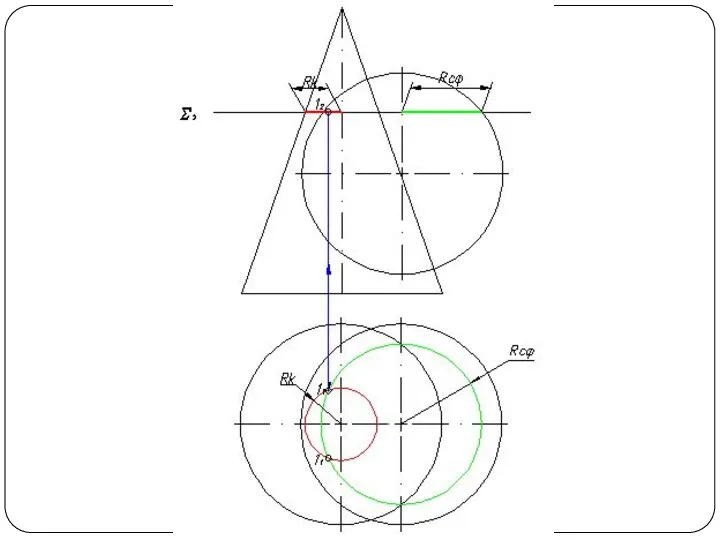
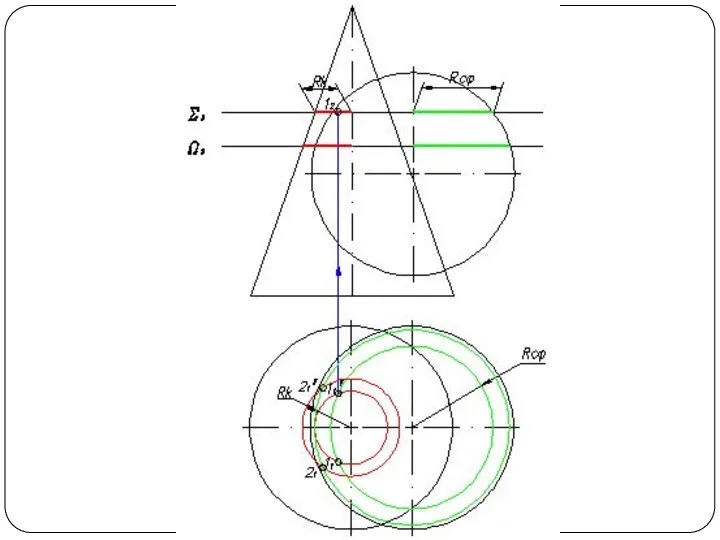
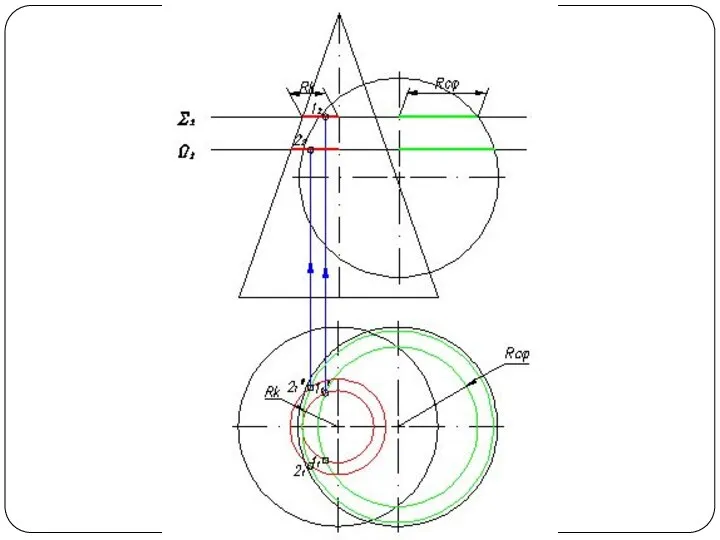
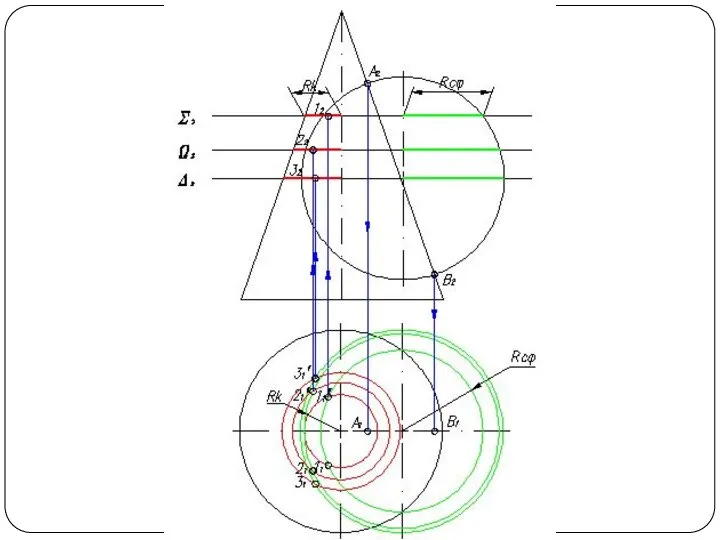
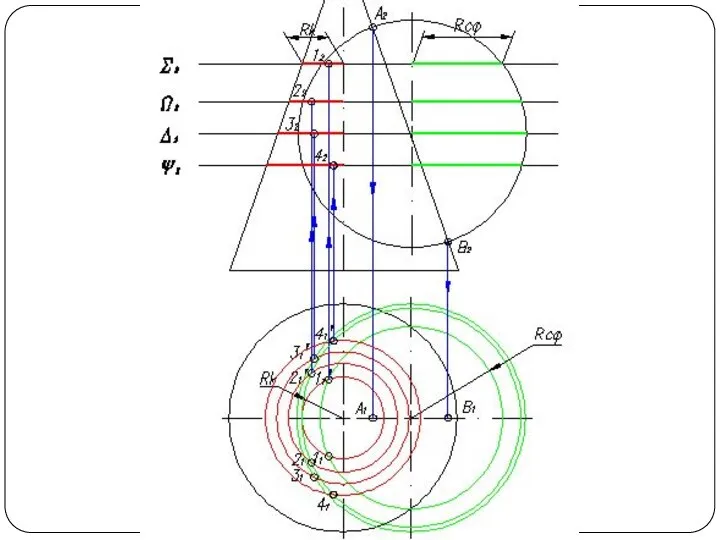
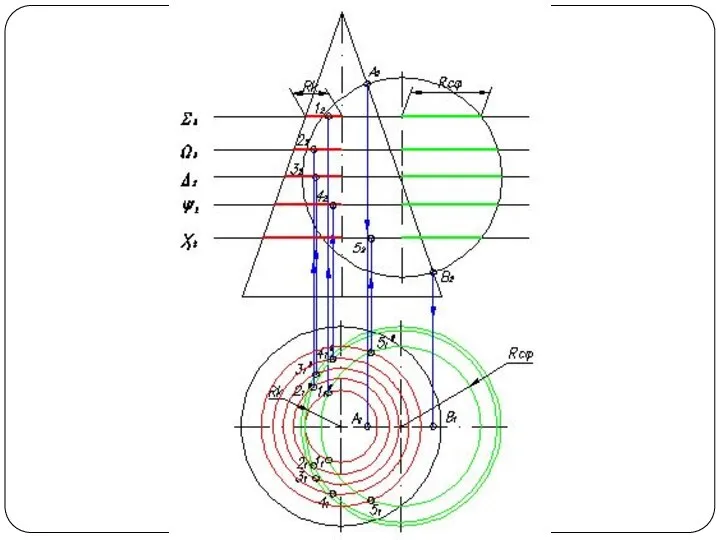
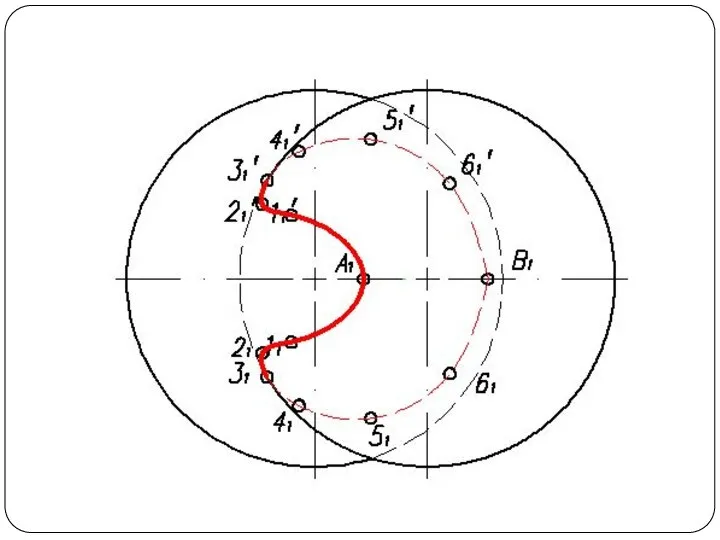
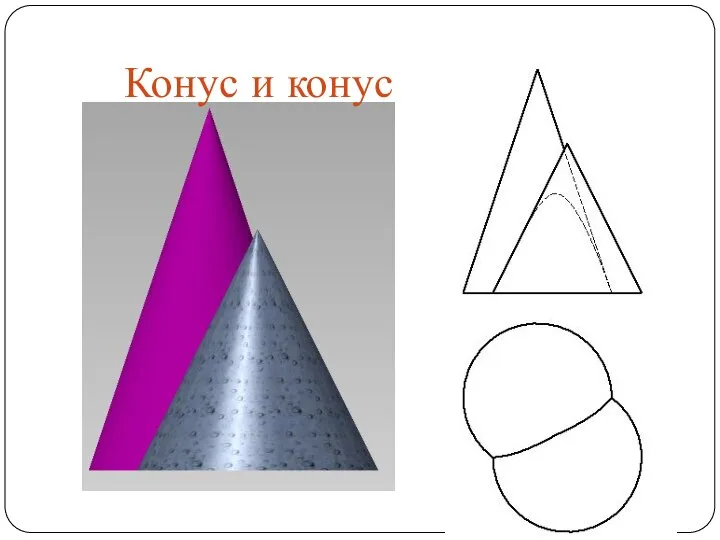
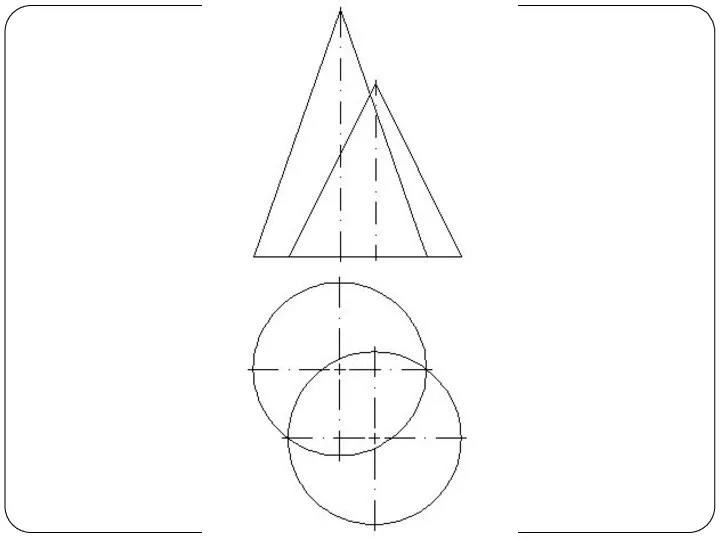
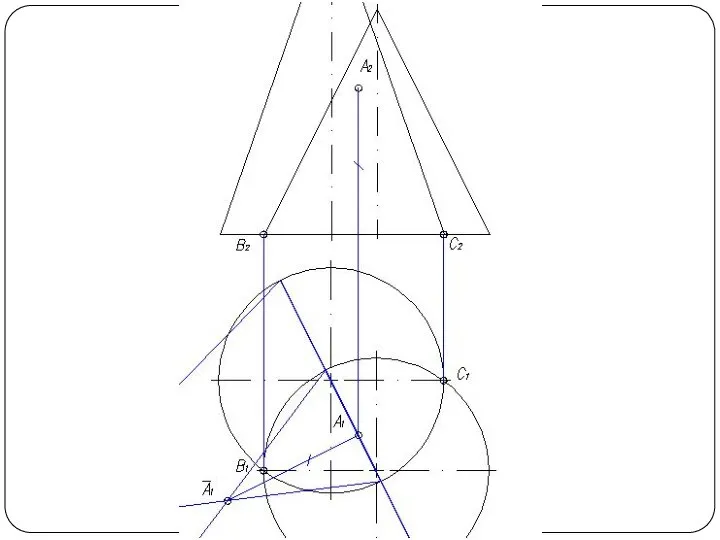
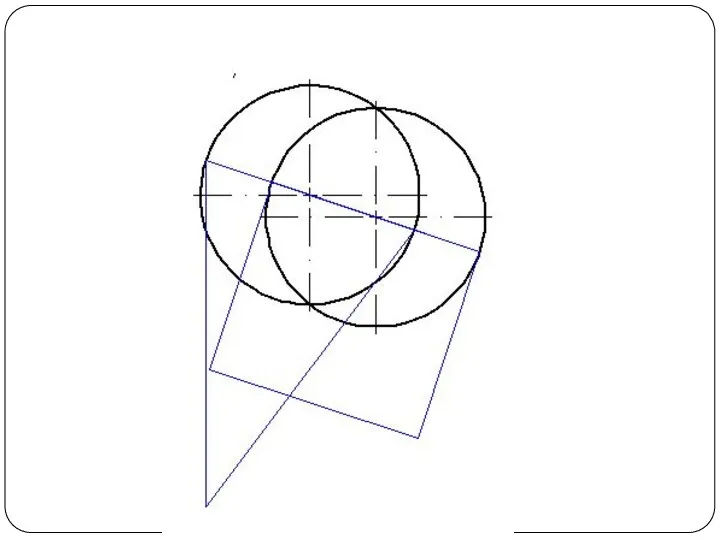
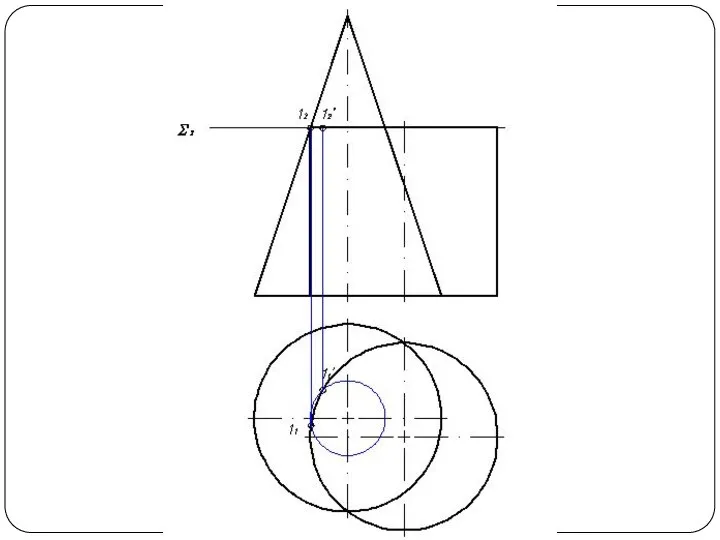
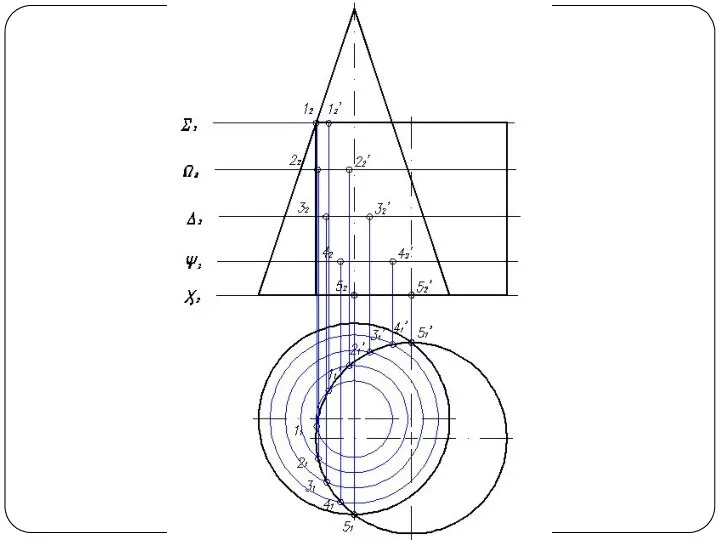
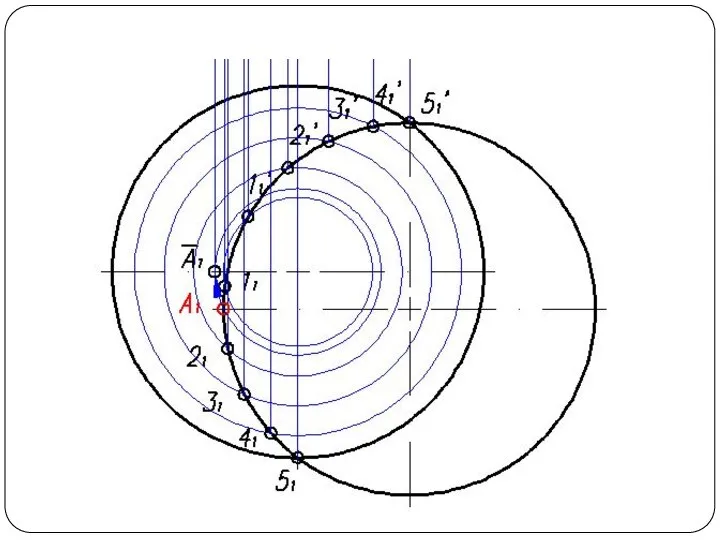
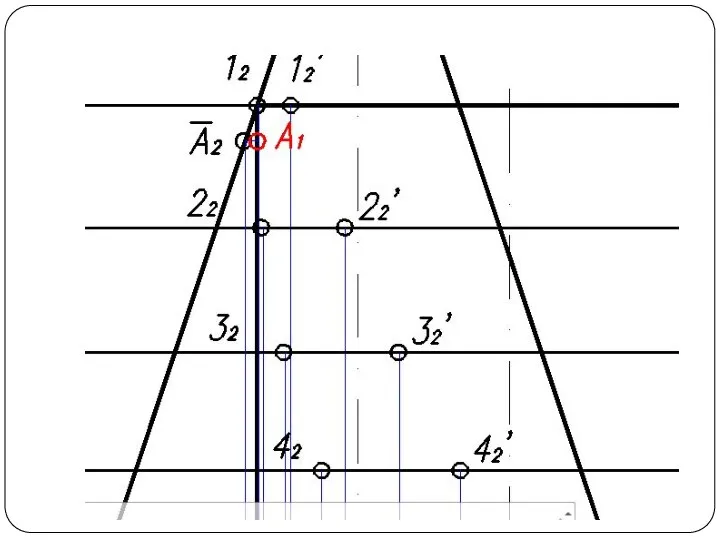
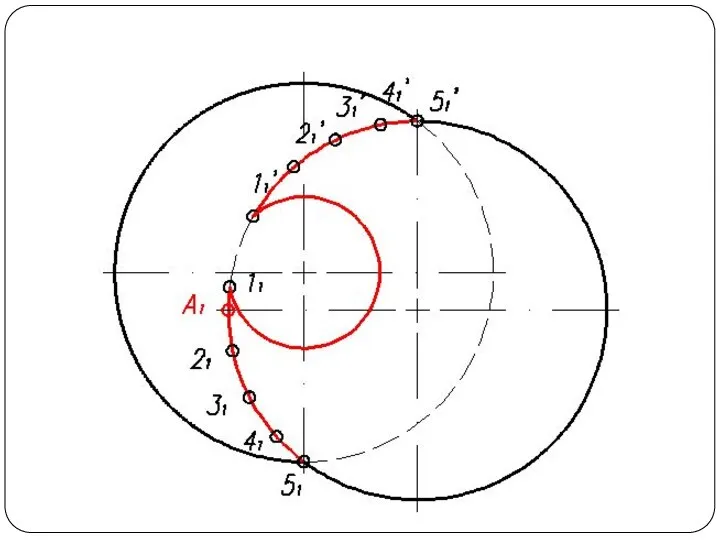
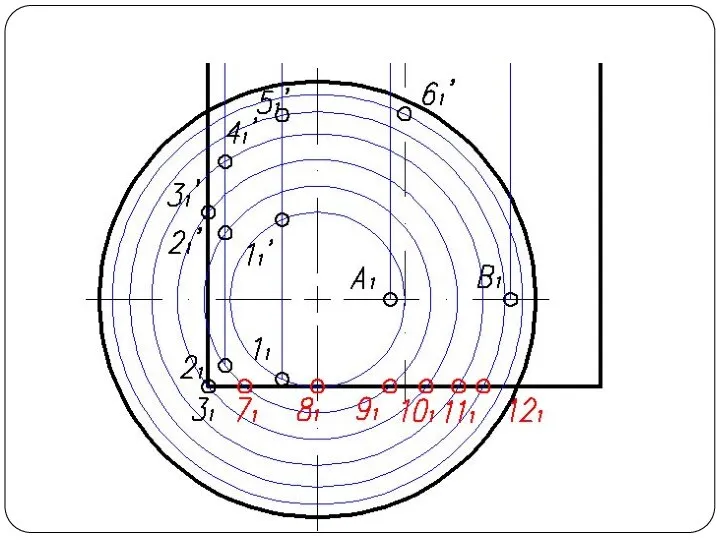
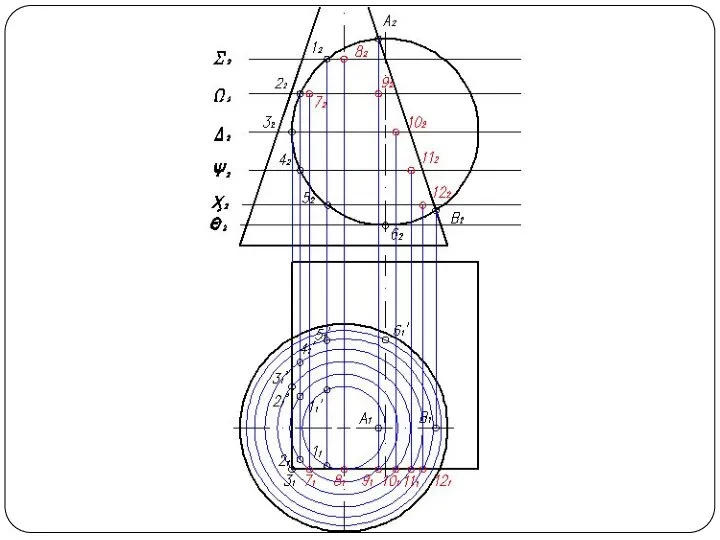
Слайд 48Круговой конус и горизонтально-проецирующий цилиндр
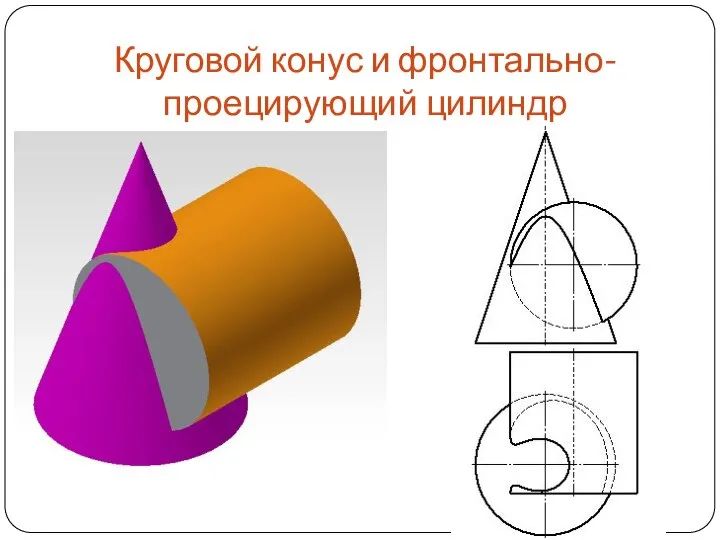
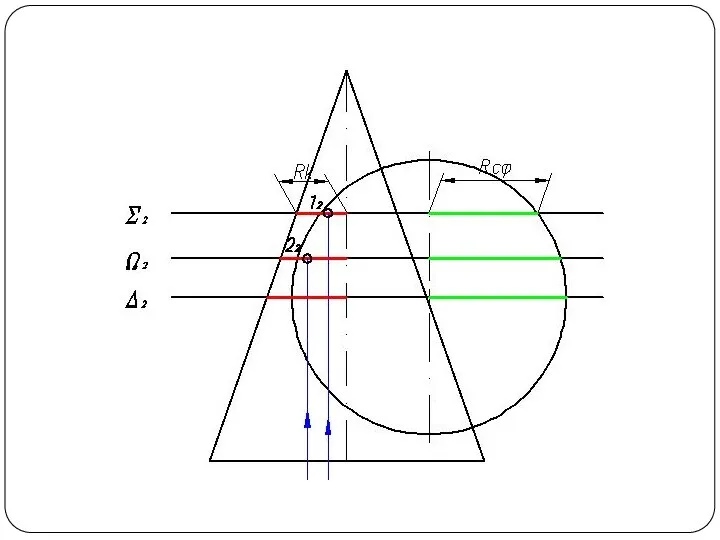
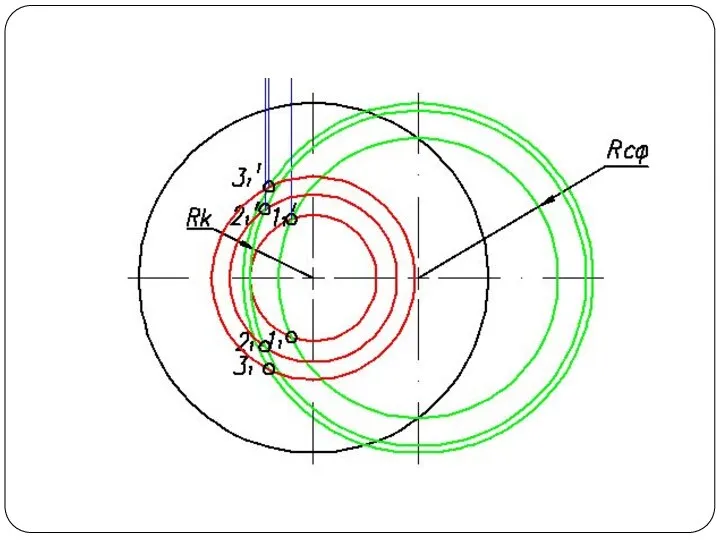
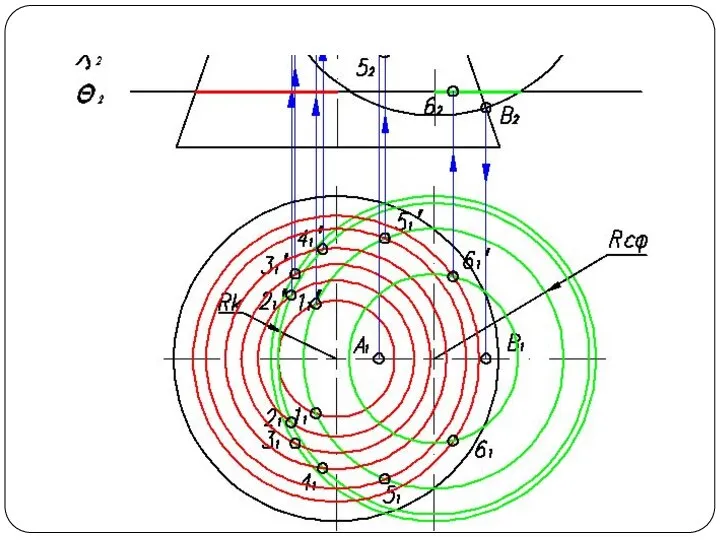
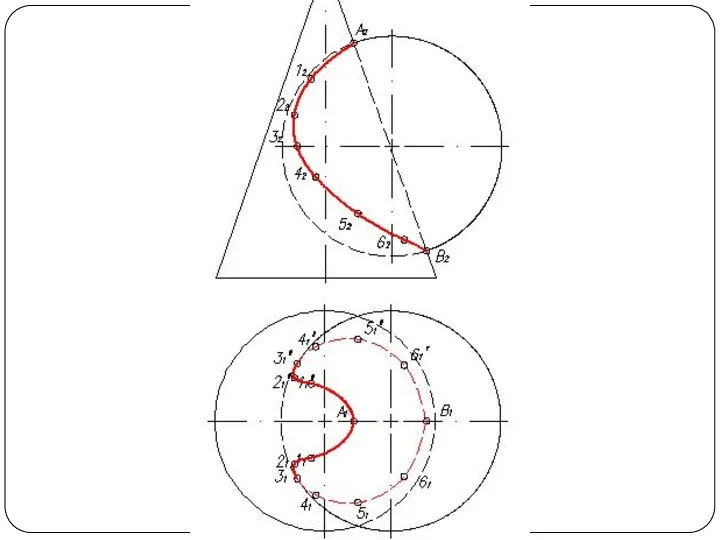
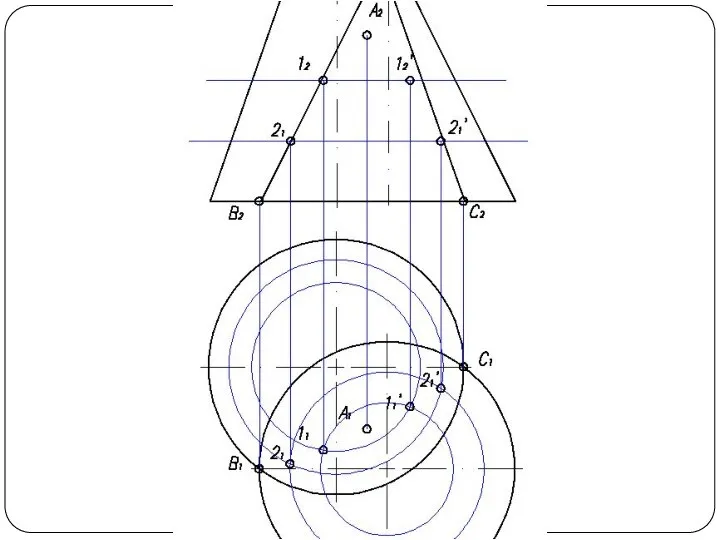
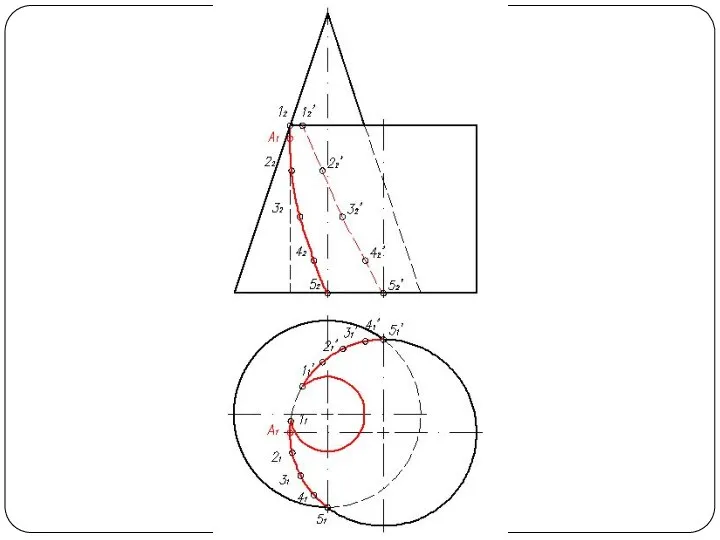
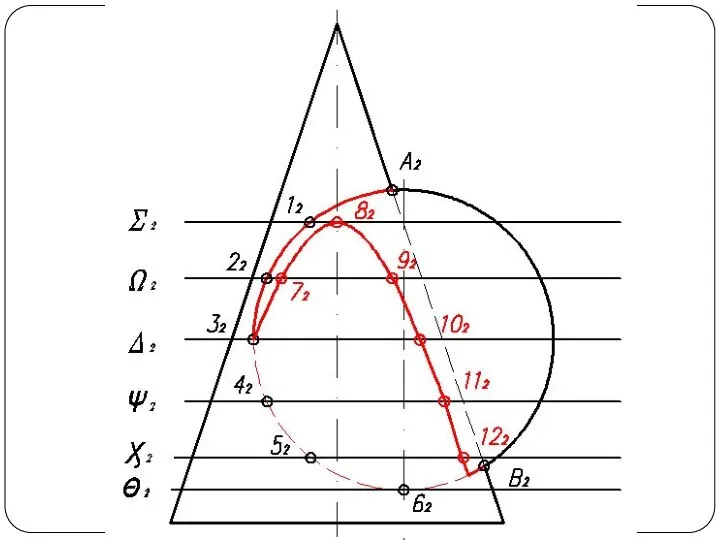
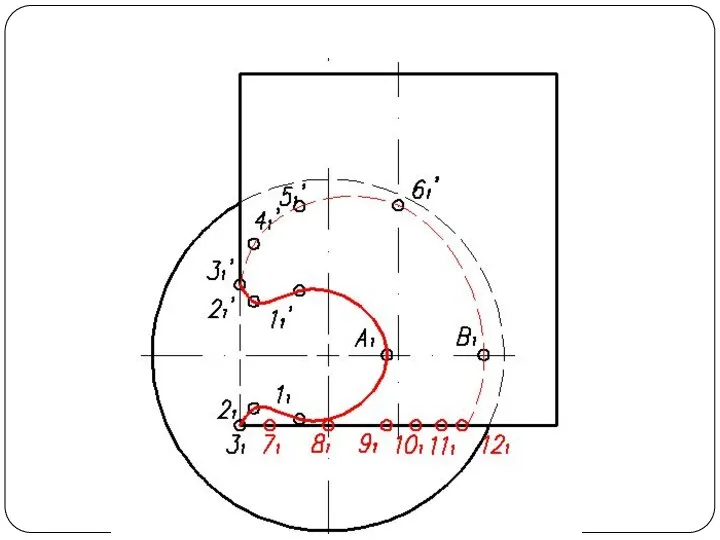
Слайд 57Круговой конус и фронтально-проецирующий цилиндр








 Удивительный мир симметрии
Удивительный мир симметрии Презентация на тему Одаренный ребенок» - кто он
Презентация на тему Одаренный ребенок» - кто он (Характеристика поэзии «шестидесятников»).
(Характеристика поэзии «шестидесятников»). Реклама для оптовых клиентов на бесплатной основе
Реклама для оптовых клиентов на бесплатной основе «Сертификация и лицензирование event-деятельности» Спикер: Щиголев Станислав Юрьевич. Владелец и Генеральный продюсер Агентства Ме
«Сертификация и лицензирование event-деятельности» Спикер: Щиголев Станислав Юрьевич. Владелец и Генеральный продюсер Агентства Ме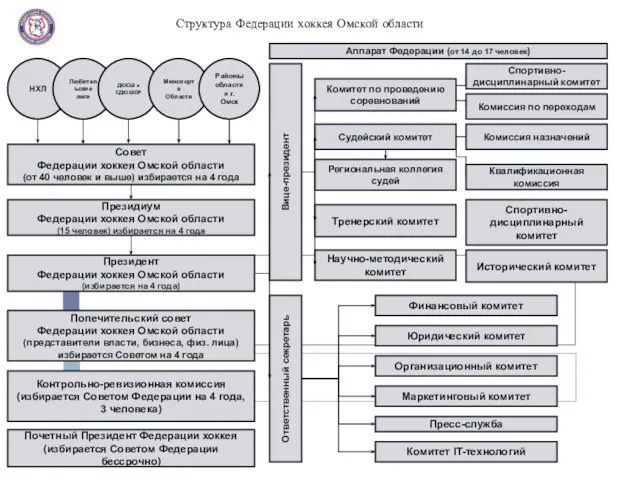 Структура Федерации хоккея Омской области
Структура Федерации хоккея Омской области LEXICAL PROBLEMS OF TRANSLATION
LEXICAL PROBLEMS OF TRANSLATION Ресурсы Мирового океана
Ресурсы Мирового океана Трудные времена для Руси!
Трудные времена для Руси! Президентская программа повышения квалификации инженерных кадров на 2012 -2014 гг.
Президентская программа повышения квалификации инженерных кадров на 2012 -2014 гг. Дивергентное мышление
Дивергентное мышление Государство и право России в период становления и развития абсолютной монархии (конец XVII – XVIII в.)
Государство и право России в период становления и развития абсолютной монархии (конец XVII – XVIII в.) Технобонус
Технобонус Когнитивные технологии и интеллект
Когнитивные технологии и интеллект Техногене серидовище 6 кл. (3)
Техногене серидовище 6 кл. (3) Деловое платье - признак хорошего чувства стиля.
Деловое платье - признак хорошего чувства стиля. Интернет-магазин рекламных материалов «1С-Битрикс»
Интернет-магазин рекламных материалов «1С-Битрикс» Права видавництв та їх працівників при проведенні перевірок щодо наявності неліцензійного програмного забезпечення Молотай Олександр юрист, керівник практики з інтелектуальної власності ТОВ “СіЕмЕс Камерон Маккена” Тел: +380 44 391 33 77 Факс: +3
Права видавництв та їх працівників при проведенні перевірок щодо наявності неліцензійного програмного забезпечення Молотай Олександр юрист, керівник практики з інтелектуальної власності ТОВ “СіЕмЕс Камерон Маккена” Тел: +380 44 391 33 77 Факс: +3 ОБЛІК НЕМАТЕРІАЛЬНИХ АКТИВІВ
ОБЛІК НЕМАТЕРІАЛЬНИХ АКТИВІВ Foreign languages in our life
Foreign languages in our life Магнитогорский технический колледж
Магнитогорский технический колледж Большой Театр
Большой Театр Толерантность
Толерантность Работа электрического тока
Работа электрического тока Лагерь с дневным пребыванием Я выбираю успех!
Лагерь с дневным пребыванием Я выбираю успех! Когда умрут аптечные сети?
Когда умрут аптечные сети? Ковроткачество
Ковроткачество Русская послевенчальная праздничная одежда
Русская послевенчальная праздничная одежда