Фильтры Колмогорова-Винера

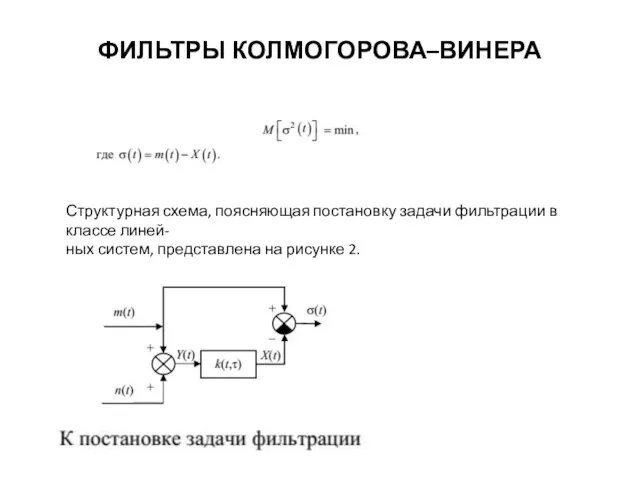
ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Рисунок 1 - К постановке задачи фильтрации

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Заданы взаимно некоррелированные центрированные нестационарные случайные
процессы в виде функций времени m t( ) и n t( ) с корреляционными функциями

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Требуется найти ИПФ k( t*, τ) фильтра, оптимальным образом выделяющего
реализацию случайного процесса m(t) в виде некоторого процесса X (t) в условиях,
когда на вход поступает аддитивная смесь полезного сигнала m(t) и помехи n(t).
Критерием оптимальности является минимум среднеквадратической ошибки (СКО)

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Структурная схема, поясняющая постановку задачи фильтрации в классе линей-
ных систем, представлена на рисунке 2.

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Найдем уравнение, определяющее ИПФ оптимальной, в указанном выше смысле,
системы. Положим, что при t = 0 фильтр имеет нулевые начальные условия; тогда
сигнал ошибки σ(t) определяется зависимостью

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
После осреднения по множеству получим
Для квадрата ошибки можно записать выражение

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Предположим, что
т.е. ИПФ k t( , τ) отличается от оптимальной ИПФ k( t*, τ) на некоторую функцию γΔ τk (t)

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Тогда из предыдущих двух формул следует

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Из предыдущей формулы следует, что для того, чтобы
необходимо выполнение условия

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Это условие легко получить, используя положение вариационного исчисления,
согласно которому необходимым условием экстремума функции
является соотношение
Подставляя (18) в (21), находим (20)

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Можно показать, что уравнение (3.20) является также и достаточным условием
минимума среднеквадратической ошибки. Действительно, поскольку
и, очевидно, функция
следовательно,
то так как
k t* ( ), τ действительно определяет фильтр, обеспечивающий минимальную СКО.
Перепишем (20) в виде

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Полученное интегральное уравнение 1-го рода (3.24) определяет оптимальную
ИПФ фильтра, обеспечивающего воспроизведение полезного сигнала m t( ) с минимальной СКО.
Уравнение (24) называется уравнением Винера–Хопфа, которое часто записывается в виде
(25)

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Для рассматриваемого случая уравнение Винера–Хопфа имеет вид
(26)

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Причем корреляционная функция сигнала, определяемая
по формуле
взаимная корреляционная функция сигнала на входе Y (t) и полезного входного сигнала m(t ).
Перепишем (26) в виде (после преобразования по Фурье)
(27)

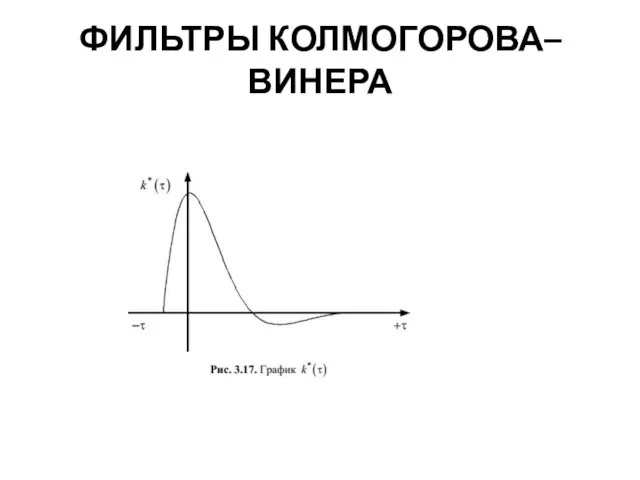
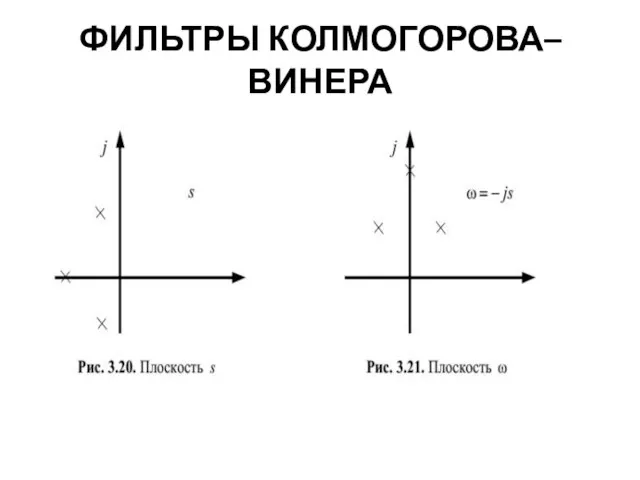
ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА
Оптимальная ИПФ, определяемая этой формулой, будет отлична от нуля для отрицательных значений τ (рис. 3.17)
Такая система физически нереализуема. Однако приближенное построение фильтра
возможно (рис. 3.18).

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА

ФИЛЬТРЫ КОЛМОГОРОВА–ВИНЕРА