Содержание
- 2. Историческая справка Открытие сверхпроводимости: 1911 г., Каммерлинг Оннес
- 3. Низкотемпературные измерения Т0 = 0 К = -2730С
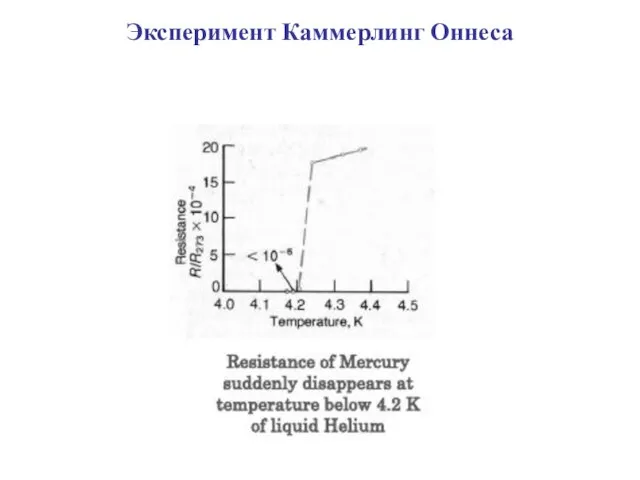
- 4. Эксперимент Каммерлинг Оннеса
- 5. 1. Основные экспериментальные факты
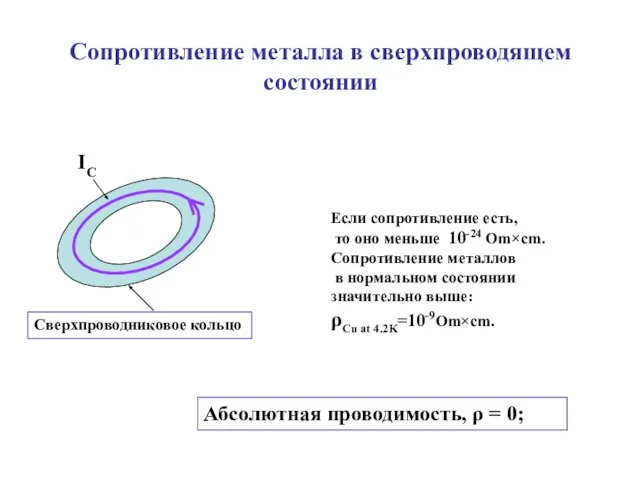
- 6. Сопротивление металла в сверхпроводящем состоянии IC Сверхпроводниковое кольцо Если сопротивление есть, то оно меньше 10-24 Оm×сm.
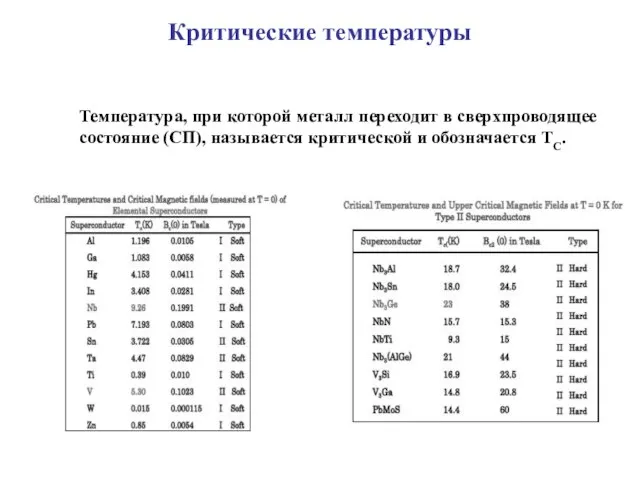
- 7. Критические температуры Температура, при которой металл переходит в сверхпроводящее состояние (СП), называется критической и обозначается ТС.
- 8. Сверхпроводник в магнитном поле СП состояние может быть разрушена определенным магнитным полем. Это поле называют критическим
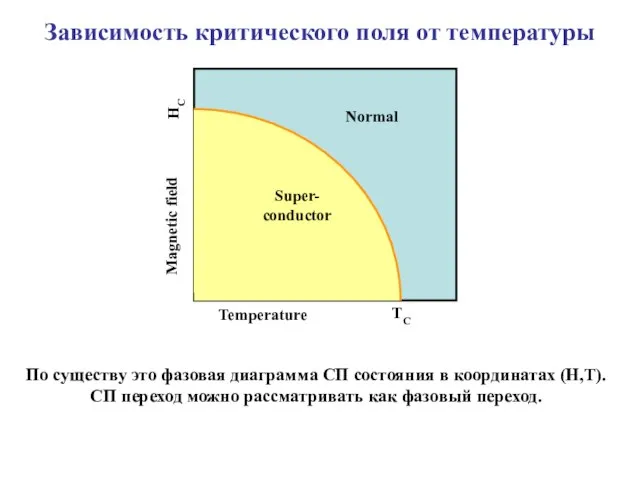
- 9. Зависимость критического поля от температуры Super- conductor Normal Temperature TC Magnetic field HC По существу это
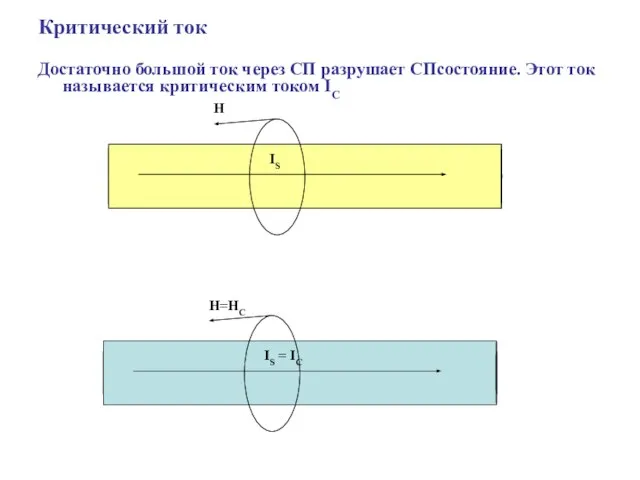
- 10. Критический ток Достаточно большой ток через СП разрушает СПсостояние. Этот ток называется критическим током IC IS
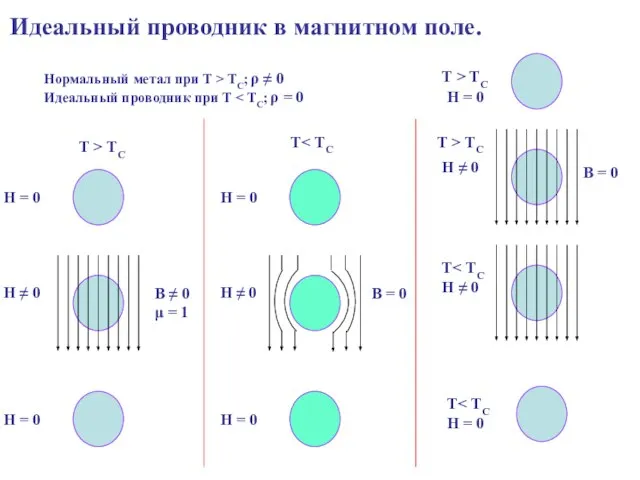
- 11. Идеальный проводник в магнитном поле. Нормальный метал при Т > TC; ρ ≠ 0 Идеальный проводник
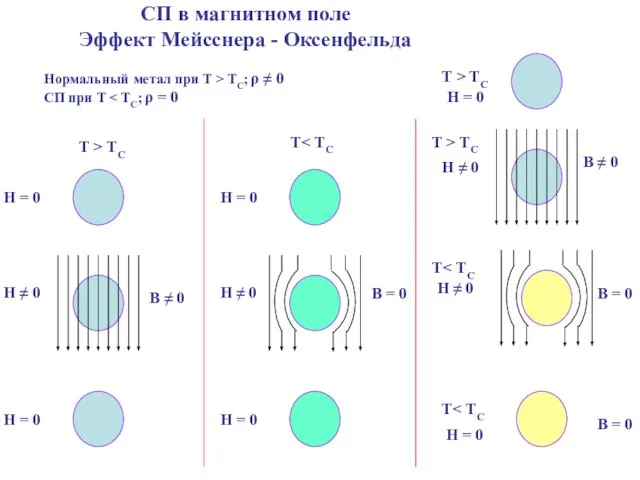
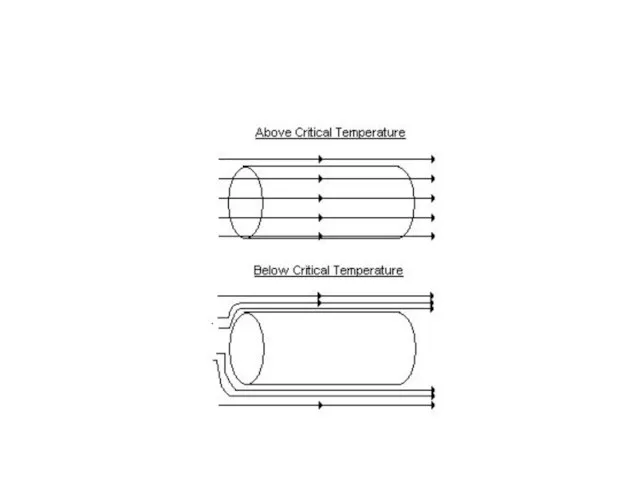
- 12. СП в магнитном поле Эффект Мейсснера - Оксенфельда Нормальный метал при Т > TC; ρ ≠
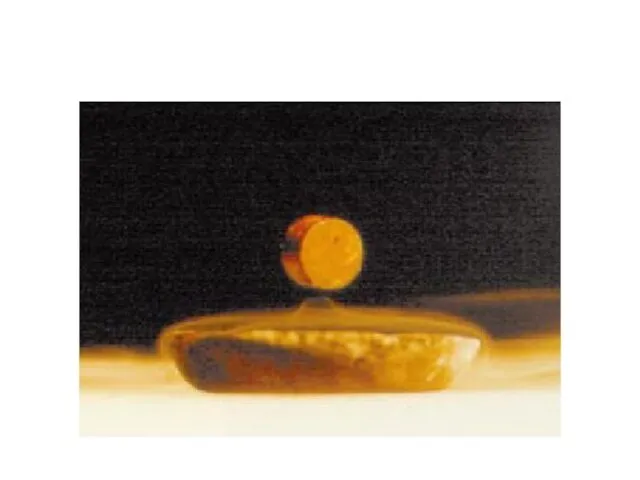
- 14. Левитация Сверхпроводники выталкивают магнитное поле, и поэтому отталкиваются от магнитов. Сила отталкивания может оказаться сильнее гравитации,
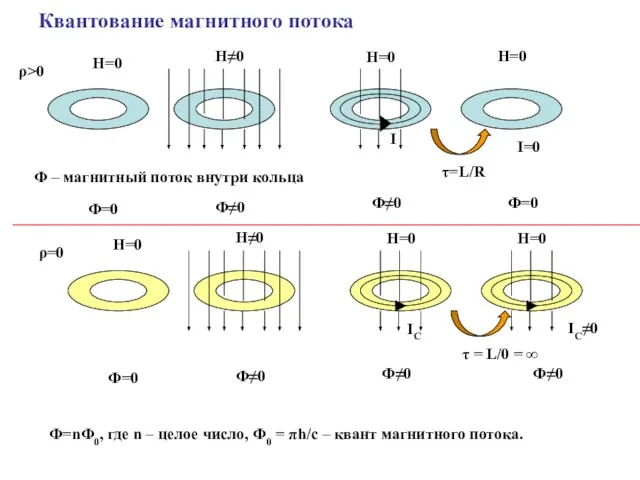
- 16. Квантование магнитного потока Н=0 Н≠0 Н=0 Н=0 Ф=0 Ф≠0 Ф≠0 Ф=0 τ=L/R ρ>0 Н=0 Н≠0 Н=0
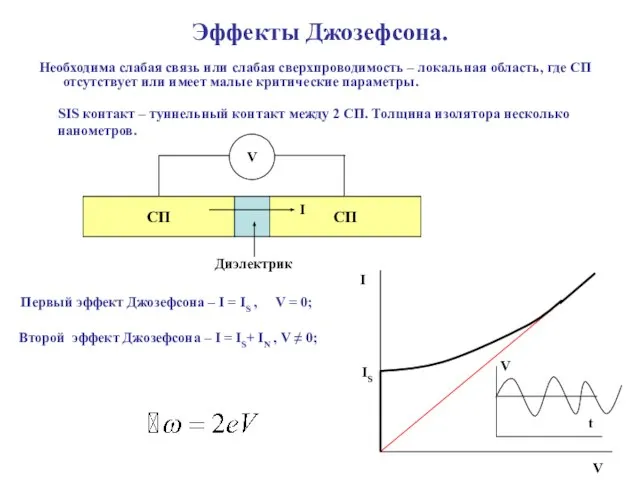
- 17. Эффекты Джозефсона. Необходима слабая связь или слабая сверхпроводимость – локальная область, где СП отсутствует или имеет
- 18. Магнитные свойства сверхпроводников СП отличаются по отклику на внешнее магнитное поле СП I рода Все элемент.СП
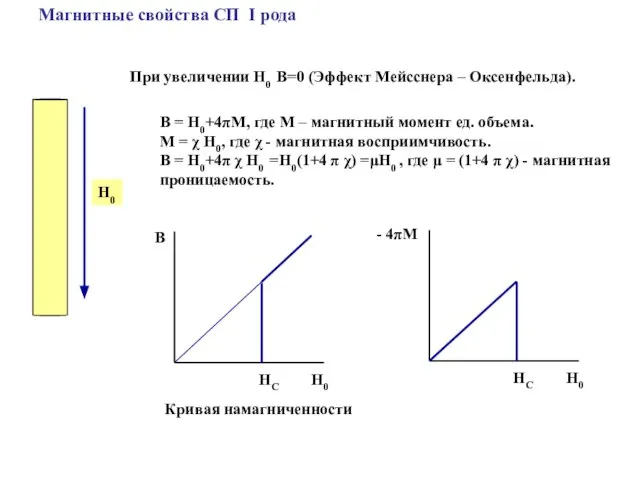
- 19. Магнитные свойства СП I рода При увеличении H0 В=0 (Эффект Мейсснера – Оксенфельда). H0 В HС
- 20. СП I рода Магнитные силовые линии вне СП всегда касательны к его поверхности. Линии вектора индукции
- 21. СП I рода По поверхности СП, находящегося в магнитном поле , всегда течет поверхностный электрический ток.
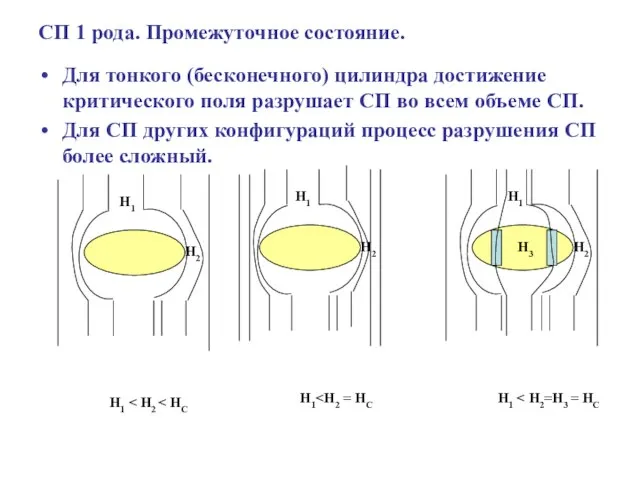
- 22. СП 1 рода. Промежуточное состояние. Для тонкого (бесконечного) цилиндра достижение критического поля разрушает СП во всем
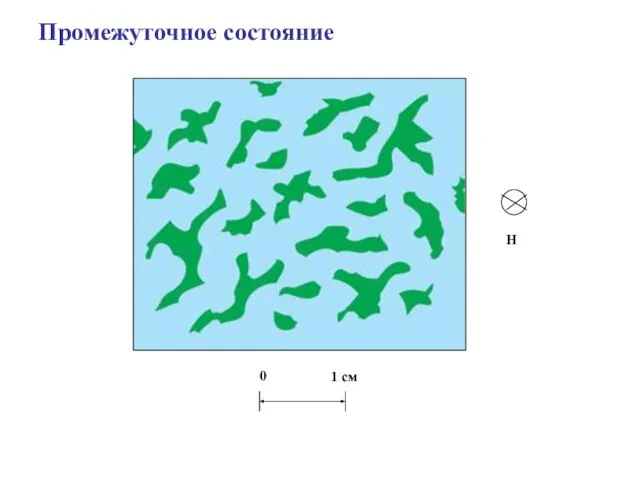
- 23. Промежуточное состояние H 0 1 см
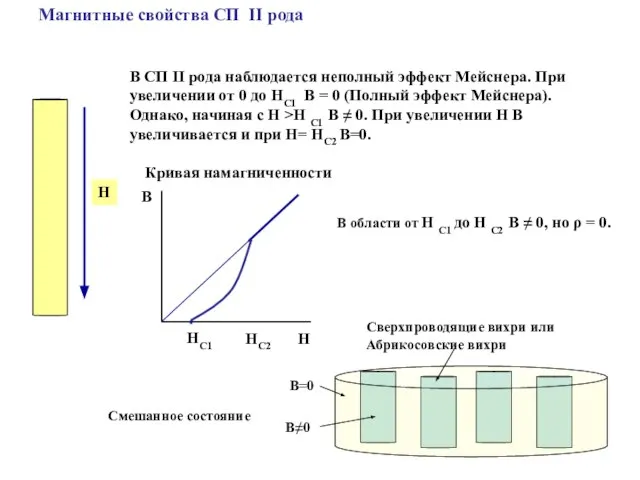
- 24. Магнитные свойства СП II рода В СП II рода наблюдается неполный эффект Мейснера. При увеличении от
- 25. Смешанное состояние, СП II рода Промежуточное состояние, СП I рода
- 26. 2. Термодинамика сверхпроводников
- 27. Критическое магнитное поле. Пусть Т Магнитный момент M единицы объема СП равен: M = -H0/4π Работа
- 28. Энтропия сверхпроводников. Согласно первому началу термодинамики где δQ – приращение плотности тепловой энергии рассматриваемого тела, δR
- 29. Из 2.7 следует 2.8 Воспользуемся формулой (3.10), чтобы вычислить разность удельных энтропии сверхпроводящего и нормального состояний.
- 30. Формула (2.9) позволяет получить важные физические следствия: Согласно теореме Нернста, энтропия всех тел при Т =
- 31. Мы можем сделать теперь весьма важные выводы. Оказывается, сверхпроводящее состояние является чем- то более упорядоченным, чем
- 32. Теплоемкость СП Теплоемкость нормального металла. Теплоемкость - это отношение тепла dQ, сообщенного телу, к изменению температуры
- 33. Электронная теплоемкость – квантовый подход. В 1928 году Зоммерфельд применил к электронам в металле квантовую статистику
- 36. Скачать презентацию


















 Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике
Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике England
England Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер»
Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер» Культура и традиции мордовского народа
Культура и традиции мордовского народа Почему нельзя не проветривать кабинет?
Почему нельзя не проветривать кабинет? Новый взгляд на экономическую географию
Новый взгляд на экономическую географию Презентация на тему Внутреннее строение млекопитающих
Презентация на тему Внутреннее строение млекопитающих Оживший Бог войны Арес - неукротимый бог войны
Оживший Бог войны Арес - неукротимый бог войны Гендерная статистика ЕГЭ по техническим предметам
Гендерная статистика ЕГЭ по техническим предметам Законы сохранения в механике
Законы сохранения в механике РДУ-99. Его значение и применение
РДУ-99. Его значение и применение India - English Transit
India - English Transit Презентация на тему Драгоценные камни
Презентация на тему Драгоценные камни 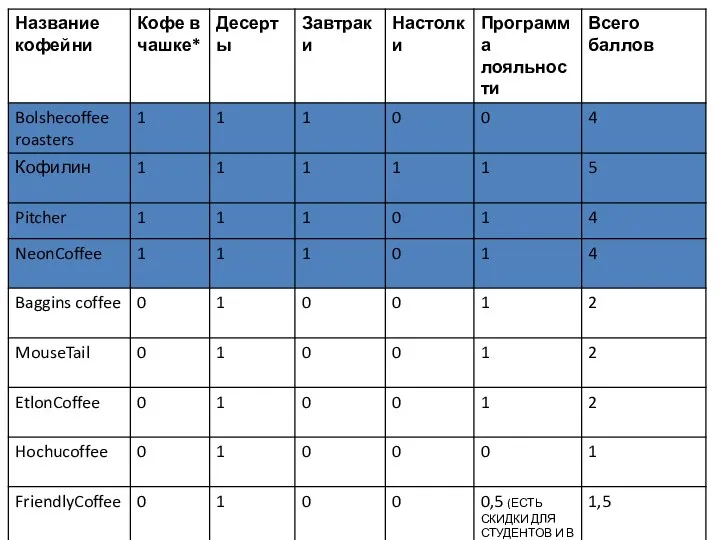 4. карта позиционирования, конкуренты_Шашина_3ГИВ13
4. карта позиционирования, конкуренты_Шашина_3ГИВ13 Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов
Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн
Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн Конкурс среди молодых семей «Семь Я»
Конкурс среди молодых семей «Семь Я» Ваше название
Ваше название Изготовление аксессуара Цветок
Изготовление аксессуара Цветок Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений
Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ»
Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ» Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения
Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения Специальность «Режиссер шоу-программ и театрализованных представлений»
Специальность «Режиссер шоу-программ и театрализованных представлений» Врачебный диагноз
Врачебный диагноз Привлечение средств от приносящей доход деятельности
Привлечение средств от приносящей доход деятельности Кукольный театр
Кукольный театр Большой, красивый, уютный.
Большой, красивый, уютный. Париж
Париж