Содержание
- 2. Pn(k)=Ckn pk(1-p)n-k Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pn(k) того,
- 3. Историческая справка ЯКОБ БЕРНУЛЛИ (1654–1705) Дата рождения: 27 декабря 1654г. Место рождения: Базель Дата смерти: 16
- 4. Пример использования формулы Бернулли Каждый день акции корпорации АВС поднимаются в цене или падают в цене
- 5. Проверь себя В урне 20 белых и 10 черных шаров. Вынули подряд 4 шара, причем каждый
- 6. Проверь себя Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2
- 7. Вероятность извлечения белого шара p=20/30=2/3 можно считать одной и той же во всех испытаниях; 1-p=1/3 Используя
- 8. РЕШЕНИЕ ЗАДАЧИ 2 Событие состоит в том, что из 4 фирм-нарушителей будет выявлено три или четыре,
- 9. Пусть А - появление 6 очков в одном испытании. Событие А в каждом из четырех независимых
- 10. РЕШЕНИЕ ЗАДАЧИ 4 Искомая вероятность равна сумме вероятностей трех событий, состоящих в том, что герб не
- 11. РЕШЕНИЕ ЗАДАЧИ 5 Известно, что P=0,9, по формуле Бернулли рассчитаем искомую вероятность: P7(5)=C57 0,95 (1-0,9)2 =21∙0,59049∙0,01=0,124
- 13. Скачать презентацию










 Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза Redaktiruemy_beydzh
Redaktiruemy_beydzh Физкультура. Виды плаванья
Физкультура. Виды плаванья О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС
О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС Письмо пером - за и против
Письмо пером - за и против Tin cup design
Tin cup design Транспорт. Виды транспорта
Транспорт. Виды транспорта Новый стандарт: обучаем и учимся
Новый стандарт: обучаем и учимся Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации
Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации Виды рабочей одежды
Виды рабочей одежды Я люблю тебя, Сакский район!
Я люблю тебя, Сакский район! Что такое значение?От П.Грайса к теории игр.
Что такое значение?От П.Грайса к теории игр. Тема лекции:«Прикладная информатика в табличном процессоре»
Тема лекции:«Прикладная информатика в табличном процессоре»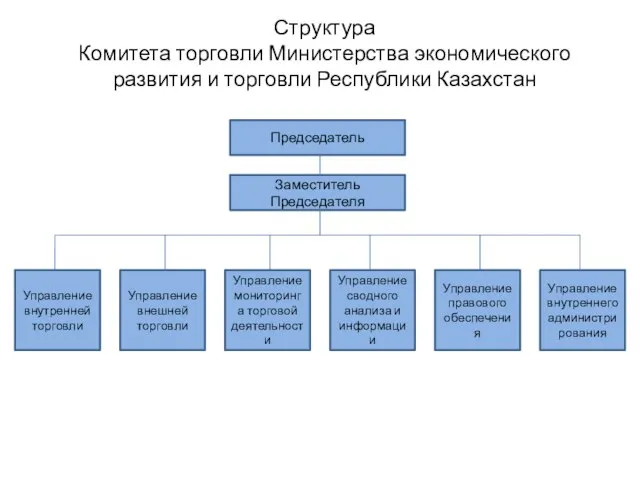 Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан
Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан Презентация на тему Информация в природе, обществе и технике
Презентация на тему Информация в природе, обществе и технике Основы коммуникативной компетентности педагогов
Основы коммуникативной компетентности педагогов Хочу отдыхать
Хочу отдыхать Урок по рассказам И.А. Бунина о любви
Урок по рассказам И.А. Бунина о любви Русская изба – поэтапное рисование
Русская изба – поэтапное рисование Известные люди Австрии
Известные люди Австрии 3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012
3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012 Викторина по произведениям А.П.Чехова « Смешные рассказы»
Викторина по произведениям А.П.Чехова « Смешные рассказы» Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г.
Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г. ЮТА (2)
ЮТА (2) Многообразие компьютеров
Многообразие компьютеров Похищение человека
Похищение человека Понятие и особенности административно правовой нормы
Понятие и особенности административно правовой нормы Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне