Формула Пика

Георг Пик
Георг Александр Пик (10 августа 1859 — 13 июля 1942) — австрийский математик, родился в еврейской семье.
Мать — Йозефа Шляйзингер. Отец — Адольф Йозеф Пик.

Образование и работы
Его обучал отец, возглавлявший частный институт
В 16 лет он окончил школу и поступил в Венский университет
В 20 лет получил право преподавать физику и математику
16 апреля 1880 года защитил докторскую диссертацию «О классе абелевых интегралов»
Им написано более 50 работ. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники

Преподавательская деятельность
В Немецком университете в Праге в 1888 году Пик получил место экстраординарного профессора математики, затем в 1892-м стал ординарным профессором. В 1900—1901 годах занимал пост декана философского факультета.
В 1910 году Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет.

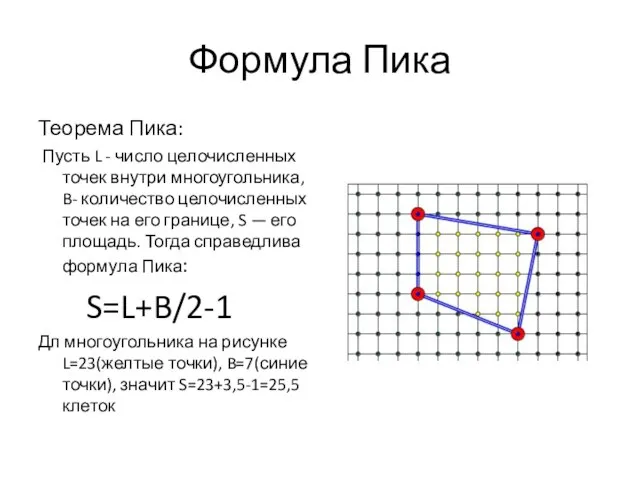
Формула Пика
Теорема Пика:
Пусть L - число целочисленных точек внутри многоугольника, B- количество целочисленных точек на его границе, S — его площадь. Тогда справедлива формула Пика:
S=L+B/2-1
Дл многоугольника на рисунке L=23(желтые точки), B=7(синие точки), значит S=23+3,5-1=25,5 клеток

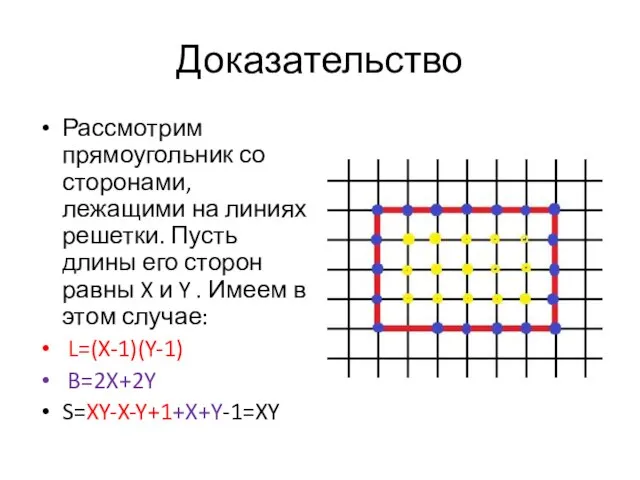
Доказательство
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны X и Y . Имеем в этом случае:
L=(X-1)(Y-1)
B=2X+2Y
S=XY-X-Y+1+X+Y-1=XY

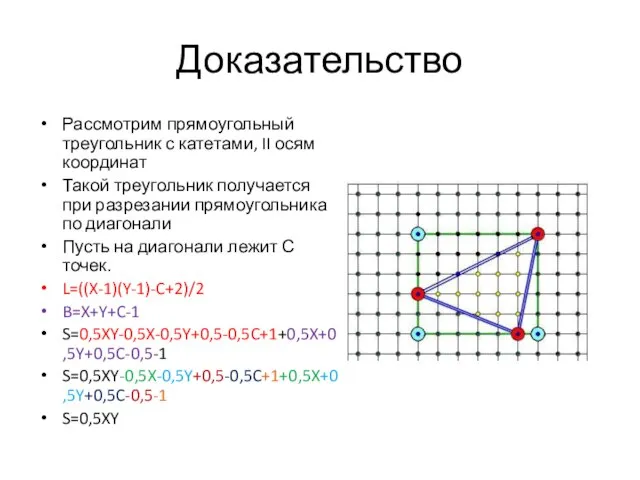
Доказательство
Рассмотрим прямоугольный треугольник с катетами, II осям координат
Такой треугольник получается при разрезании прямоугольника по диагонали
Пусть на диагонали лежит С точек.
L=((X-1)(Y-1)-C+2)/2
B=X+Y+C-1
S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1
S=0,5XY-0,5X-0,5Y+0,5-0,5C+1+0,5X+0,5Y+0,5C-0,5-1
S=0,5XY

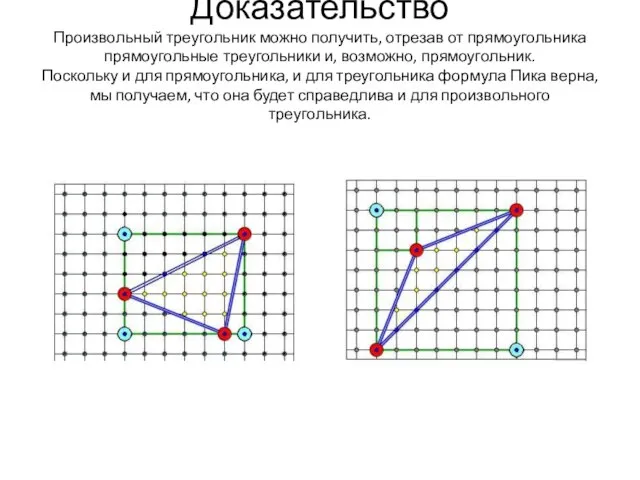
Доказательство
Произвольный треугольник можно получить, отрезав от прямоугольника прямоугольные треугольники и, возможно, прямоугольник.
Поскольку и для прямоугольника, и для треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Доказательство для многоугольника
Пусть многоугольник M и треугольник T имеют общую сторону. Предположим, что для M формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из M добавлением T. Так как M и T имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через c и получим
LMT=LM+LT+(c-2) — число внутренних целочисленных точек нового многоугольника,
BMT=BM+BT-2(c-2)-2 — число граничных точек нового многоугольника.
Из этих равенств получаем
LM+LP=LMT-(c-2),BM+BP=BMT+2(c-2)+2 .

Доказательство для многоугольника
Так как мы предположили, что теорема верна для M и для T по отдельности, то
SMT=SM+ST=(LM+BM/2-1)+(LT+BT/2-1)=
=(LM+LT)+(BM+BT)/2-2=
= LMT-(c-2)+(BMT+2(c-2)+2)/2-2=
=LMT+BMT/2-1 .
Тем самым, формула Пика доказана.

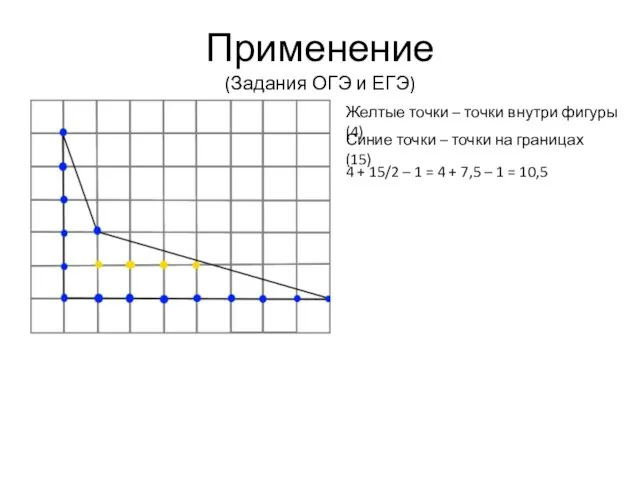
Применение
(Задания ОГЭ и ЕГЭ)
Желтые точки – точки внутри фигуры(4)
Синие точки – точки на границах(15)
4 + 15/2 – 1 = 4 + 7,5 – 1 = 10,5

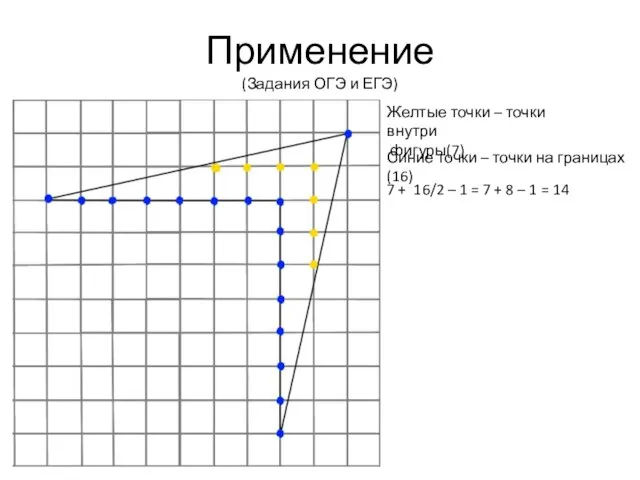
Применение
(Задания ОГЭ и ЕГЭ)
Желтые точки – точки внутри
фигуры(7)
Синие точки – точки на границах(16)
7 + 16/2 – 1 = 7 + 8 – 1 = 14