Фотонное эхо

Однородное и неоднородное уширение линий в спектрах
Имеется две причины ширин наблюдаемых линий в спектрах излучения:
1)Конечное время излучения приводит к лоренцевой форме линии излучения. Такое уширение называется однородным.
2) Разброс частот переходов разных излучателей. Это уширение называется неоднородным. Разброс частот для атомов в газе может быть связан с эффектом Доплера. В твердых телах с различием в окружении излучающего центра. Форма линии может быть гауссовой.

Динамика поляризации при неоднородном уширении
С хорошей точностью в классическом приближении электронные переходы можно рассматривать как колебания гармонического осциллятора. Пусть закон изменения поляризации для осциллятора с частотой ω имеет вид:
P(t)=P(0)exp(i ωt-t/T).
По какому закону будет изменяться во времени поляризация системы таких осцилляторов, которые имеют разные частоты?
В этом случае P(t)=P(0)∫exp(i ωt-t/T)g(ω)d ω.
Для простоты предположим, что частоты осцилляторов распределены по Лоренцу, т.е. вероятность найти осциллятор с частотой ω равна g(ω)= δ ω /π{(ω- ω0)2+δ ω2} . Пусть также времена затухания слабо отличаются.
Тогда P(t)=2P(0) δω exp(i ω0t- δ ω t-t/T)/(ω0-i δ ω );
В том случае когда δω>>1/T время затухания поляризации определяется величиной неоднородного уширения.
Для системы где g(ω)~exp{(ω- ω0)2/2(δω)2 }
P(t)~exp(iω0t- (δω)2t2/2-t/T)

Оптические уравнения Блоха
Рассматриваем двухуровневую систему. Электромагнитное поле описываем классически. Гамильтониан взаимодействия электрона с электромагнитным полем в электродипольном приближении имеет вид: -dE, d – оператор дипольного момента.
Уравнение для матрицы плотности имеет вид: dρ/dt=[H, ρ]/iћ+ St
Обозначим s1= ρ21+ ρ12=2Re(ρ12)
s2= -i(ρ12- ρ21)=2Im(ρ12)
s3=ρ22-ρ11
Можно проверить, что s12+s22+s32=1. Уравнения движения единичного вектора имеют вид:
ds/dt=[Ω s],
где Ω(-2drE/ ћ, -2diE/ ћ,ω21), ω21=(E2-E1)/ ћ
d12=dr+idi,

Движение псевдоспина
1. Нет внешнего поля. Прецессия вокруг оси 3 с частотой ω21. s3=const
s1=a cos(ω21t+δ)
s2=a sin(ω21t+δ)
Отметим что дипольный момент равен:
d(t)=drss+dis2 осциллирует с частотой ω21. – причина излучения системы.
2. Если внешнее поле отлично от нуля и E~cos(ωt), тогда удобно перейти во вращающуюся систему координат:
1
2
3
Тогда уравнение приобретает вид:
dρ/dt=[Ω’, ρ],
где Ω’(-2drEcos(ωt)/ ћ -2diEsin(ωt)/ ћ, -2diEcos(ωt)/ ћ +2drEsin(ωt)/ ћ,ω21-ω)

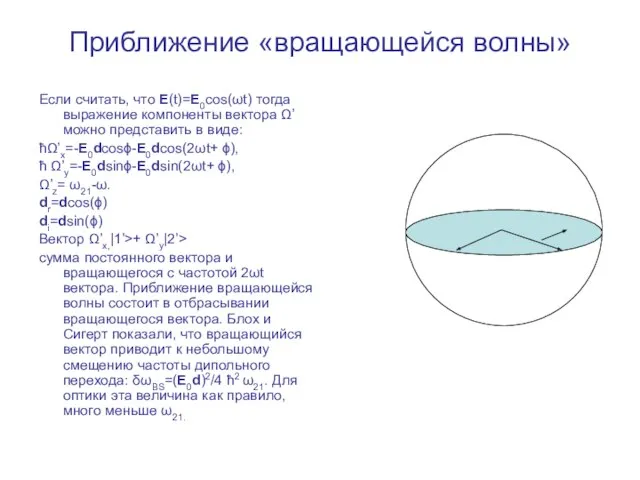
Приближение «вращающейся волны»
Если считать, что E(t)=E0cos(ωt) тогда выражение компоненты вектора Ω’ можно представить в виде:
ћΩ’x=-E0dcosϕ-E0dcos(2ωt+ ϕ),
ћ Ω’y=-E0dsinϕ-E0dsin(2ωt+ ϕ),
Ω’z= ω21-ω.
dr=dcos(ϕ)
di=dsin(ϕ)
Вектор Ω’x,|1’>+ Ω’y|2’>
сумма постоянного вектора и вращающегося с частотой 2ωt вектора. Приближение вращающейся волны состоит в отбрасывании вращающегося вектора. Блох и Сигерт показали, что вращающийся вектор приводит к небольшому смещению частоты дипольного перехода: δωBS=(E0d)2/4 ћ2 ω21. Для оптики эта величина как правило, много меньше ω21.

π - импульсы
Рассмотрим воздействие импульса излучения с ω= ω21 на систему в приближении вращающейся волны. В этом случае прецессия будет идти вокруг вектора, лежащего в плоскости (x,y). Можно выбрать разность фаз состояний так, чтобы di=0. В этом случае Ω’z= Ω’у=0, Ω’x=-. Вектор ρ прецессирует вокруг оси x с частотой E0dr/ћ – частота Раби.
При ∫dt E0dr/ћ=π вектор ρ повернется на π вокруг оси х. Такие импульсы называются π-импульсами.
В том случае, если частота внешнего поля немного не совпадает с частотой, тогда прецессия идет вокруг вектора (E0dr/ћ ,0, ω21-ω) с частотой [(E0dr/ћ)2+(ω21-ω)2]1/2, которая тоже называется частотой Раби.

Феноменологический учет затухания
Феноменологически затухание колебаний двухуровневой системы вводят следующим образом:
Для компонент 1,2 (x,y)
dρ1,2/dt=[Ω’, ρ]12-ρ12/T2, T2 – поперечное время жизни (время фазовой релаксации)
Для компоненты ρ3 :
dρ3/dt=[Ω’, ρ]3-(ρ3- ρ3равн)/T1,, T1 – продольное время жизни (время релаксации населенностей).
В отличие от классического диполя в двухуровневой системе имеется два времени релаксации.

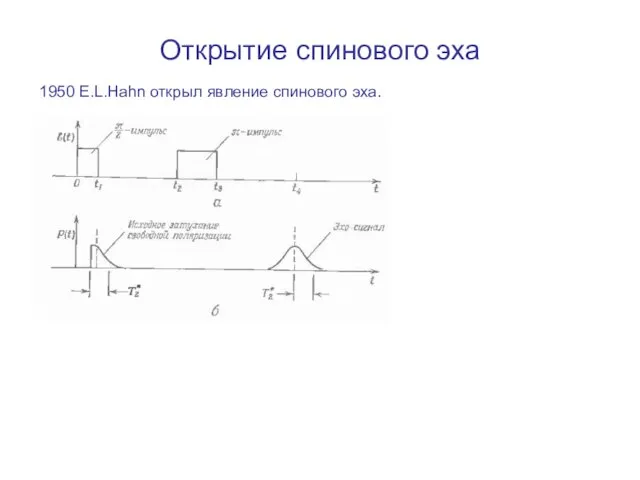
Открытие спинового эха
1950 E.L.Hahn открыл явление спинового эха.

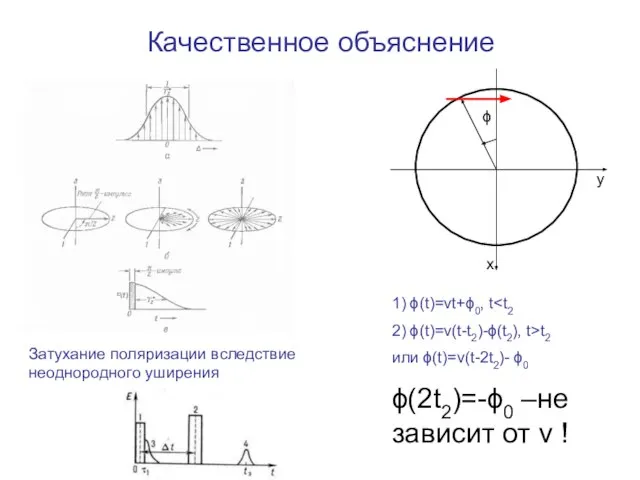
Качественное объяснение
Затухание поляризации вследствие неоднородного уширения
1) ϕ(t)=vt+ϕ0, t
2) ϕ(t)=v(t-t2)-ϕ(t2), t>t2
или ϕ(t)=v(t-2t2)- ϕ0
ϕ(2t2)=-ϕ0 –не зависит от v !
x
y

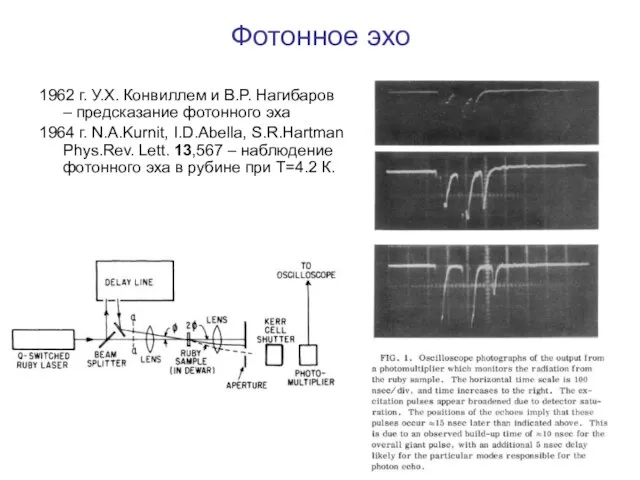
Фотонное эхо
1962 г. У.Х. Конвиллем и В.Р. Нагибаров – предсказание фотонного эха
1964 г. N.A.Kurnit, I.D.Abella, S.R.Hartman Phys.Rev. Lett. 13,567 – наблюдение фотонного эха в рубине при Т=4.2 К.

Направленность фотонного эха
В оптике длина образца как правило много больше длины волны. Поэтому диполи, возбуждаемые плоской волной, имеют разные фазы, если не находятся на фазовом фронте волны. Для вычисления поляризации необходимо усреднять не только по по расстройкам по частоте, но и по положению атомов. Это приводит к следующему выводу (см. Л.Аллен Дж. Эберли «Оптический резонанс и двухуровневые атомы»):
n1+n=2n2
n1- единичный вектор направления распространения π/2 импульса,
n2- единичный вектор направления распространения π импульса,
n- единичный вектор направления распространения эха
ϕ2<<λ/L