Содержание
- 2. Фракталы – геометрия природы Описание предмета фрактальной геометрии дал её создатель Бенуа Мандельброт в своей книге
- 3. Фрактальная размерность Понятие фрактал ввел в 1975 году французский ученый Бенуа Мандельброт для обозначения нерегулярных, но
- 4. Фракталы могут быть линейными и нелинейными. Линейные фракталы проявляют самоподобие в самом бесхитростном «прямолинейном» виде: любая
- 5. Бенуа Мандельброт Бенуа Мандельброт родился в Варшаве в 1924 году. В 1936 году его семья эмигрировала
- 6. Множество Мандельброта Наиболее сложный объект во всей математике – множество фрактальных форм Мандельброта. Чтобы рассмотреть множество
- 7. Фрактальные формы обнаруживаются не только в формах облака, гор, берегов морей, рек, озер, в дуновении ветра,
- 8. Человек нелинейный фрактал Хаос дал сильный толчок развитию теоретической биологии, объединив биологов и физиков в научные
- 9. Если физические функции организма правильно взаимодействуют друг с другом, значит, существует гармония в слаженной работе информационной
- 10. Заключение Хаос не нов, он существовал повсюду еще до появления времени и человечества. Мы – продукт
- 11. Универсальная методика На сегодняшний день абсолютно ясно, что необходима принципиально новая методика объективной помощи организму, позволяющая
- 12. Воздействие аппликаторами осуществляется до появления оздоровительного эффекта. Время экспозиции аппликаторов может колебаться в значительных пределах: от
- 13. Схема один.
- 14. Схема два
- 15. Схема три.
- 17. Скачать презентацию
Слайд 2Фракталы – геометрия природы
Описание предмета фрактальной геометрии дал её создатель Бенуа
Фракталы – геометрия природы
Описание предмета фрактальной геометрии дал её создатель Бенуа

Тема исследования: фракталы в биологии и медицине.
Цели исследования: анализ и роль фракталов в науке и медицине.
Объект исследования: фракталы, медицинские приборы на основе фракталов.
Задачи исследования:
научной литературы по исследуемому предмету;
Роль фракталов в медицине;
Изучение фрактальной организации объектов природы;
Презентация данного реферата средствами PowerPoint.
Структура работы;
Реферат состоит из введения, шести глав, заключения, списка литературы и приложения.
Презентация реферата на дискете.
Ричардсон обратил внимание, что при исследовании турбулентности (хаотических вихрей) воздушных потоков он обнаружил каскад энергии – от больших вихрей к малым, то есть своеобразную гармонию: маленькие вихри возникают внутри больших и как бы повторяют их форму и поведение.
А Заболоцкий искал в природе «разумную соразмерность», но представлял ее себе согласно классическим канонам – по Евклиду; а оказалось, что эта соразмерность имеет совершенно другую геометрию, о которой великий поэт не догадывался. Гармония есть и в недрах скал, и в пении ветров – причем везде она одна и та же.
Но более основано нам рассказывает о фракталах Бенуа Мандельброт.
Слайд 3Фрактальная размерность
Понятие фрактал ввел в 1975 году французский ученый Бенуа Мандельброт
Фрактальная размерность
Понятие фрактал ввел в 1975 году французский ученый Бенуа Мандельброт

”Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому”. Термин фрактал образован от латинского причастия fractus. Соответствующий глагол frangere переводится, как ломать, разламывать, т.е. создавать фрагменты неправильной формы.
Мандельброт объясняет сущность этого принципа на примере вычисления длины береговой линии или любой национальной границы. С феноменом береговой линии он столкнулся, изучив малоизвестную работу английского ученого Льюиса Ф. Ричардсона,
Береговая линия – представитель класса объектов, имеющих бесконечную длину в конечном пространстве. К таким объектам так же можно отнести снежинку Коха и коврик Серпинского.
Снежинка Коха
Коврик Серпинского
Слайд 4 Фракталы могут быть линейными и нелинейными. Линейные фракталы проявляют самоподобие в
Фракталы могут быть линейными и нелинейными. Линейные фракталы проявляют самоподобие в

Классическим примером фрактального объекта может служить канторовское множество или «пыль» Кантора.Аналогичным способом можно построить двухмерные геометрические объекты с размерностью между 1 и 2, и трехмерное с размерностью между 2 и 3. Например, размерность коврика Серпинского равна 1,58; снежинки Коха – 1,2618.
Мандельброт указал пути расчета дробных измерений объектов окружающей действительности. Создавая свою геометрию, он выдвинул закон о неупорядоченных формах, что встречаются в природы. Закон гласил: степень нестабильности постоянна при различных масштабах.
«Пыль» Кантора.
Слайд 5Бенуа Мандельброт
Бенуа Мандельброт родился в Варшаве в 1924 году. В 1936
Бенуа Мандельброт
Бенуа Мандельброт родился в Варшаве в 1924 году. В 1936

Сегодня Бенуа Мандельброт – профессор Йельского университета, член американской Академии искусств и наук и Национальной академии наук США. Он удостоен многочисленных почетных научных степеней и наград – премия Вольфа по физике.
Слайд 6Множество Мандельброта
Наиболее сложный объект во всей математике – множество фрактальных форм
Множество Мандельброта
Наиболее сложный объект во всей математике – множество фрактальных форм

Алгоритм Мандельброта позволяет получить как частный случай все множества Жюлиа. Если в итерационном процессе Zn+1Z2+C зафиксировать значение С и изменять Z0, то получится набор множеств Жюлиа. А если в итерационном процессе Zn+1Z2+C зафиксировать Z0 и изменять С, то получаем множество Мандельброта. Б. Мандельброт, открывший в 70-х годах ХХ века алгоритм Zn+1Z2+C, произвел с помощью ЭВМ множество итераций и получил график функции – эту удивительную фигуру, известную во всем мире под именем «фрактал Мандельброта».
Фрактал Мандельброта показан в двухмерном виде. Трех-мерный вид показал бы прекрасный мир спонтанности и свободы Множество Мандельброта – своеобразный каталог к бесконечному многообразию форм множества Жюлиа. Границы множества Мандельброта, поражающие своей сложностью и многообразием, включают в себя полный набор уменьшенных и деформированных копий множества Жюлиа. Множество Мандельброта – эффективное хранилище информации для бесконечного разнообразия множества Жюлиа.
Именно алгоритмом Мандельброта пользуется природа, создавая свои шедевры – фракталы золотого сечения – от листа травы до биологической популяции. Поэтому не удивительно, что фракталы поразительно красивы. Удивительная простота фрактальных алгоритмов и потрясающее великолепие их форм сделали фрактальную геометрию необычайно эффективным орудием для описания морфологических свойств природы. Не случайно говориться: «Мудрость в простоте». Принцип единого простого, задающего разнообразное сложное, можно проследить в устройстве всего мироздания.
Множество Мандельброта
Слайд 7 Фрактальные формы обнаруживаются не только в формах облака, гор, берегов морей,
Фрактальные формы обнаруживаются не только в формах облака, гор, берегов морей,
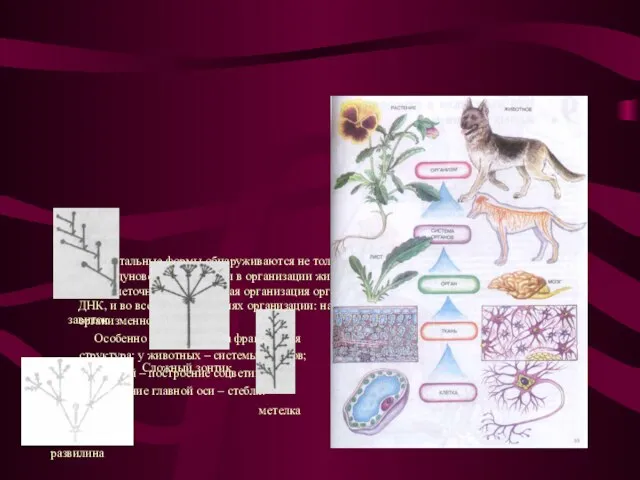
Особенно сильно заметна фрактальная
структура: у животных – системы органов;
у растений – построение соцветий,
разветвление главной оси – стебля.
Сложный зонтик
завиток
метелка
развилина
Слайд 8Человек нелинейный фрактал
Хаос дал сильный толчок развитию теоретической биологии, объединив биологов
Человек нелинейный фрактал
Хаос дал сильный толчок развитию теоретической биологии, объединив биологов

человека следует рассматривать как информационную структуру, пронизывающую физическое тело, которое представляет собой богатый источник нелинейных фракталов, причем, фракталов золотого сечения.
Нелинейными фрактальными структурами являются также все системы и органы человека. Так, например, кровеносные сосуды, начиная от аорты и заканчивая капиллярами, образуют сплошную среду. Многократно разветвляясь и делясь, они становятся столь узкими, что площадь их поперечного сечения оказывается сравнимой с размерами кровяной клетки.
В тканях пищеварительного тракта одна волнистая поверхность встроена в другую. Легкие также представляют собой пример того, как большая площадь «втиснута» в довольно маленькое пространство. В среднем площадь дыхательной поверхности легких человека больше площади теннисного корта. Но еще удивительнее то, как искусно пронизаны лабиринты дыхательных путей артериями и венами. Традиционное описание раз-ветвлений в бронхах оказалось в корне неверным; фрактальное же их изображение вполне подходит под практические данные.
Физическое тело человека фрактально; это уже признано и доказано. Принцип единого простого, задающего разнообразное сложное, заложен и в геноме человека, когда одна клетка живого организма содержит информацию обо всем организме в целом.
Рассматривая человека как многоуровневую информационную систему, как часть глобальной фрактальной конструкции Вселенной, ученые всецело зависят друг от друга, так как каждый объект генерирует определенные информационные сигналы – связи, влияющие на его окружение.
Любое воздействие на поверхность тела вызывает соответствующие реакции организма. На какой бы участок организма ни направить жесткую нагрузку, появляется болевое ощущение; следовательно, импульс раздражает соответствующий рецептор периферической нервной системы, имеющей фрактальную структуру. В свою очередь, отсутствие каких-либо сигналов говорит о наличии конкретной патологии.
Слайд 9 Если физические функции организма правильно взаимодействуют друг с другом, значит, существует
Если физические функции организма правильно взаимодействуют друг с другом, значит, существует

Истинное здоровье – это не отсутствие внешних проявлений болезни, а состояние внутренней гармонии, когда структура организма бесконфликтна и функционирует в оптимальном режиме. Организм развивается по базовой программе, и если эта функциональная основа искажена, то изменить его состояние возможно только при одном условии: нужно воздействовать на весь организм целиком, выравнивая его структурную форму и восстанавливая базовую матрицу функциональных процессов жизнедеятельности. В противном случае деформированная схема воздействий приведет к тому, что вновь и вновь информационные сбои будут проявляться как нарушение гармонии, как болезнь.
Но ведь нарушение гармонии происходит сначала на энергетическом уровне и только потом проявляется в физическом теле в виде каких-либо симптомов. Симптом является сигналом, нарушающим устоявшееся течение жизни, заставляющим обратить внимание на то, что у человека нарушен баланс внутренних душевных сил. При этом бессмысленно лечить какой-либо больной орган, конкретно «болезнь», нужно лечить весь организм в целом, интегративно.
Таким лечением или восстановлением структурных взаимосвязей организма, которые по какой-то причине были потеряны или извращены, занимается энергоинформационная медицина, уверенно набирающая силу.
Слайд 10Заключение
Хаос не нов, он существовал повсюду еще до появления времени
Заключение
Хаос не нов, он существовал повсюду еще до появления времени

Новейшие научные достижения – теория Хаоса и фрактальность мироздания – объясняют и доказывают взаимосвязь человека и Космоса, человека и его информационной составляющей, которая является фракталом информационного поля Вселенной. Со всей очевидностью становится ясно, что человек в самой основе – это духовная сущность. Именно эта сущность определяет нашу жизнь на Земле и наше здоровье.
Б. Мандельброт только систематизировал все знания о фракталах полученных ранее и преобразил их. Он описал их свойства, структуры фракталов. И эти сведения не остались не замеченными людьми. Основываясь на знаниях о фракталах они нашли им хорошее применение в повседневной жизни, например, создаются матрицы на основе фракталов, и эти матрицы используют в медицине для лечения органов и систем органов. Опираясь на структуру фрактальных объектов возводят сооружения, например, Эйфелева башня.
Слайд 11Универсальная методика
На сегодняшний день абсолютно ясно, что необходима принципиально новая методика
Универсальная методика
На сегодняшний день абсолютно ясно, что необходима принципиально новая методика

Аппликатор «AIRES®» прошел множественные испытания в различных институтах и клиниках Санкт-Петербурга.
Предлагаемая технология является принципиально новой методикой, основанной на понимании тонкостей информационно-обменных процессов биоформы, что, безусловно, можно назвать технологией XXI века, т.к. время тяжелых медикаментозных и энергоемких терапевтических воздействий безвозвратно уходит.
Аппликатор рекомендуется применять в комплексе традиционных мер при купировании умеренно выраженного болевого синдрома различного генеза (невралгии, миалгии, артралгии и пр.), лечение отека тканей и воспалительных реакций, а также с целью активации регенеративных процессов у пациентов с ранами мягких тканей и поверхностными ожогами.
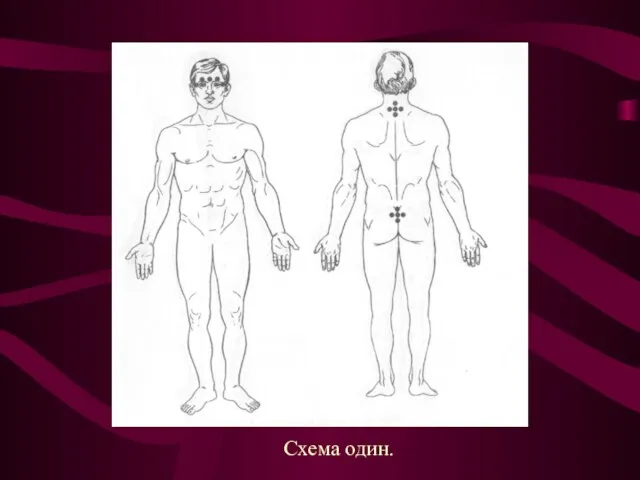
При фиксации аппликаторов необходимо соблюдать вертикально-ориентированное расположение осей аппликатора, а также симметричное расположение аппликаторов относительно вертикальной оси тела. Ширина стороны большого квадрата у каждого человека индивидуальна и равна расстоянию между его зрачками. Допустимая погрешность – 1 см.
Слайд 12 Воздействие аппликаторами осуществляется до появления оздоровительного эффекта. Время экспозиции аппликаторов может
Воздействие аппликаторами осуществляется до появления оздоровительного эффекта. Время экспозиции аппликаторов может

Слайд 13Схема один.
Схема один.
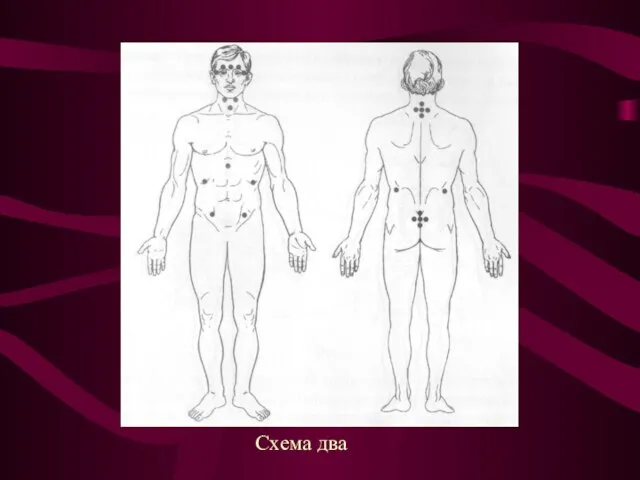
Слайд 14Схема два
Схема два
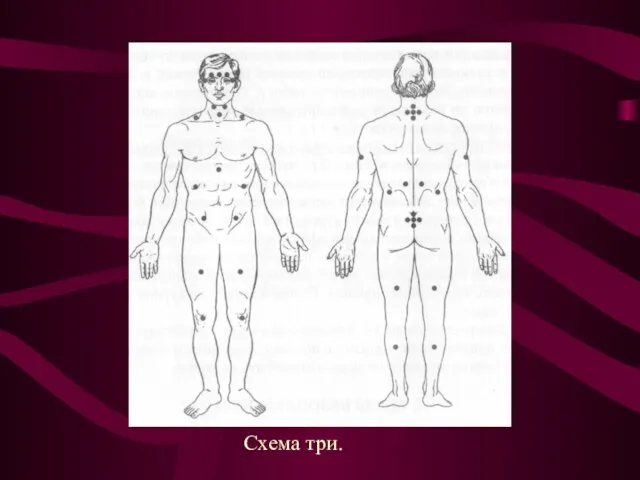
Слайд 15Схема три.
Схема три.
 Предквантум
Предквантум Старинные зимние обычаи и праздники, «Рождество», «Святки»
Старинные зимние обычаи и праздники, «Рождество», «Святки» ВИДЕО-СТЕНА DIBOSS LB-40
ВИДЕО-СТЕНА DIBOSS LB-40 Новый подход к интеграции календарно-сетевых графиков и смет
Новый подход к интеграции календарно-сетевых графиков и смет Областной конкурс Методическая разработка дистанционного урока - 2021
Областной конкурс Методическая разработка дистанционного урока - 2021 Музей путешествий. Поклонная гора. Парк Победы
Музей путешествий. Поклонная гора. Парк Победы Товары и услуги
Товары и услуги Техническое регулирование
Техническое регулирование 20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona
20140305_lekarstvennye_rasteniya_buturlinovskogo_rayona Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4.
Консолидация ритейла в Украине: роль логистики 1.Предпосылки для консолидации ритейла 2.Когда ритейлеру нужен 3PL-оператор? 3.Case study 4. Project on the Indian Ocean
Project on the Indian Ocean  Портретная студийная съёмка
Портретная студийная съёмка Внешняя политика Советского государства 1920-х
Внешняя политика Советского государства 1920-х СТРОКА, ОБОРВАННАЯ ПУЛЕЙ
СТРОКА, ОБОРВАННАЯ ПУЛЕЙ ЕГЭ В 3 «Площади»
ЕГЭ В 3 «Площади» Цветовой контраст (хроматический)
Цветовой контраст (хроматический) Фотожурналист Владимир Вяткин
Фотожурналист Владимир Вяткин 26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе
26-27 апреля 2006 года Центр практической психологии РГУ имени С.А. Есенина Московский городской психолого-педагогический университе Кейс-стади для педагогов
Кейс-стади для педагогов Об аксиомах геометрии
Об аксиомах геометрии Презентация на тему Родная природа в стихотворениях поэтов xx века
Презентация на тему Родная природа в стихотворениях поэтов xx века  Каталог Атоми
Каталог Атоми Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе
Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по русскому языку Соловьева Т.В., предсе Создание новогодней открытки на основе пейзажа «Зимние россыпи»
Создание новогодней открытки на основе пейзажа «Зимние россыпи» Внесем порядок в хаос! ИЗО 7 класс
Внесем порядок в хаос! ИЗО 7 класс Космонавты, рожденные Украиной: космонавты Луганщины
Космонавты, рожденные Украиной: космонавты Луганщины Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства»
Межрегиональный образовательный форум «Открытое образовательное пространство: живая праКтика тьюторства» ДДК. Экскурсия
ДДК. Экскурсия