Funcţii

Utilizatori Conturi în sistem de e-mail
(”nume utilizator”1 şi parolă1) →
[email protected]
(”nume utilizator”2 şi parolă2) →
[email protected]
(”nume utilizator”3 şi parolă3) → ∅
CORESPONDENŢE (SAU LEGI DE CORESPONDENŢĂ)

O funcţie este determinată de trei elementeaaa X , Y şi f, având următoarele semnificaţii: X și Y sunt mulțimi, iar f este o lege de corespondență de la X la Y care face ca:
fiecărui element x ∈ X să-i corespundă un element și numai unul y ∈ Y. (2.1)
Astfel o funcţie este un triplet (X, Y, f). Acest triplet se notează în mod frecvent prin f: X → Y. Elementele constitutive ale funcţiei se numesc:
X – domeniu (sau domeniu de definiție);
Y – codomeniu (sau domeniu de valori);
f – lege de corespondenţă..
DEFINIŢIA FUNCŢIEI

Fie f: X → Y și f(x) = y ∈ Y unde x ∈ X, atunci:
y se numește imaginea lui x prin f;
x se numește preimaginea (sau imaginea inversă) lui y prin f.
Este posibiliă notația f−1(y) = x.
Fie corespondența:
Șiruri: “q”, “qw”, “qwerty”,
“qwertz”;
Lungimea: 1, 2, 6.
Dacă notăm funcția prin L atunci:
L−1(1) = q; L−1(6) = {qwerty,
qwertz};
IMAGINE ȘI PREIMAGINE

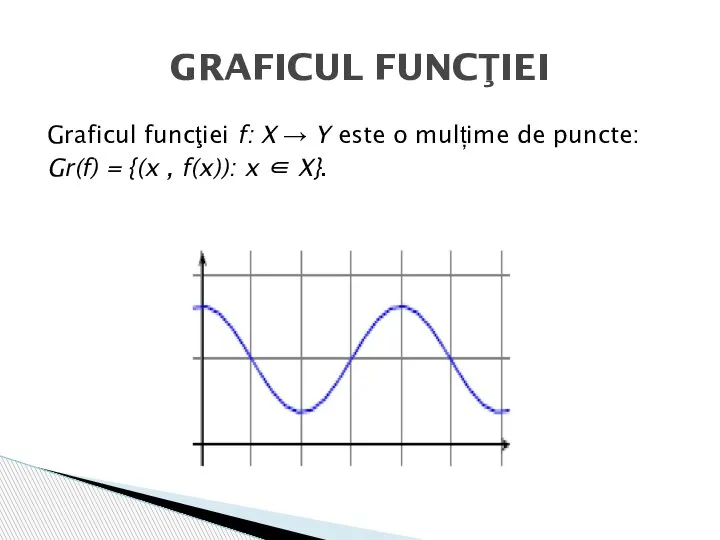
Graficul funcţiei f: X → Y este o mulțime de puncte:
Gr(f) = {(x , f(x)): x ∈ X}.
GRAFICUL FUNCŢIEI

Nu orice grafic este grafic de funcţie.
Condiţia (2.1) este formată din două subcondiții:
fiecărui element x din domeniu îi corespunde un element în codomeniu, adică
∀x ∈ X , ∃y ∈ Y încît y = f(x). (2.2)
elementul din codomeniu ce corespunde unui x este unic, adică
∀x1, x2 ∈ X, x1 = x2 ⇒ f(x1) = f(x2). (2.3)
GRAFICUL FUNCŢIEI

Cu ajutorul paralelelor la axele de coordonate recunoaştem îndeplinirea condițiilor (2.2) și (2.3) astfel:
Un grafic satisface condiţia (2.2) dacă și numai dacă orice paralelă la axa ordonatelor dusă prin punctele domeniului întâlnește graficul în cel puțin un punct;
Un grafic satisface condiţia (2.3) dacă și numai dacă orice paralelă la axa ordonatelor dusă prin punctele domeniului întâlnește graficul în cel mult un punct.
GRAFICUL FUNCŢIEI

Periodice – funcţiile trigonometrice;
Pare;
Monotone;
Injective;
Surjective;
Bijective.
PROPRIETĂȚI ALE FUNCȚIILOR

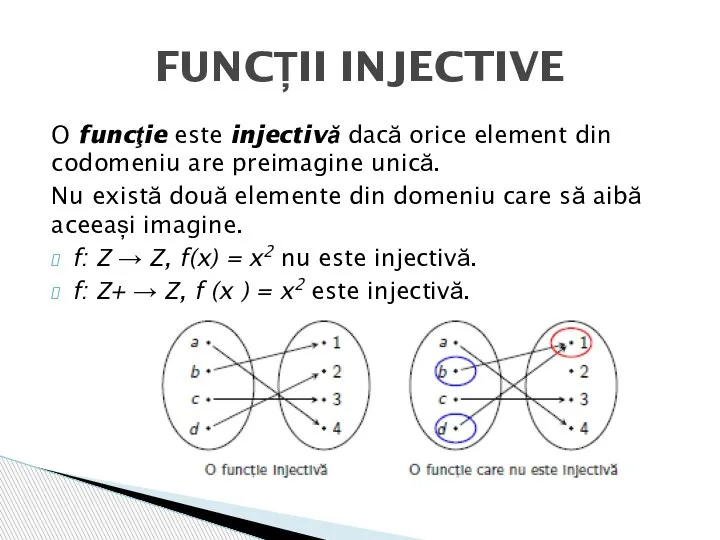
O funcţie este injectivă dacă orice element din codomeniu are preimagine unică.
Nu există două elemente din domeniu care să aibă aceeași imagine.
f: Z → Z, f(x) = x2 nu este injectivă.
f: Z+ → Z, f (x ) = x2 este injectivă.
FUNCȚII INJECTIVE

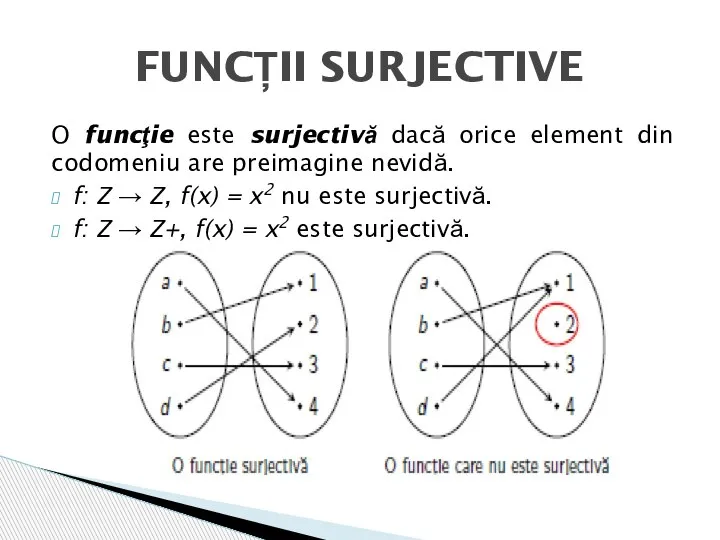
O funcţie este surjectivă dacă orice element din codomeniu are preimagine nevidă.
f: Z → Z, f(x) = x2 nu este surjectivă.
f: Z → Z+, f(x) = x2 este surjectivă.
FUNCȚII SURJECTIVE

O funcţie bijectivă = injectivă și surjectivă.
FUNCȚII BIJECTIVE

Cu ajutorul paralelelor la axele de coordonate recunoaștem dacă un grafic este graficul unei funcții injective sau surjective, astfel:
Un grafic este graficul unei funcţii injective dacă și numai dacă orice paralelă la axa absciselor dusă prin punctele codomeniului întâlnește graficul în cel mult un punct;
Un grafic este graficul unei funcţii surjective dacă și numai dacă orice paralelă la axa absciselor dusă prin punctele codomeniului întâlnește graficul în cel puțin un punct.
RECUNOAȘTEREA FUNCȚIILOR INJECTIVE, SURJECTIVE

Funcția compusă (g◦f)(x) = g(f(x)).
Operaţia se numește: compunerea funcțiilor (operații în lanț).
Fie f(x) = 2x2 − 3x + 1 și g(x) = 3x + 1 atunci f ◦ g = f(g(x)) = 2(3x + 1)2 − 3(3x + 1) + 1.
OPERAŢII CU FUNCȚII: COMPUNEREA FUNCȚIILOR

Fie f: X → Y, g: X → Y.
Adunarea f + g = f(x) + g(x).
Înmulţirea f · g = f(x) · g(x).
Inversând legea de corespondență (inversând sensul săgeților) pentru o funcție oarecare f: X → Y nu se obține totdeauna o funcție.
Pentru ca inversând legea de corespondență să fie satisfăcută condiția (2.3) este necesar și suficient ca prin funcția directă puncte diferite să aiba imagini diferite, adică:
∀x1, x2 ∈ X, x1 ≠ x2 ⇒ f(x1) ≠ f(x2).
Pentru ca inversând legea de corespondență să fie satisfăcută condiția (2.2) este necesar și suficient ca prin funcția directă să se consume toate punctele din codomeniu, adică:
∀y ∈ Y, ∃x ∈ X: f(x) = y.
OPERAŢII CU FUNCȚII: OPERAȚII ALGEBRICE, INVERSA UNEI FUNCȚII

Un actuar și un agricultor călătoresc cu trenul. Când au trecut pe lângă o pajiște pe care se afla o turmă de oi, actuarul a spus, ”Nu există 1248 de oi acolo”. Agricultorul a răspuns, ”Extraordinar. Din întâmplare, eu îl cunosc pe proprietarul oilor, iar cifra este absolut corectă. Cum de le-ai numărat atât de repede?”. Actuarul a răspuns, ”Foarte simplu, am numărat doar numărul de picioare și am împărțit la patru”.
Cu ajutorul funcţiilor bijective putem numără elementele unei mulţimi numărând altă mulțime.
Dacă f: X → Y este o bijecție atunci numărând elementele mulţimii X de fapt numărăm și elementele mulțimii Y; şi invers.
NUMĂRAREA CU AJUTORUL FUNCȚIILOR (CARDINAL)

Două mulțimi se numesc echivalente dacă putem găsi o funcție bijectivă definită pe una din mulțimi și cu valori în cealaltă mulțime.
Principiul cutiilor lui Dirichlet:
O funcție f: X → Y unde X și Y sunt mulțimi finite cu |X|> |Y| nu poate fi injectivă; trebuie să existe cel puțin două elemente din X care să aibă aceeași imagine în Y.
1. Dacă într-un auditoriu sunt 367 de oameni atunci, cel puțin 2 din ei s-au născut în aceeași zi (pentru că avem mai mulți oameni decât zile în an).
2. Într-o pădure de conifere creșteau 800 000 de brazi, astfel încât nici unul din ei nu avea mai mult de 500 000 de ace; să se demonstreze că cel puțin doi brazi posedă același număr de ace.
FUNCȚII DE ECHIVALENȚE. PRINCIPIUL LUI DIRICHLET