Содержание
- 2. На прошлой лекции… На прошлой лекции научились работать со структурами «с нулевой площадью» на изображении (с
- 3. Что такое сегментация? Анализ высокого уровня: отделение находящихся на изображении объектов от фона (и друг от
- 4. Автоматика и интерактивность Подразделяем Автоматическая Сегментация производимая без взаимодействия с пользователем Картинка на входе, регионы на
- 5. Применение сегментации Фото(видео)монтаж, композиция
- 6. Применение сегментации Измерение параметров объектов
- 7. Применение сегментации Предобработка перед высокоуровневым анализом
- 8. Определение сегментации 1 «Жесткая» сегментация Разбиение изображения на неперекрывающиеся области, покрывающие все изображение и однородные по
- 9. Рассмотрим семейства методов: Основанные на поиске краев Основанные на формировании однородных областей Метод водораздела / tobogganing
- 10. Автоматическая сегментация Как можно сформировать однородные области? Отталкиваясь от неоднородности на границах Пример – ищем резкие
- 11. Однородность Варианты однородности: По яркости По цвету По близости на изображении По текстуре По глубине (Если
- 12. Сегментация через поиск неоднородностей Наиболее простой и чаще всего используемый вариант: Поиск неоднородностей яркости через выделение
- 13. Алгоритм Найдём все контура на изображении алгоритмом Canny; Найдем все замкнутые контура; «Внутренности» замкнутых контуров являются
- 14. Сегментация через поиск однородных областей План Сегментация без учета пространственных связей Пороговая фильтрация Кластеризация по цвету
- 15. Пороговая фильтрация Разделение пикселей на n классов по их яркости Чаще всего используется 2 класса (бинаризация)
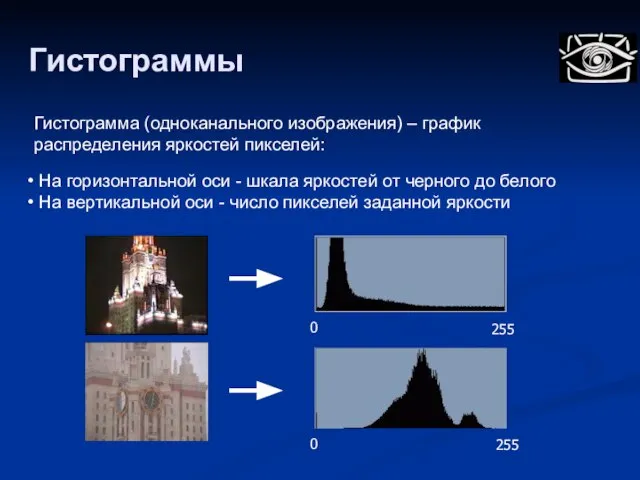
- 16. Гистограммы Гистограмма (одноканального изображения) – график распределения яркостей пикселей: На горизонтальной оси - шкала яркостей от
- 17. Гистограммы Свойства: Рассчитываются глобально для всего изображения Пространственная информация (расположение пикселей различной яркости) полностью игнорируется Это
- 18. Гистограммы Свойства: Рассчитываются глобально для всего изображения Пространственная информация (расположение пикселей различной яркости) полностью игнорируется Это
- 19. Гистограммы Свойства: Рассчитываются глобально для всего изображения Пространственная информация (расположение пикселей различной яркости) полностью игнорируется Однако
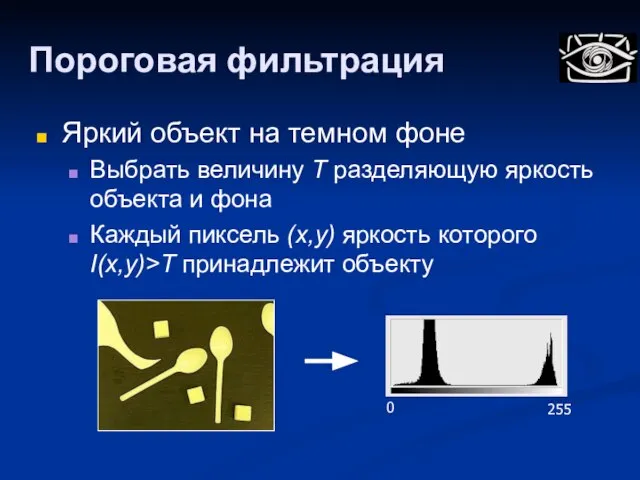
- 20. Пороговая фильтрация Яркий объект на темном фоне Выбрать величину T разделяющую яркость объекта и фона Каждый
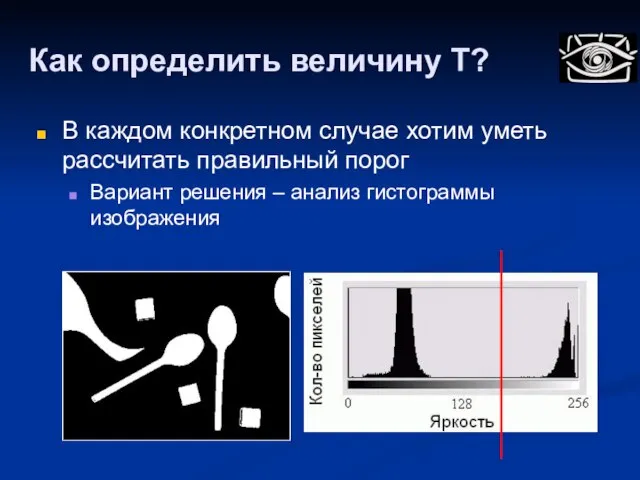
- 21. Как определить величину T? В каждом конкретном случае хотим уметь рассчитать правильный порог Вариант решения –
- 22. Автоопределение величины T Можно использовать следующее: 1. Предположение о яркости объектов 2. Размеры объектов 3. Площадь
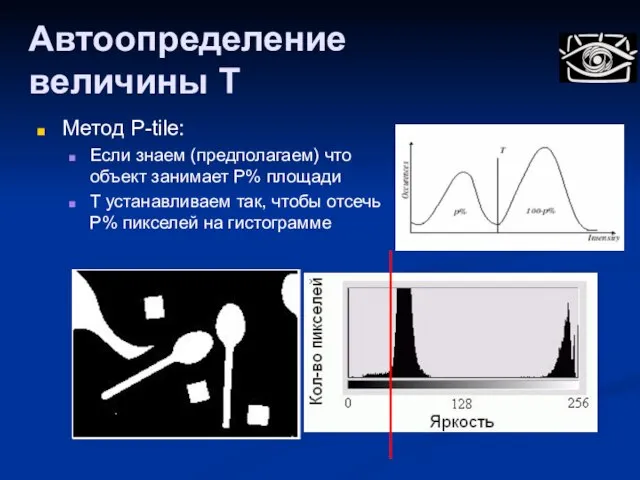
- 23. Автоопределение величины T Метод P-tile: Если знаем (предполагаем) что объект занимает P% площади T устанавливаем так,
- 24. Расчет T путем последовательных приближений Частный случай алгоритма k-средних Выбрать порог T равным середине диапазона яркостей;
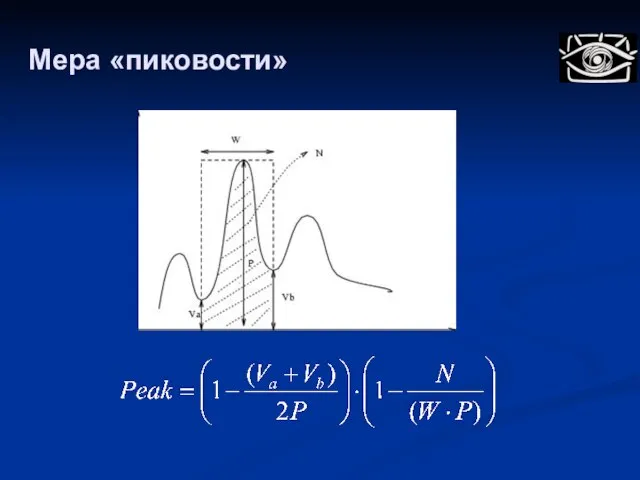
- 25. Поиск пиков в гистограмме Найти соседние локальные максимумы в гистограмме gi Рассчитать меру «пиковости» для gi
- 26. Мера «пиковости»
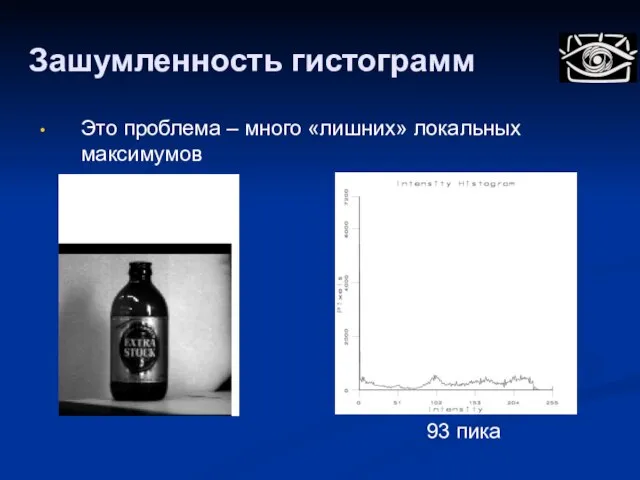
- 27. Зашумленность гистограмм 93 пика Это проблема – много «лишних» локальных максимумов
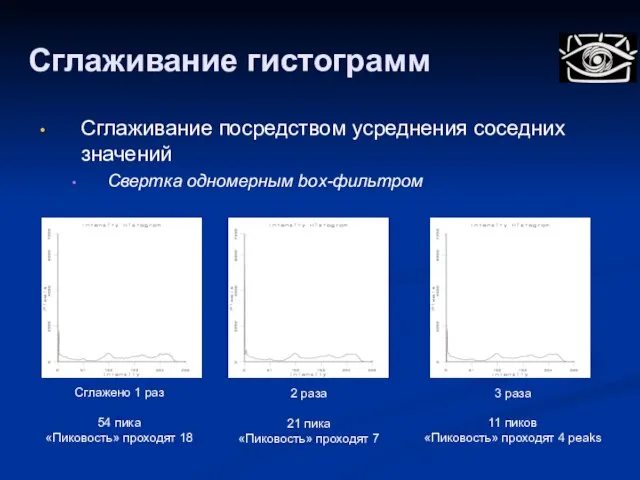
- 28. Сглаживание гистограмм Сглажено 1 раз 54 пика «Пиковость» проходят 18 2 раза 21 пика «Пиковость» проходят
- 29. Области найденные по пикам
- 30. Адаптивный порог Проблема: Яркость фона может быть разной в разных частях изображения Единый порог не подойдет
- 31. Адаптивный порог Для каждого пикселя изображения I(x, y): В окрестности пикселя радиуса r высчитывается индивидуальная для
- 32. Адаптивный порог r=7, T=0 r=7, T=7 r=75, T=10 Исходное
- 33. Адаптивный порог Другая формулировка Приближение фона усреднением Вычитание фона - I(x, y) – C(x,y) > T
- 34. Адаптивный порог Хорошо работает Когда размер искомого объекта заметно меньше размера оцениваемой окрестности Хуже работает, Когда
- 35. Кластеризация k-средних Способ определения нескольких порогов одновременно Нужно заранее знать k - количество диапазонов яркостей В
- 36. Алгоритм k-средних Случайным образом выбрать k средних mj j=1,…,k; Для каждого vi i=1,…,p подсчитать расстояние до
- 37. Пример кластеризации в 2D Исходные данные
- 38. Пример кластеризации в 2D Случайная инициализация центров кластеров (шаг 1)
- 39. Пример кластеризации в 2D Кластеры после первой итерации (шаг 2)
- 40. Пример кластеризации в 2D Пересчет центров кластеров после первой итерации (шаг 3)
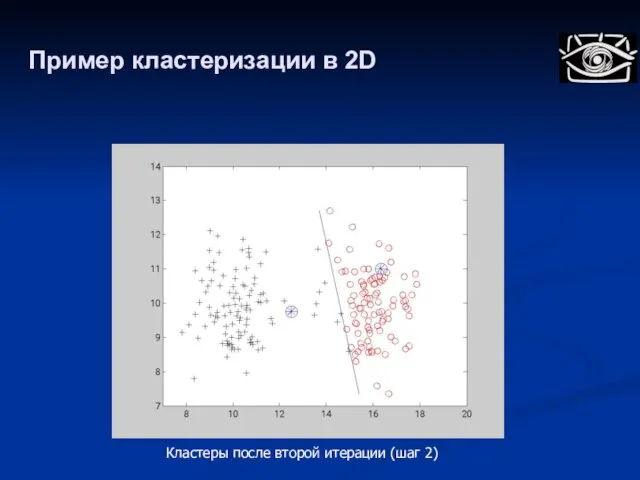
- 41. Пример кластеризации в 2D Кластеры после второй итерации (шаг 2)
- 42. Пример кластеризации в 2D Стабильная конфигурация после четвертой итерации
- 43. k-средних для сегментации Если изображение одноканальное vi = I(x, y) – работаем в одномерном пространстве Получается
- 44. Алгоритм k-средних для одноканального изображения Случайным образом выбрать k средних mj j=1,…,k; Для каждого пикселя (x,y)
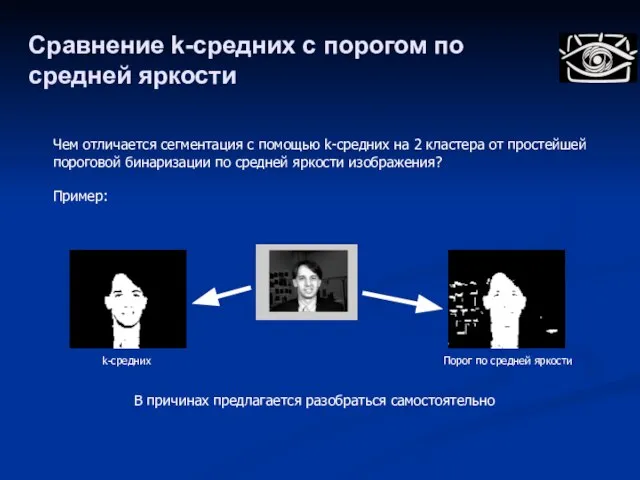
- 45. Сравнение k-средних с порогом по средней яркости Чем отличается сегментация с помощью k-средних на 2 кластера
- 46. Общие недостатки описанного Игнорируется пространственное расположение пикселей За исключением адаптивного порога, но и там соседство не
- 47. Понятие связности Определение связной области: Множество пикселей, у каждого пикселя которого есть хотя бы один сосед,
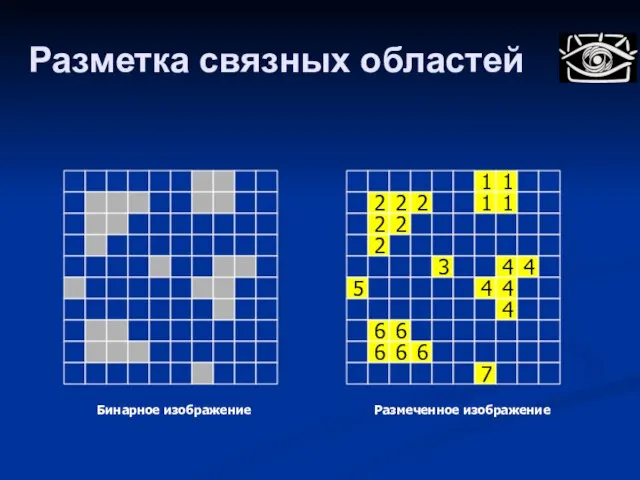
- 48. Разметка связных областей 1 1 2 2 2 1 1 2 2 2 3 4 4
- 49. Разрастание регионов (Region growing) Простая идея – начиная с некоторого “семени” обходить пиксели и объединять в
- 50. Что необходимо определить Критерий однородности Гистограмма содержит не больше 1 значительного пика Отклонение любого пикселя от
- 51. Пример δ = 1 Алгоритм разрастания регионов Среднее: 1 Среднее: 1.125
- 52. Алгоритм разрастания регионов Пример δ = 1
- 53. Разрастание регионов if |I(A) – Clavg(B)| > δ and |I(A) – Clavg(C)| > δ - создаем
- 54. Разделение областей Первый шаг – всё изображение это одна область, поместить область в стек Пока стек
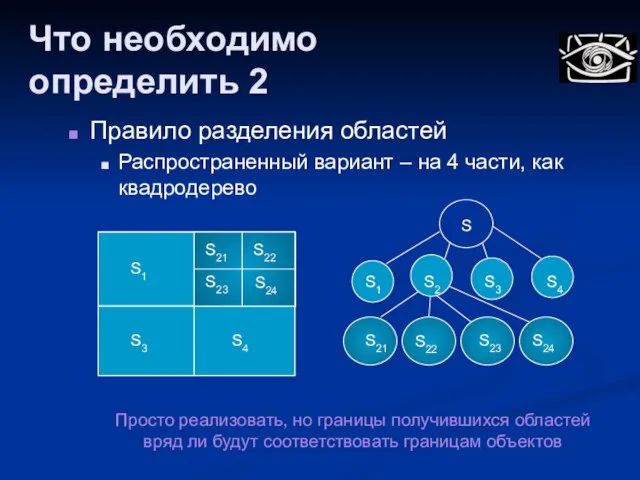
- 55. Что необходимо определить 2 Правило разделения областей Распространенный вариант – на 4 части, как квадродерево Просто
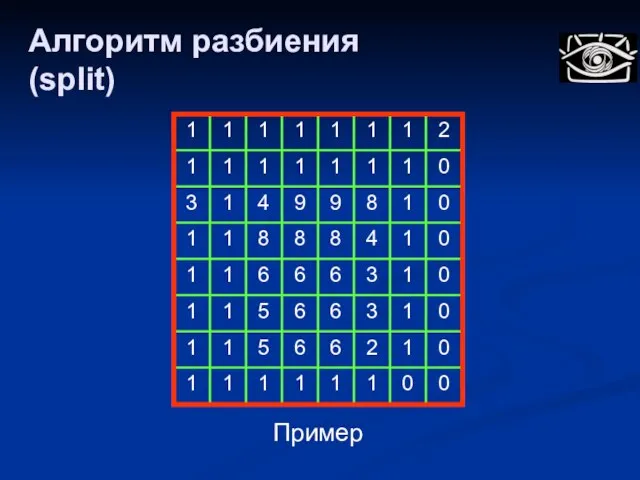
- 56. Пример Алгоритм разбиения (split)
- 57. Первое разбиение Алгоритм разбиения (split)
- 58. Второе разбиение Алгоритм разбиения (split)
- 59. Третье разбиение Алгоритм разбиения (split)
- 60. Что необходимо определить 3 Правило разделения областей – более умно Найти в гистограмме пики, разделить гистограмму
- 61. Слияние областей Первый шаг – каждый пиксель это отдельная область, поместить все области в стек Пока
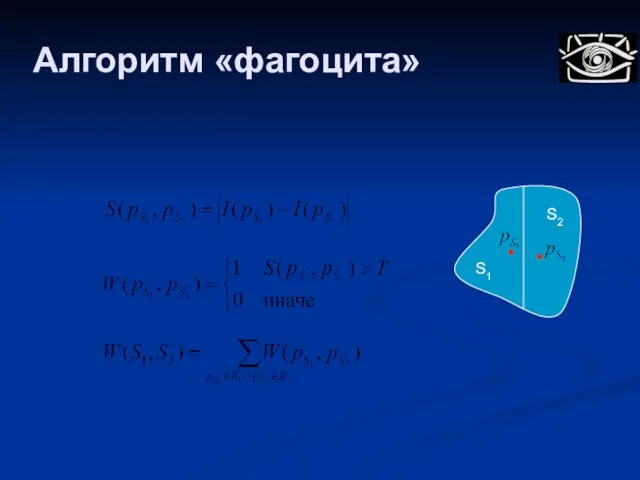
- 62. Алгоритм «фагоцита» Истаивание границ Убирает слабые границы «Слабость границ» определяется по разности яркостей граничных пикселей S1
- 63. Алгоритм «фагоцита» S1 S2
- 64. Алгоритм «фагоцита» Слить две области если: где P1 и P2 – периметры областей S1 and S2
- 65. Алгоритмы разбиения и слияния Недостатки: Разбиение Может дать слишком много регионов Если использовать квадродерево, границы скорее
- 66. Алгоритм разбиения/слияния (split and merge) Идея: Сначала провести разбиение на небольшие однородные области Обычно используется принцип
- 67. Слияние Алгоритм разбиения/слияния (split and merge)
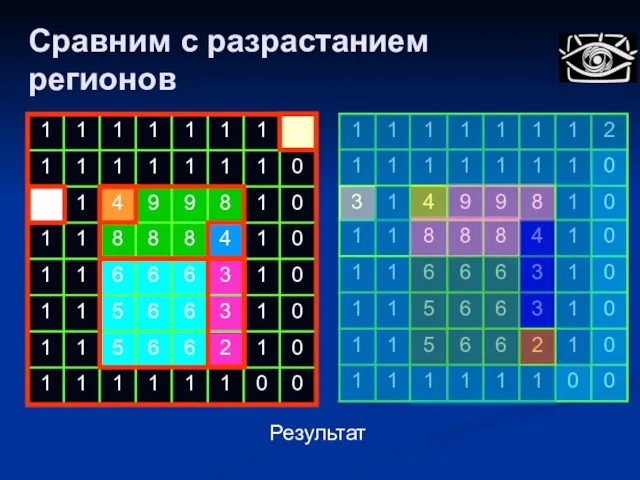
- 68. Результат Алгоритм разбиения/слияния (split and merge)
- 69. Результат Сравним с разрастанием регионов
- 70. Сравним подходы Сегментация на основе областей В результате всегда замкнутые границы областей Использование многоканальных изображений (RGB,
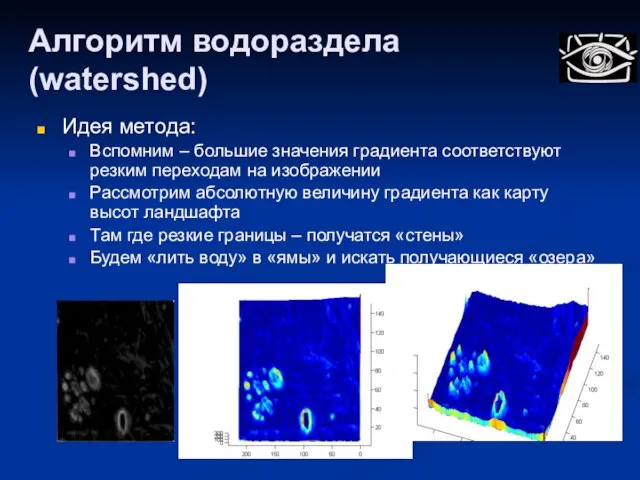
- 71. Алгоритм водораздела (watershed) Идея метода: Вспомним – большие значения градиента соответствуют резким переходам на изображении Рассмотрим
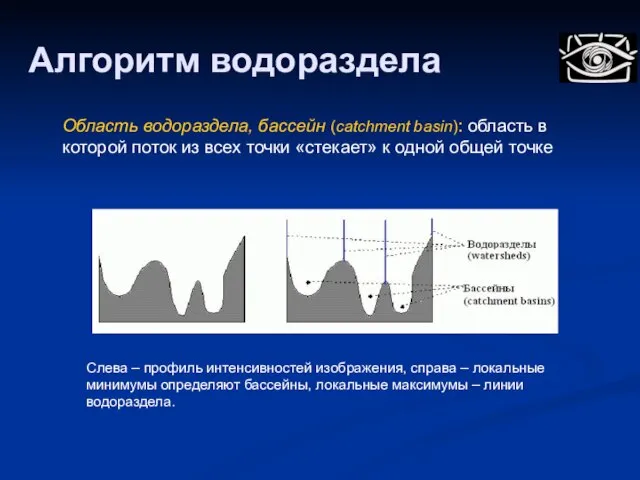
- 72. Алгоритм водораздела Область водораздела, бассейн (catchment basin): область в которой поток из всех точки «стекает» к
- 73. Алгоритм водораздела Алгоритм, как и разбиение дает множество небольших регионов Очень чувствителен к шуму – ищет
- 74. Алгоритм «погружения» Алгоритм «погружения» (immersion) : Начнем с самых «глубоких» (темных) пикселей (они определят начальные бассейны)
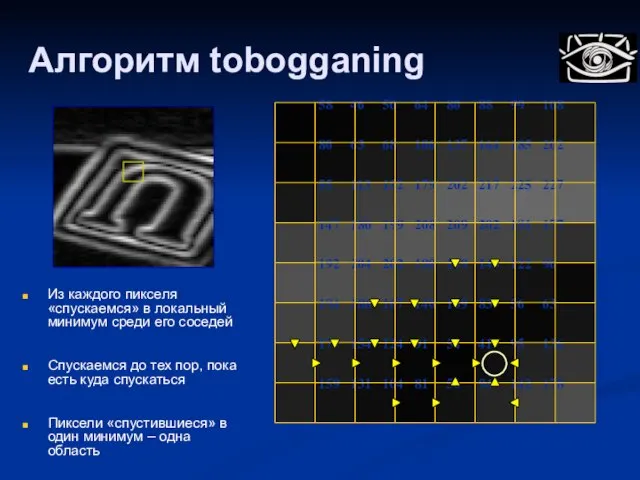
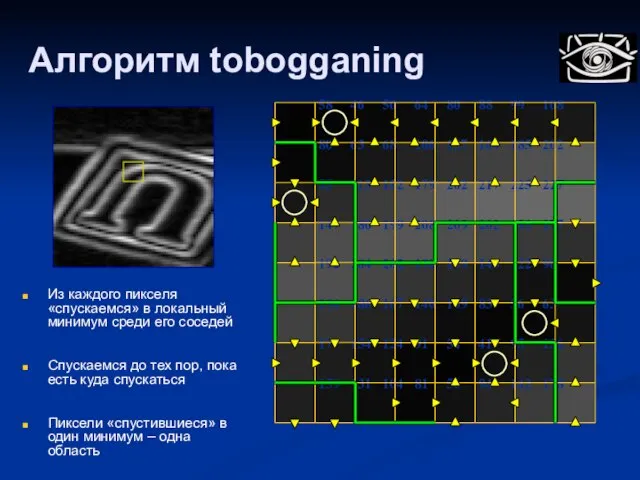
- 75. Алгоритм tobogganing Идея: Из каждого пикселя «спускаемся» в локальный минимум среди его соседей Спускаемся до тех
- 76. Алгоритм tobogganing 58 46 50 64 80 88 99 108 80 63 68 106 137 164
- 77. Алгоритм tobogganing 58 46 50 64 80 88 99 108 80 63 68 106 137 164
- 78. Tobogganing и водораздел В зависимости от задачи можно анализировать само изображение абсолютную величину его градиента distance
- 79. Методы теории графов Теория графов – хороший инструмент для работы с изображениями Хорошая теоретическая база Много
- 80. Граф и изображение Изображение превращается во взвешенный неориентированный граф Пиксели – вершины графа Ребра – связи
- 81. Критерии «похожести» пикселей По расстоянию По яркости По цвету По текстуре
- 82. Создать граф Разрезать граф Каждую связную компоненту после разреза рассматривать как отдельную область Сегментация с помощью
- 83. Разрез графа G=(V,E) Непересекающиеся подмножества вершин A и B из V Удаляем все ребра, связывающие A
- 84. Разрез графа Разрез графа превращает граф в два несвязанных друг с другом подграфа
- 85. Разрез графа Если множества A и B не заданы заранее – разрезать граф можно по-разному: Минимальный
- 86. Минимальный разрез хорош не всегда На данном рисунке вес ребер графа показан расстоянием между вершинами
- 87. Нормализованный разрез графа (Normalized cut) Другая мера разреза – измеряет «похожесть» двух групп вершин, нормированную на
- 88. Минимальный нормализованный разрез Минимальный нормализованный разрез – разрез, превращающий граф в несвязный, с минимальной величиной NCut
- 89. Матрицы… D – диагональная матрица n x n: W is an n x n symmetrical matrix
- 90. Можно вывести что: При условиях: Если разрешить задача сводится к задаче на собственные значения:
- 91. Алгоритм сегментации c помощью normalized cuts Задать граф на изображении. Рассчитать матрицы W и D Решить
- 92. Пример:
- 93. Подытожим: Рассмотрели следующие методы Использующие края Edge-based Пороговой фильтрации Thresholding k-средних k-means Разрастания регионов Region growing
- 94. Анализ областей после сегментации Владимир Вежневец, Антон Конушин Александр Вежневец Курс – «Введение в компьютерное зрение»
- 95. Какие параметры формы областей помогут различить объекты на этом примере?
- 96. Свойства области Характеристики границы области См. предыдущую лекцию Площадь Кол-во «дырок» внутри Центр масс Периметр Компактность
- 97. Площадь Кол-во пикселей в области
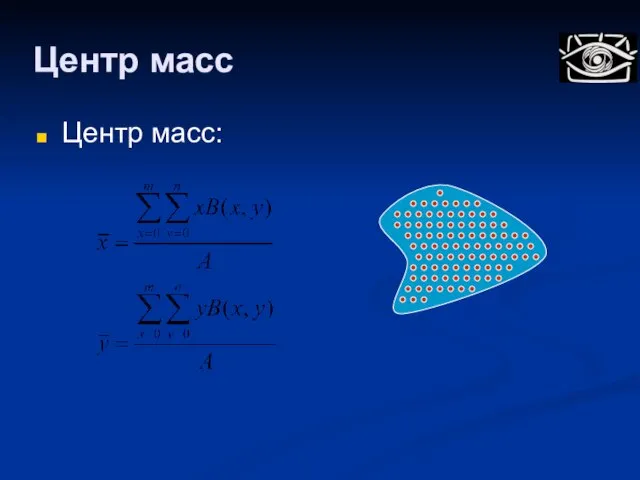
- 98. Центр масс Центр масс:
- 99. Периметр и компактность Периметр - количество пикселей принадлежащих границе области Компактность Наиболее компактная фигура – круг,
- 100. Подсчет периметра области Пиксель лежит на границе области, если он сам принадлежит области и хотя бы
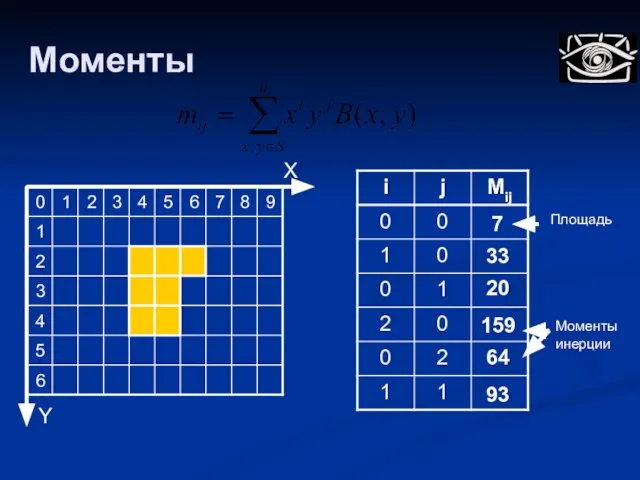
- 101. Дискретный момент mij области определяется следующим образом: - значение пикселя изображения Моменты
- 102. X Y 7 Площадь 20 33 159 Моменты инерции 64 93 Моменты
- 103. Центральные моменты Инвариантны к переносу Центр масс области
- 104. Центральные моменты
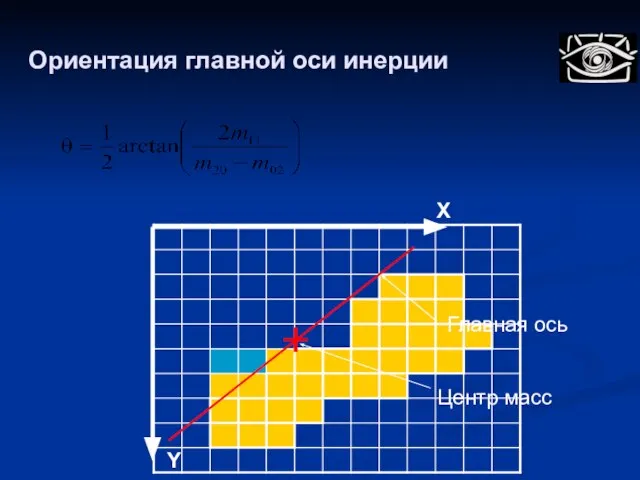
- 105. Ориентация главной оси инерции Главная ось Центр масс
- 106. Моменты Hu Инвариантны к повороту, переносу, скалированию
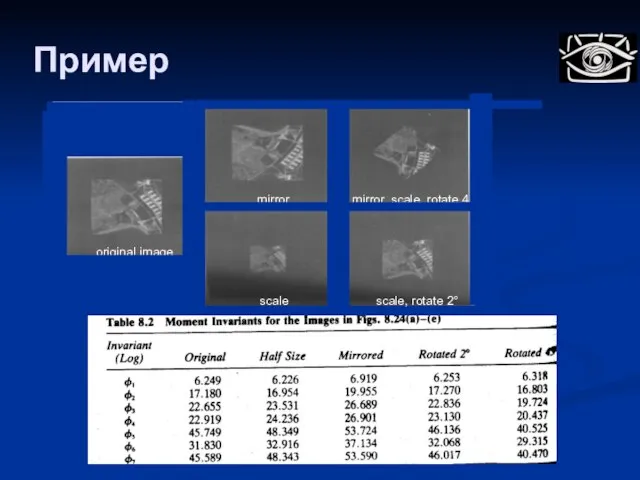
- 107. Пример
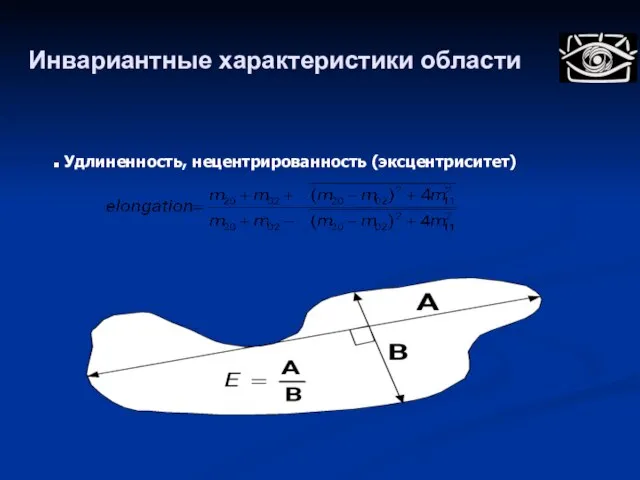
- 108. Инвариантные характеристики области Удлиненность, нецентрированность (эксцентриситет)
- 109. Цвет, яркость Цвет и яркость области тоже хорошие признаки. Варианты Гистограмма яркости, цветов в данной области
- 110. Немного о машинном обучении Мы рассмотрели сейчас методы «низкого уровня» Они анализируют небольшое кол-во «простой» информации
- 111. Задание Выдадим на следующей лекции Выполнятся будем на MATLAB Всем желающим получить задание нужно будет записаться
- 113. Скачать презентацию























































































 Госзакупки. С чего начать
Госзакупки. С чего начать Социальные деньги и платежи в социальных сетях.Способы монетизации игрового трафика и премиум сервисов.
Социальные деньги и платежи в социальных сетях.Способы монетизации игрового трафика и премиум сервисов. Всього одна чарка
Всього одна чарка ИЗУЧАЕМ EXCEL
ИЗУЧАЕМ EXCEL Институт кураторов — копия
Институт кураторов — копия Богатыри - герои былин
Богатыри - герои былин Острые респираторные заболевания и их профилактика
Острые респираторные заболевания и их профилактика Работа Эйвазова Фарида Школа-лицей 264,8d. Любое вещество может находиться в трёх агрегатных состояниях, таких как: Жидкое Твёрдое Га
Работа Эйвазова Фарида Школа-лицей 264,8d. Любое вещество может находиться в трёх агрегатных состояниях, таких как: Жидкое Твёрдое Га Геометрия в моде
Геометрия в моде Презентация на тему Аллея героев Первой мировой войны
Презентация на тему Аллея героев Первой мировой войны Публичный отчёт по основным направлениям развития 17.02.2011 Муниципальное автономное образовательное учреждение средняя общеобраз
Публичный отчёт по основным направлениям развития 17.02.2011 Муниципальное автономное образовательное учреждение средняя общеобраз CHOOSING A PROFESSION
CHOOSING A PROFESSION внутреннее строение насекомых
внутреннее строение насекомых 984967 (3)
984967 (3) Условие не превышения границы области допустимых состояний конструкции
Условие не превышения границы области допустимых состояний конструкции Положение об общественном совете муниципального образования
Положение об общественном совете муниципального образования Традиции модернизма в искусстве 2-й пол. ХХ века
Традиции модернизма в искусстве 2-й пол. ХХ века Лакомства для домашних питомцев из рога и субпродуктов ТМ Живкус
Лакомства для домашних питомцев из рога и субпродуктов ТМ Живкус Полные квадратные уравнения
Полные квадратные уравнения Конституция Республики Молдова
Конституция Республики Молдова Методическая работа школы
Методическая работа школы Набор в секции. Отделение сложно-координационных видов
Набор в секции. Отделение сложно-координационных видов Виктор Федорович Боков
Виктор Федорович Боков Chapter-8. Learning goals
Chapter-8. Learning goals Методи цитологічних досліджень
Методи цитологічних досліджень Реальная государственная поддержка сельского хозяйства! Миссия Корпорации – участие в реализации государственной политики агра
Реальная государственная поддержка сельского хозяйства! Миссия Корпорации – участие в реализации государственной политики агра Использование XSLT для разработки сайтов (на ASP.NET) Андрей Майоров, BYTE-force
Использование XSLT для разработки сайтов (на ASP.NET) Андрей Майоров, BYTE-force