Содержание
- 2. Геометрическое исследование решений ограниченной задачи трех тел Прикладные аспекты Излагается геометрическая интерпретация решения ограниченной проблемы трех
- 3. М. Л. Лидов. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел. Искусственные Спутники
- 4. Интегралы пространственной двукратно-осредненной ограниченной круговой задачи трех тел, полученные М. Л. Лидовым a = const; c1
- 5. Системы координат, используемые для геометрических исследований полярный радиус - наклонение i (0 полярный угол - аргумент
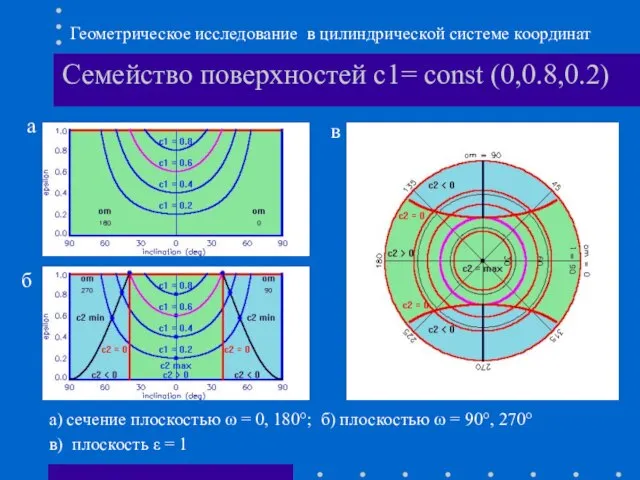
- 6. Семейство поверхностей c1= const (0,0.8,0.2) а) сечение плоскостью ω = 0, 180°; б) плоскостью ω =
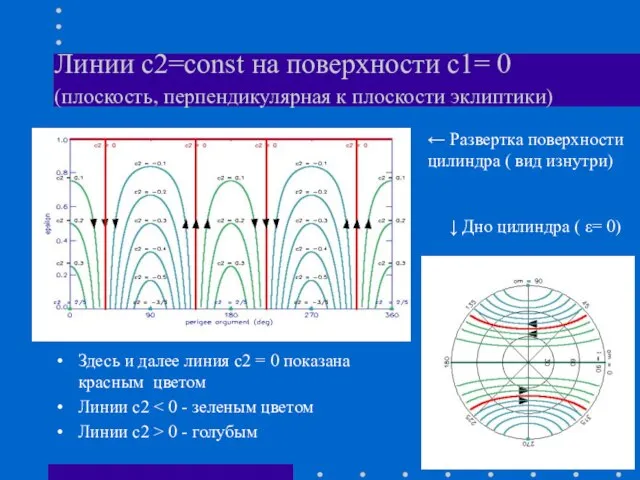
- 7. Линии с2=const на поверхности с1= 0 (плоскость, перпендикулярная к плоскости эклиптики) Здесь и далее линия с2
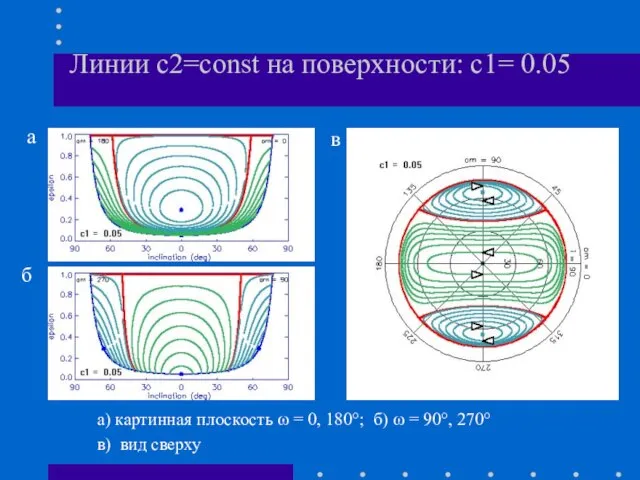
- 8. Линии с2=const на поверхности: с1= 0.05 а) картинная плоскость ω = 0, 180°; б) ω =
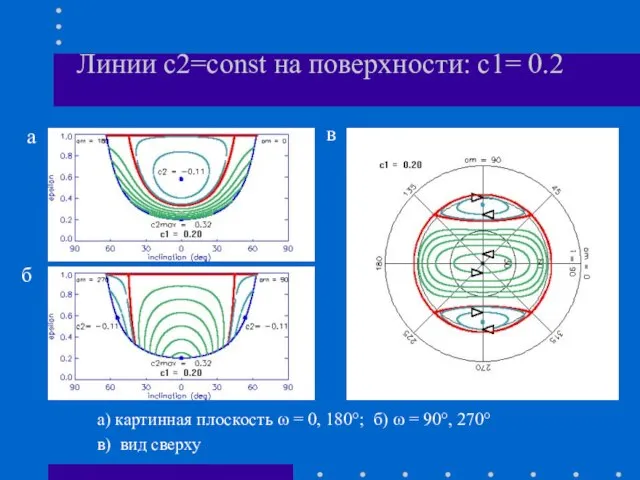
- 9. Линии с2=const на поверхности: с1= 0.2 а) картинная плоскость ω = 0, 180°; б) ω =
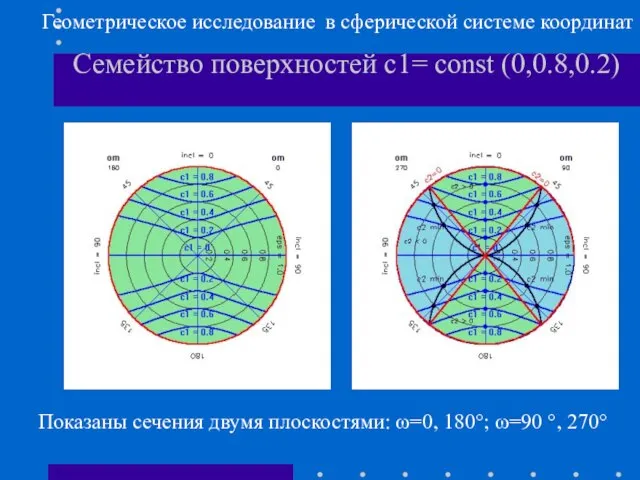
- 10. Семейство поверхностей c1= const (0,0.8,0.2) Показаны сечения двумя плоскостями: ω=0, 180°; ω=90 °, 270° Геометрическое исследование
- 11. Линии с2=const на поверхности с1= 0 (плоскость, перпендикулярная к плоскости эклиптики) Здесь и далее линия с2
- 12. Линии с2=const на поверхностях c1= const (при с1 = 0.05, 0.4, 0.6, 0.8) Картинные плоскости: а)
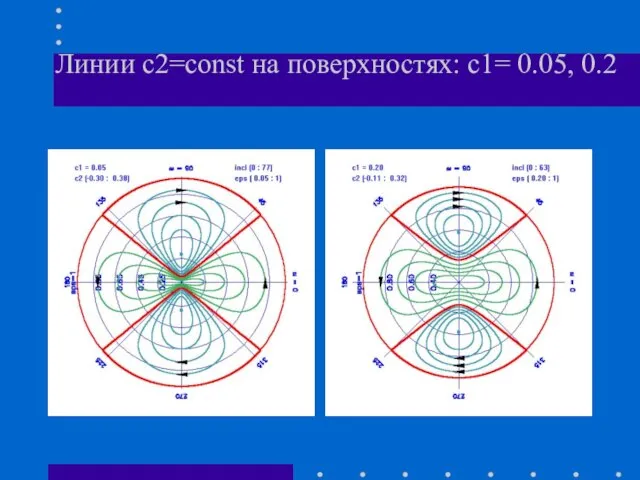
- 13. Линии с2=const на поверхностях: с1= 0.05, 0.2
- 14. Линии с2=const на поверхности с1= 0.4
- 15. Геометрическое исследование эволюции орбит ИСЗ серии ПРОГНОЗ
- 16. Учет конечных размеров центрального тела Баллистическое существование реальных ИСЗ прекращается при их соударении с центральным телом
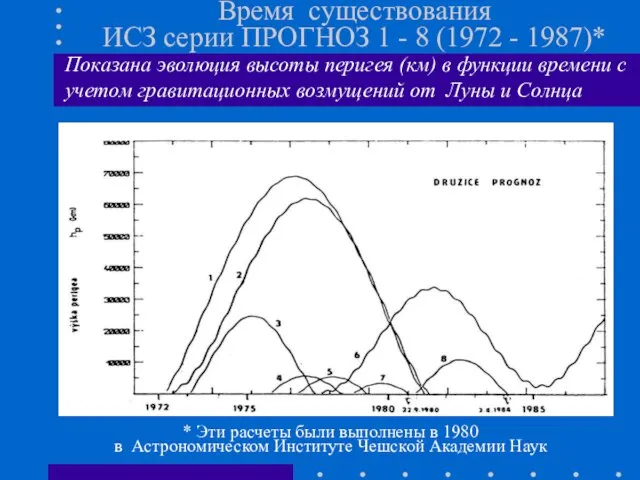
- 17. Время существования ИСЗ серии ПРОГНОЗ 1 - 8 (1972 - 1987)* * Эти расчеты были выполнены
- 18. Соотношения между угловыми элементами орбиты измеряемыми относительно плоскостей земного экватора и эклиптики cos ie = cos
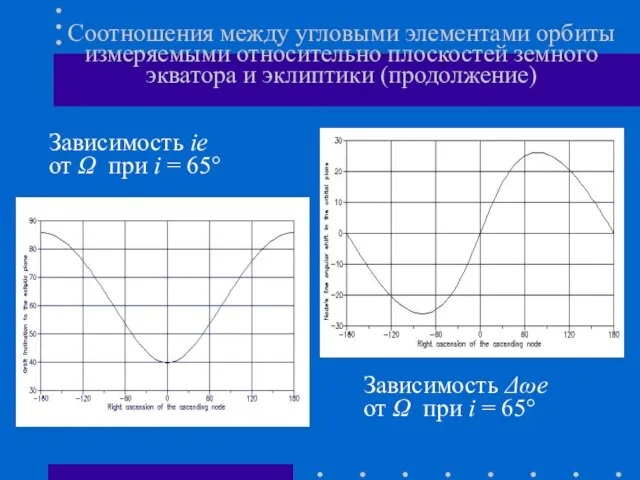
- 19. Соотношения между угловыми элементами орбиты измеряемыми относительно плоскостей земного экватора и эклиптики (продолжение) Зависимость ie от
- 20. Зависимость Ω от долготы точки старта, даты и времени старта Ω = λ + S0 +
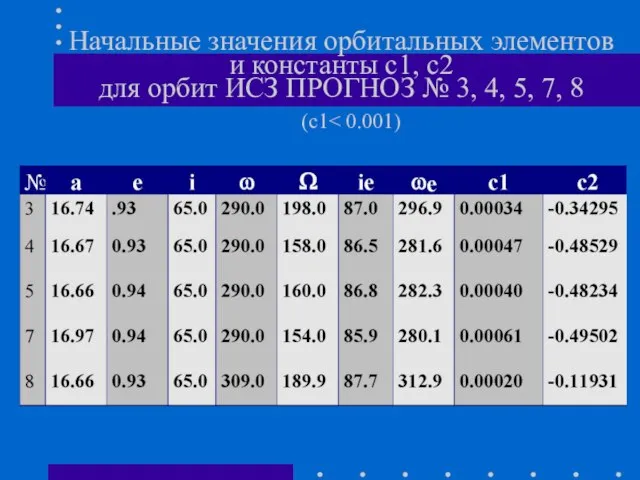
- 21. Начальные значения орбитальных элементов и константы с1, с2 для орбит ИСЗ ПРОГНОЗ № 3, 4, 5,
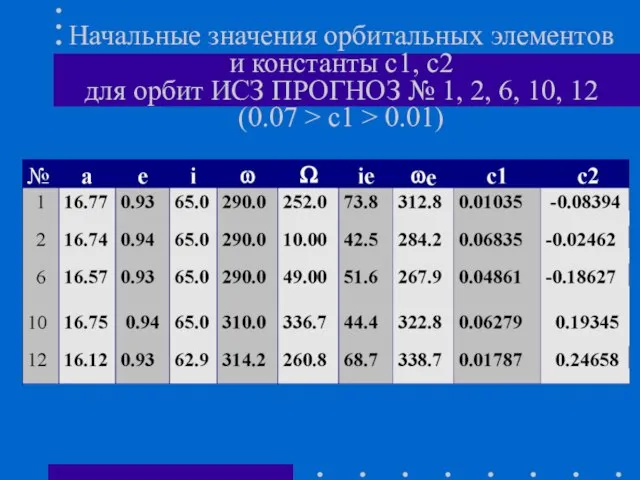
- 22. Начальные значения орбитальных элементов и константы с1, с2 для орбит ИСЗ ПРОГНОЗ № 1, 2, 6,
- 23. Линии с2 для орбит ИСЗ Прогноз 2-8 и 10, объединенных одинаковыми значениями c1 а) с1 =
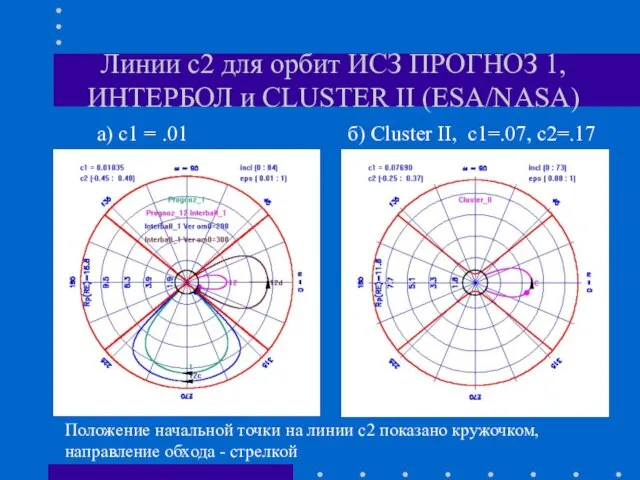
- 24. Линии с2 для орбит ИСЗ ПРОГНОЗ 1, ИНТЕРБОЛ и CLUSTER II (ESA/NASA) а) с1 = .01
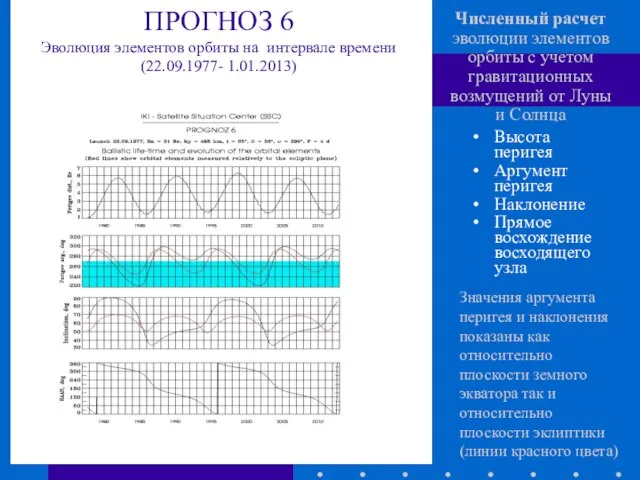
- 25. Высота перигея Аргумент перигея Наклонение Прямое восхождение восходящего узла ПРОГНОЗ 6 Эволюция элементов орбиты на интервале
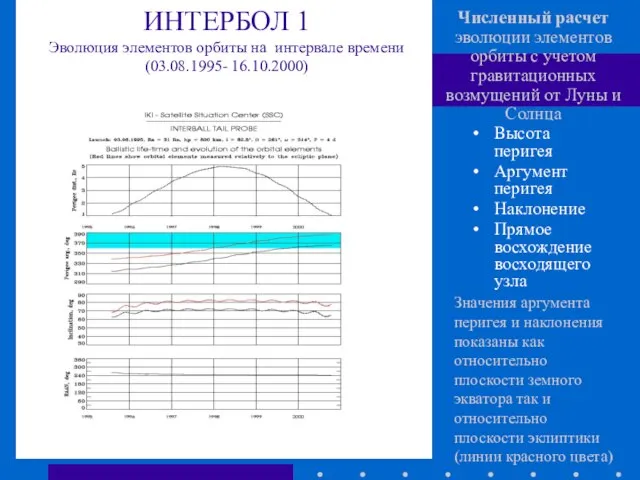
- 26. Высота перигея Аргумент перигея Наклонение Прямое восхождение восходящего узла ИНТЕРБОЛ 1 Эволюция элементов орбиты на интервале
- 27. Заключение Разработан метод геометрического анализа решения ограниченной проблемы трех тел, полученного М.Л. Лидовым. Представлены результаты анализа
- 28. Благодарность Автор считает своим приятным долгом выразить благодарность профессору Б.И. Рабиновичу за ценные советы и полезные
- 30. Скачать презентацию














 Процессы карьеры и социализации. Технология самоорганизации
Процессы карьеры и социализации. Технология самоорганизации Babilonul (Poarta Zeilor)
Babilonul (Poarta Zeilor) Кролики и зайцы
Кролики и зайцы Семинар для специалистов по проведению инструктажа и обеспечению лабораторных работ на экзаменах по физике и химии в 2022 году
Семинар для специалистов по проведению инструктажа и обеспечению лабораторных работ на экзаменах по физике и химии в 2022 году Сочи – зимняя игра, Олимпийская пора
Сочи – зимняя игра, Олимпийская пора Понятие о космосе. Исследование космоса
Понятие о космосе. Исследование космоса Меры социальной поддержки, предоставляемых на территории Курганской области
Меры социальной поддержки, предоставляемых на территории Курганской области Creative agency. Интерактивная встреча по рекламе и PR
Creative agency. Интерактивная встреча по рекламе и PR Аниме. Любимые персонажи
Аниме. Любимые персонажи Воскресение Христово (Пасха)
Воскресение Христово (Пасха) Детское христианское собрание
Детское христианское собрание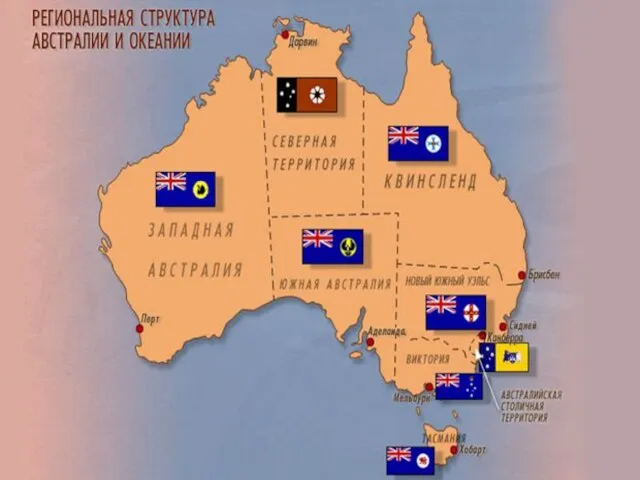 Австралия и Океания.
Австралия и Океания. Открытие республиканского проекта
Открытие республиканского проекта Online стратегии для бизнеса
Online стратегии для бизнеса Скульптура. Проверочная работа
Скульптура. Проверочная работа Игрушка Полкан
Игрушка Полкан Что растёт на клумбе?
Что растёт на клумбе? Органы дыхания и газообмен
Органы дыхания и газообмен Тест Мюнстерберга на восприятие и внимание.
Тест Мюнстерберга на восприятие и внимание. Особенности контрактов на комплектное оборудование Гудимова К. С., Мельник Д.А. гр. МЭ091
Особенности контрактов на комплектное оборудование Гудимова К. С., Мельник Д.А. гр. МЭ091 Русская культура в произведениях русских классиков. Самовар
Русская культура в произведениях русских классиков. Самовар DeVita Ritm mini - цифровое устройство оздоровления
DeVita Ritm mini - цифровое устройство оздоровления Игрушки из носочков своими руками №5
Игрушки из носочков своими руками №5 Буква Я - показатель мягкости согласного
Буква Я - показатель мягкости согласного Требование по размещению рекламных материалов в шинных центрах
Требование по размещению рекламных материалов в шинных центрах Анализ микробиоты кишечника и экспресс-диагностика острых кишечных инфекций методом ПЦР
Анализ микробиоты кишечника и экспресс-диагностика острых кишечных инфекций методом ПЦР Обеспечение исков иностранных граждан, права и обязанности ин лиц
Обеспечение исков иностранных граждан, права и обязанности ин лиц Базовые категории управления
Базовые категории управления