Некоммерческая организация «Ассоциация московских вузов»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИРОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ АГЕ
Содержание
- 2. Тема: ЛОГАРИФМ. Свойства логарифмов..
- 3. ПЛАН ЗАНЯТИЯ. Определение логарифмов. Основное логарифмическое тождество. Свойства логарифмов: - логарифм произведения, частного и степени; -
- 4. Понятие логарифма. Это и есть логарифмы
- 5. Определение логарифма. Логарифмом положительного числа M по основанию a (a > 0, a ̸= 1) называется
- 6. Определение логарифма в виде тождества. Основное логарифмическое тождество.
- 7. ПРИМЕРЫ. , так как 2³=8; 52 = 25;
- 8. в случае, когда M представляет из себя явно некоторую степень a, определение логарифма можно записать так:
- 9. Частные случаи.
- 10. 5 -1 -2 25 0,2 1,5 Самостоятельная работа.
- 11. Свойства логарифмов.
- 12. Свойства логарифмов.
- 13. Примеры: Десятичным логарифмом. называется логарифм, основание которого равно 10. Обозначение: lg M, т.е. lg M=log10 M
- 14. Примеры: Натуральным логарифмом. называется логарифм, основание которого равно e. Обозначение: ln M, т.е. ln M=loge M
- 16. Скачать презентацию







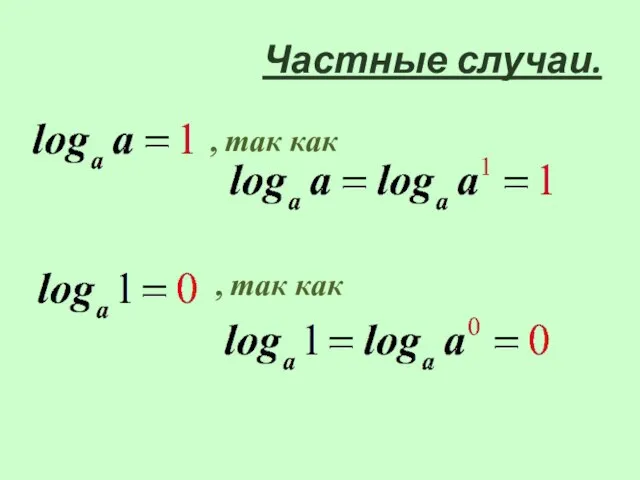





 Материалы для подготовки к контрольной работе по теме Греция
Материалы для подготовки к контрольной работе по теме Греция Управление человеческими ресурсами
Управление человеческими ресурсами Администрирование почтового сервера
Администрирование почтового сервера Загробная жизнь в Древнем Египте: гробницы и саркофаги.
Загробная жизнь в Древнем Египте: гробницы и саркофаги. Учимся письменному пересказу
Учимся письменному пересказу ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года
ОБЩЕСТВЕННАЯ ПАЛАТА ОМСКОЙ ОБЛАСТИ ОБЩЕСТВЕННЫЕ СЛУШАНИЯ «ОБ УСТАНОВКЕ ПАМЯТНИКА А.В. КОЛЧАКУ В г. ОМСКЕ» 19 июля 2012 года  2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап
2.1.1. Содержание и последствия промышленного переворота для мировой экономики. 2.1.2. Англия – родина промышленной революции. 2.1.3. Кап Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого
Отношение к красоте человеческого тела как к великой ценности, данной природой, на протяжении многовековой истории человеческого  Михаил Тариелович Лорис-Меликов
Михаил Тариелович Лорис-Меликов 11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья
11. Четвертый шаг – планирование исследования. Во всяком деле, чтобы добиться успеха, нужна некоторая доля безумия. Шекспир Уилья Презентация на тему Московский Кремль
Презентация на тему Московский Кремль  МК-Малая академия-2019 (новые филиалы без ЛЛ) (4)
МК-Малая академия-2019 (новые филиалы без ЛЛ) (4) Спирты и фенолы
Спирты и фенолы Что такое биомеханика
Что такое биомеханика  Презентация на тему Природная зональность
Презентация на тему Природная зональность  Урок-олимпиада «Кто хочет стать грамотным?»
Урок-олимпиада «Кто хочет стать грамотным?» Анализ социального института собеседования при приеме на работу
Анализ социального института собеседования при приеме на работу Nightrider
Nightrider Г.Цыферов «Как цыплёнок впервые сочинил сказку»
Г.Цыферов «Как цыплёнок впервые сочинил сказку» Якутское национальное блюдо саламат
Якутское национальное блюдо саламат Wildlife of the UK
Wildlife of the UK Что мы знаем о Солнце?
Что мы знаем о Солнце? Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста
Роль баскетбола в развитии физического качества ловкость у учащихся среднего школьного возраста САПР
САПР Компонентная среда разработки инструментария нагрузочного тестирования
Компонентная среда разработки инструментария нагрузочного тестирования Компетентность, универсальные учебные действия и практика проектирования учебного процесса
Компетентность, универсальные учебные действия и практика проектирования учебного процесса Изменение климата
Изменение климата Тема 2.2 Поводження із психічно хворими людьми
Тема 2.2 Поводження із психічно хворими людьми