Геометрия

Содержание
Теорема косинусов
Теорема синусов
Соотношение между углами треугольника и противолежащими сторонами
Решения треугольников
Нажатием мышки выберите нужную тему.
Тест

Теорема косинусов
Теорема 1. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
A
B
C
α
BC ² = AB ² + AC ² - 2AB ▪ AC ▪ cos α
!
!
Далее

Теорема косинусов
Следствие
A
B
C
α
A
B
C
α
D
Угол α - острый
Угол α - тупой
CD – высота
AD – проекция стороны AC на сторону AB.
CD – высота
AD – проекция стороны AC на продолжение стороны AB.
cos α = AD/AC
cos (180 - α) = AD / AC = –cos α
AD = AC ▪ cos α
AD= – AC ▪ cos α
BC ² = AB ² + AC ² – 2AB ▪ AD
BC ² = AB ² + AC ² + 2AB ▪ AD
cos (180 - α) = –cos α
D
Далее
Квадрат стороны треугольника равен сумме квадратов двух других сторон «±» удвоенное произведение одной из них на проекцию другой. Знак «+»надо брать, когда противолежащий угол тупой, а знак «-», когда угол острый.

Теорема косинусов
Далее
Дано:
Найти:
Решение:
AC = 5 м
BC - ?
A
B
C
α
BC ² = AB ² + AC ² - 2AB ▪ AC ▪ cos α
BC ² = 6 ² + 5 ² - 2 ▪ 6 ▪ 5 ▪ 0,6
BC ² = 36 + 25 - 36
BC ² = 25
BC = 5
Ответ: 5 м.
Решение задач - пример № 1.
5
6
?
AB = 6 м
cos α = 0,6

BC ² = AB ² + AC ² - 2AB ▪ AC ▪ cos α
Теорема косинусов
Далее
Дано:
Найти:
Решение:
AC = 5 м
cos α - ?
A
B
C
α
Ответ: 0,2 .
cos α = (AB ² + AC ² - BC ²) / 2AB ▪ AC
cos α = (6 ² + 5 ² - 7 ²) / 2 ▪ 6 ▪ 5
cos α = (36 + 25 - 49) / 60
cos α = 0,2
6
7
5
Решение задач - пример № 2.
AB = 6 м
BC = 7 м

Теорема косинусов
Дано:
Найти:
Решение:
BC = 4 м
AD - ?
BD - ?
A
B
C
α
BC ² = AB ² + AC ² - 2AB ▪ AC ▪ cos α
BC ² = AB ² + AC ² – 2AB ▪ AD
Ответ: AD = 3,75 м; BD = 2,25 м.
D
AD = (AB ² + AC ² – BC ² ) / 2AB
AD = (6 ² + 5 ² – 4 ² ) / 2 ▪ 6
AD = (36 + 25 – 16 ) / 12
AD = 3,75
BD = AB - AD
BD = 6 – 3,75 = 2,25
Возврат в меню
6
5
4
Решение задач - пример № 3.
AC = 5 м
AB = 6 м

Далее
Теорема синусов
Теорема 2. Стороны треугольника пропорциональны синусам противолежащих углов.
A
B
C
α
!
!
A
B
C
α
a/sinα = b/sin β = c/sin γ
a
b
c
a
b
c
β
β
γ
γ

Теорема синусов
Дано:
Найти:
Решение:
 ABC
AB - ?
Ответ: b ▪ sin γ / sin (α + γ)
Далее
A
B
C
α
b
γ
b / sin β = AB / sin γ
AB = b ▪ sin γ / sin β
AB = b ▪ sin γ / sin (180 – (α + γ))
AB = b ▪ sin γ / sin (α + γ)
Решение задач - пример № 1.
AC = b
∠α, ∠ γ
точка B недоступна

Теорема синусов
Возврат в меню
Дано:
Найти:
Решение:
α = 45°
b - ?
A
B
C
α
a
b
c
a/sin α=b/sin β
b= a ▪ sin β/ sin α
b = 3 ▪ sin 60° / sin 45°
β
Решение задач - пример № 2.
β = 60°
a = 3 м

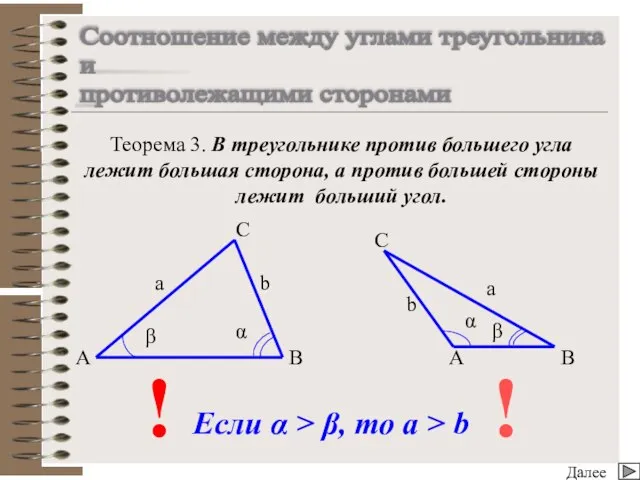
b
α
!
Далее
Соотношение между углами треугольника
и
противолежащими сторонами
Теорема 3. В треугольнике против большего угла лежит большая сторона, а против большей стороны лежит больший угол.
A
B
C
A
B
C
α
a
a
b
β
β
Если α > β, то a > b
!

C
Соотношение между углами треугольника
и
противолежащими сторонами
Далее
Решение задач - пример № 1.
Дано:
Решение:
ABC - равнобедренный
∠A = ∠C > 60°
A
B
∠A = ∠C > 60°
Значит, ∠A + ∠C > 120°
∠B = 180° - (∠A + ∠C) <60°
Следовательно в ABC ∠B – наименьший.
Тогда, согласно соотношению между углами треугольника и его сторонами,AC – наименьшая сторона.
Ответ: AC
Найти:
Что больше AC или AB?

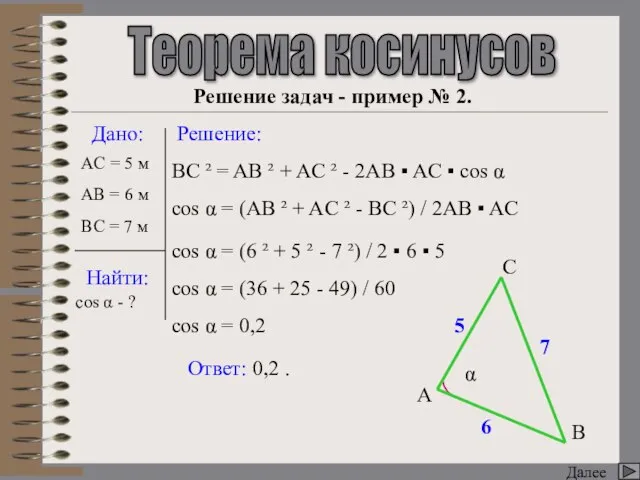
Соотношение между углами треугольника
и
противолежащими сторонами
Возврат в меню
Решение задач - пример № 2.
Дано:
Найти:
Решение:
AC = 18 см
Ответ: ∠A - острый.
Каким является ∠А – острым, прямым или тупым?
A
B
C
18
20
Так как AB > AC, то ∠C > ∠B
То есть ∠С > 50°
Тогда ∠B + ∠C > 100°
∠A = 180° - (∠B + ∠C) > 80°
∠A - острый
50°
AB = 20 см
∠B = 50°
?

c = 20 ▪ (sin 45° / sin 75°) ≈ 20 ▪ (0,7 / 0,966) ≈ 14,6
Далее
Решения треугольников
Решение задач - пример № 1.
Дано:
Найти:
Решение:
a = 20 см
Ответ: 45°; 17,9 см; 14,6 см.
∠ γ - ?
b - ?
c - ?
γ = 180° - (β + α)
γ = 180° - (75° + 60°) = 45°
b = a ▪ (sin β / sin γ)
с
a
α
b
β
γ
b = 20 ▪ (sin 60° / sin 75°) ≈ 20 ▪ (0,866 / 0,966) ≈ 17,9
c = a ▪ (sin γ / sin α)
a / sin α = b / sin β = c / sin γ
∠ α = 75 °
∠ β = 60°

γ
Далее
Решения треугольников
Решение задач - пример № 2.
Дано:
Найти:
Решение:
Ответ: 28 см; 39°; 11°.
cos α = (b ² + c ² - a ²) / 2 ▪ b ▪ c
cos α = (529 + 784 – 49) / 2 ▪ 23 ▪ 28 ≈ 0,981
∠α ≈ 11°
a = 7 м
a
α
b
β
c
∠α - ?
∠β - ?
c - ?
∠β =180° - (α + γ) = 180° - (11° + 130°) ≈ 39°
b = 23 м
∠ γ = 130°

Решения треугольников
Решение задач - пример № 3.
Далее
Дано:
Найти:
Решение:
a = 7 см
Ответ: 54°; 13°; 113°.
∠α - ?
β - ?
∠γ - ?
cos α = (b ² + c ² - a ²) / 2 ▪ b ▪ c
cos α = (4 + 64 – 49) / 2 ▪ 2 ▪ 8 ≈ 0,981
∠α ≈ 54°
∠γ ≈ 180° - (α + β) = 180° - (54° + 13°) = 113°
cos β = (a ² + c ² - b ²) / 2 ▪ a ▪ c
cos β = (49 + 64 – 4) / 2 ▪ 7 ▪ 8 ≈ 0,973
∠β ≈ 13°
γ
a
α
b
β
c
b = 2 см
c = 8 см

Решения треугольников
Решение задач - пример № 4.
Далее
Дано:
Найти:
Решение:
a = 12 см
Ответ: 8,69 см; 21°; 39°.
c - ?
β - ?
∠γ - ?
a / sin α = b / sin β = c / sin γ
sin β = (b / a) ▪ sin α
∠β1 ≈ 21° и ∠β2 ≈ 159°, так как ∠α - тупой, а в треугольнике может быть только один тупой угол, то ∠β ≈ 21°.
∠γ ≈ 180° - (α + β) = 180° - (120° + 21°) = 39°
γ
a
α
b
β
c
sin β = (5 / 12) ▪ 0,866 ≈ 0,361
c = 12 ▪ (sin 39° / sin 120°) ≈ 12 ▪ (0,629 / 0,866) ≈ 8,69
c = a ▪ (sin γ / sin α)
b = 5 см
∠α = 120°