Гидроэнергетика

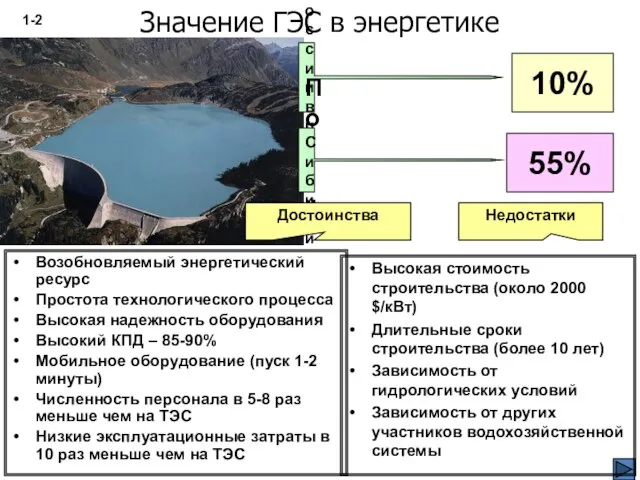
Значение ГЭС в энергетике
По России в целом
По Сибири
10%
55%
1-
Возобновляемый энергетический ресурс
Простота технологического процесса
Высокая надежность оборудования
Высокий КПД – 85-90%
Мобильное оборудование (пуск 1-2 минуты)
Численность персонала в 5-8 раз меньше чем на ТЭС
Низкие эксплуатационные затраты в 10 раз меньше чем на ТЭС
Высокая стоимость строительства (около 2000 $/кВт)
Длительные сроки строительства (более 10 лет)
Зависимость от гидрологических условий
Зависимость от других участников водохозяйственной системы
Достоинства
Недостатки

Цели и задачи раздела
Основные темы раздела:
Основные законы гидравлики
Гидроэнергетические ресурсы и схемы их использования
Водноэнергетические показатели ГЭС
Водноэнергетическое регулирование водохранилищ
Участники водохозяйственного комплекса и их интересы
Технологическая схема преобразования гидравлической энергии в электрическую
Энергетические характеристики гидроагрегатов и ГЭС в целом
Гидротехнические сооружения гидроузлов
1-
Цель данного раздела - изучение: физико-технических основ преобразования первичной гидроэнергетических ресурсов в электрическую энергию и основных технологических схем.
Знакомство с отдельными типовыми конструктивными элементами, характеризующих технологический процесс преобразования и определяющих экономические показатели станции.

Основные законы гидравлики
Тема II-1
1-
Курс «Гидроэнергетика»

тема: Основные законы гидравлики
План лекции
Физико-технические свойства энергоносителя.
Показатели и параметры характеризующие энергоноситель.
Основные законы гидравлики.
Энергетическое уравнение Бернулли для жидкости.
1-

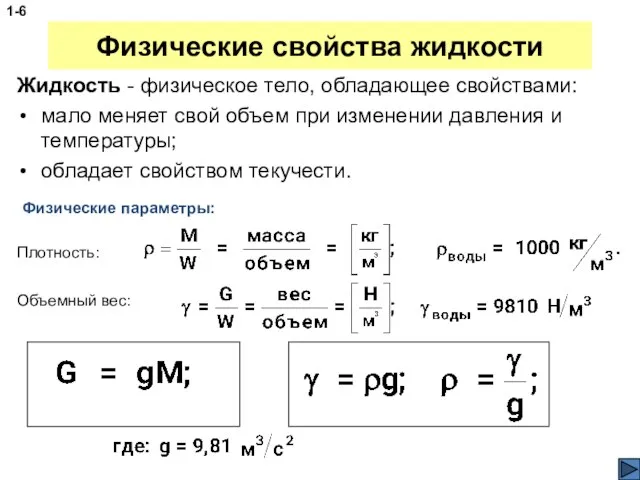
Физические свойства жидкости
Жидкость - физическое тело, обладающее свойствами:
мало меняет свой объем при изменении давления и температуры;
обладает свойством текучести.
1-
Физические параметры:

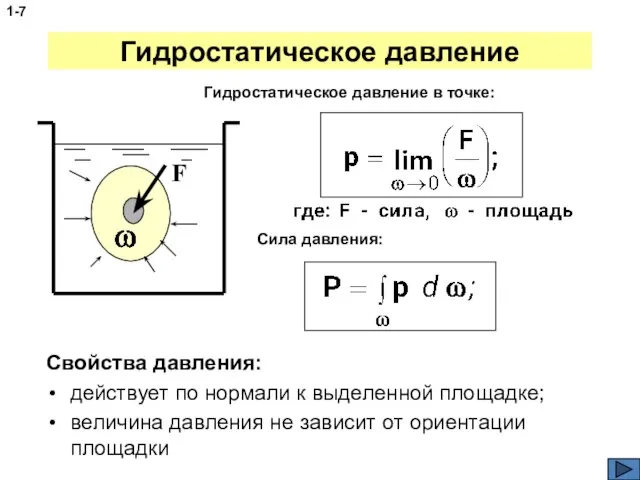
Гидростатическое давление
Свойства давления:
действует по нормали к выделенной площадке;
величина давления не зависит от ориентации площадки
1-

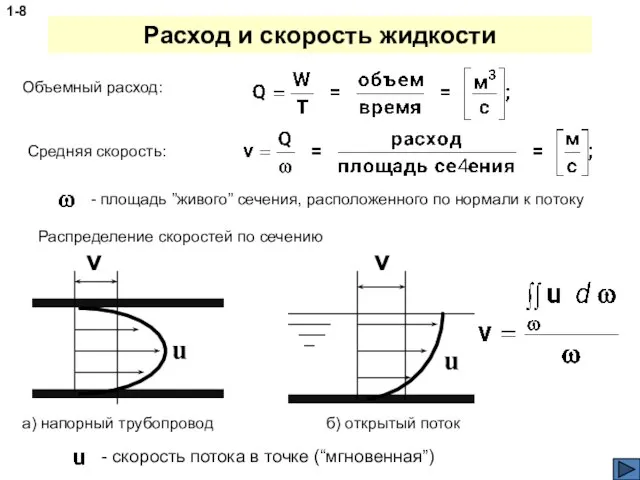
Расход и скорость жидкости
1-

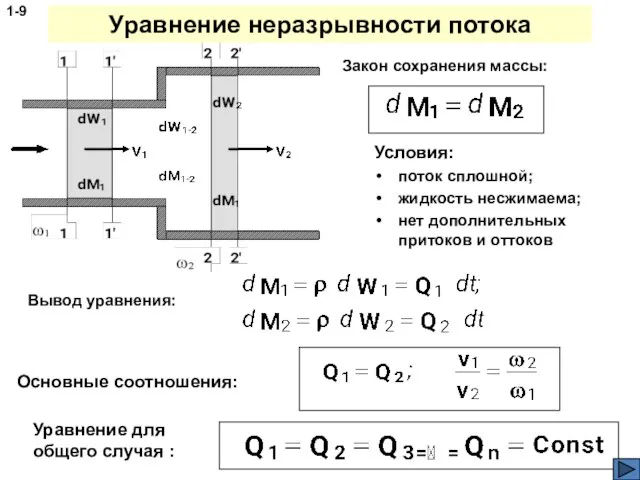
Уравнение неразрывности потока
Условия:
поток сплошной;
жидкость несжимаема;
нет дополнительных притоков и оттоков
1-

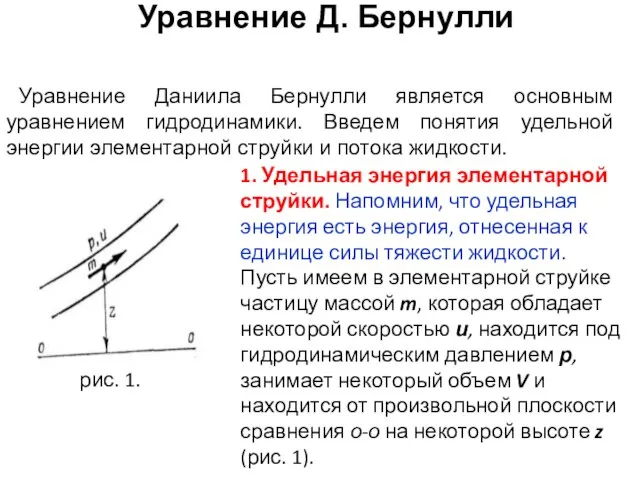
Уравнение Д. Бернулли
Уравнение Даниила Бернулли является основным уравнением гидродинамики. Введем понятия удельной энергии элементарной струйки и потока жидкости.
1. Удельная энергия элементарной струйки. Напомним, что удельная энергия есть энергия, отнесенная к единице силы тяжести жидкости. Пусть имеем в элементарной струйке частицу массой m, которая обладает некоторой скоростью и, находится под гидродинамическим давлением р, занимает некоторый объем V и находится от произвольной плоскости сравнения о-о на некоторой высоте z (рис. 1).

Масса частицы обладает запасом удельной потенциальной энергии еп, которая складывается из удельных потенциальных энергий положения епол, и давления едав.
В самом деле, масса жидкости, поднятая на высоту z, имеет запас потенциальной энергии, равный mgz, где g – ускорение свободного падения.
Удельная потенциальная энергия положения равна потенциальной энергии, деленной на силу тяжести жидкости (mg)

Масса жидкости занимает некоторый объем V, находящийся под давлением р.
Потенциальная энергия давления равна рV.
Удельная же потенциальная энергия давления равна потенциальной энергии pV, деленной на силу тяжести данного объема γV, т.е.
Полный запас удельной потенциальной энергии массы жидкости равен их сумме, т. е.
(1)

Кроме того, масса жидкости т движется со скоростью и и обладает кинетической энергией
но сила тяжести этой массы равна mg, и удельная кинетическая энергия струйки равна
Складывая выражения (1) и (2), получим выражение полной удельной энергии элементарной струйки
(2)
(3)

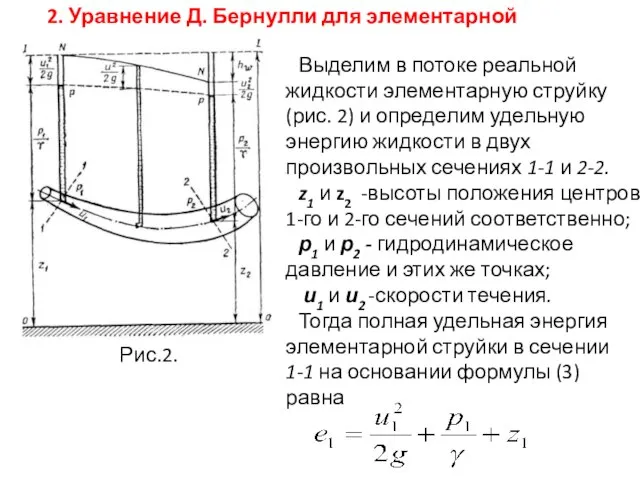
2. Уравнение Д. Бернулли для элементарной струйки.
Выделим в потоке реальной жидкости элементарную струйку (рис. 2) и определим удельную энергию жидкости в двух произвольных сечениях 1-1 и 2-2.
z1 и z2 -высоты положения центров 1-го и 2-го сечений соответственно;
р1 и р2 - гидродинамическое давление и этих же точках;
и1 и и2 -скорости течения.
Тогда полная удельная энергия элементарной струйки в сечении 1-1 на основании формулы (3) равна

а в сечении 2-2
Практически всегда
так как часть полной энергии затрачивается на преодоление сил сопротивления (трения) при движении жидкости от сечения 1-1 к сечению 2-2. Обозначим эти потери
Тогда в соответствии с законом сохранения энергии можно написать, что
Это и есть уравнение Бернулли для элементарной струйки

3. Уравнение Д. Бернулли для потока
Поток жидкости рассматривается как совокупность п элементарных струек, каждая из которых обладает своей удельной кинетической энергией u2/2g.
Cреднее значение этой величины в сечении потока будет равно:
Здесь α – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии).
Безразмерный коэффициент α представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости.

В практических расчетах обычно принимают α=1,0 .
Тогда формула Бернулли упрощается:
v1 и v2 – средние скорости в сечениях 1-1 и 2-2.
α1 и α2 – коэффициенты Кориолиса по сечениям. Обычно принимают α1 = α2 = α.
На основе обработки многочисленных данных, полученных на реках и каналах, установлено, что для больших открытых потоков α≈1,1 . При равномерном движении в трубах и каналах практически α≈1,0 ÷ 1,5 .
Тогда уравнение Бернулли для потока в сечениях 1 и 2 будет выглядеть следующим образом: