Содержание
- 2. Лекция 6. ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ И АППАРАТЫ. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ. УРАВНЕНИЕ БЕРНУЛЛИ
- 3. 1.ВВЕДЕНИЕ 2. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ 3. ДАВЛЕНИЕ ПОКОЯЩЕЙСЯ ЖИДКОСТИ НА ДНО И СТЕНКИ СОСУДА 4.ГИДРОСТАТИЧЕСКИЕ МАШИНЫ
- 4. 1. ВВЕДЕНИЕ Проведение процессов химической технологии обычно связано с перемещением жидкостей, газов или паров в трубопроводах
- 5. В гидростатике изучается равновесие жидкостей, находящихся в состоянии относительного покоя. При этом форма объема жидкости не
- 6. Разделив левую и правую части уравнения на ρg и умножив все его члены на (-1), получим:
- 7. Для двух произвольных горизонтальных плоскостей I – I и II – II (рисунок 1) уравнение примет
- 8. Величину p / (ρ g) называют гидростатическим или пьезометрическим напором. Как и нивелирная высота, гидростатический напор
- 9. Переписав уравнение относительно p2, получим: Уравнение (54) является выражением закона Паскаля, из которого следует, что давление,
- 10. Давление жидкости на горизонтальное дно сосуда везде одинаково. Давление же на его боковые стенки возрастает с
- 11. Поскольку гидростатическое давление жидкости на вертикальную стенку сосуда изменяется по ее высоте, то общая сила давления
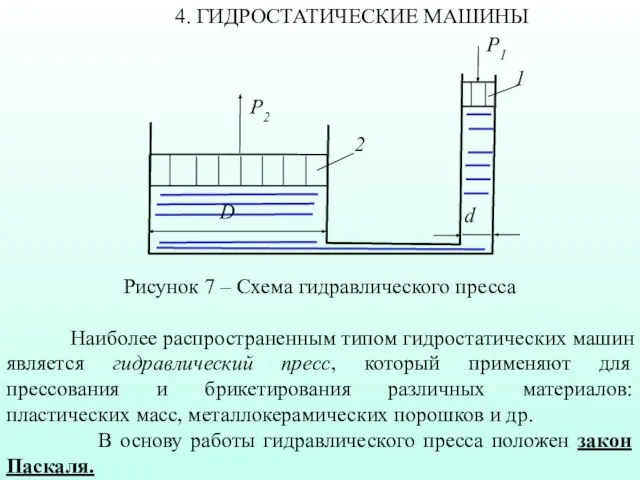
- 12. 4. ГИДРОСТАТИЧЕСКИЕ МАШИНЫ Рисунок 7 – Схема гидравлического пресса Наиболее распространенным типом гидростатических машин является гидравлический
- 13. При приложении сравнительно небольшого усилия к поршню 1 (рисунок 7), движущемуся в цилиндре меньшего диаметра d,
- 14. При преобразовании уравнения Навье-Стокса для идеальной жидкости была получена система уравнений: которые называют дифференциальными уравнениями движения
- 15. Для того чтобы найти силы, действующие во всем рассматриваемом объеме движущейся идеальной жидкости, умножим левые и
- 16. Сложим левые и правые части этих уравнений. Получим уравнение (57): В правой части уравнения (57) выражение,
- 17. С учетом проведенных преобразований уравнение (57) примет вид: Так как в рассматриваемом случае ρ = const
- 18. Очевидно, что для любых сечений потока значение Н должно оставаться постоянным, т. е.: Сумма z +
- 20. Скачать презентацию
















 ВодорастворимыеРастительныеМасла (ВРМ)
ВодорастворимыеРастительныеМасла (ВРМ) Областные особенности русского костюма
Областные особенности русского костюма Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация
Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация Панели стеновые CPL
Панели стеновые CPL Подготовка к ЕГЭ. Решение задач на движение
Подготовка к ЕГЭ. Решение задач на движение Презентация замороженных фруктовых пюре и ягод Dira
Презентация замороженных фруктовых пюре и ягод Dira Зеленый наряд нашего города
Зеленый наряд нашего города Техника квиллинг
Техника квиллинг «Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос
«Атлас флоры и фауны Белого моря» это коллективная монография, подготовленная большой группой специалистов. Книга дает возможнос Текхнология блокчейн: инвестиции в будущее
Текхнология блокчейн: инвестиции в будущее Выгода открытия бизнеса в 2020 году
Выгода открытия бизнеса в 2020 году Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word
Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word Романтизм в русской живописи XIX века
Романтизм в русской живописи XIX века Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл
Развитие методов синтеза, исследование физико-химических и электрофизических свойств модифицированных наноуглеродных и фторугл Профи-digest
Профи-digest lecture_5
lecture_5 Виды сказуемых
Виды сказуемых Radiographic Interpretation of Infections of Jaws
Radiographic Interpretation of Infections of Jaws phpm2fa0e_ovosibirskaya-oblast
phpm2fa0e_ovosibirskaya-oblast Итоги 2-й четверти
Итоги 2-й четверти Математика-царица наук?
Математика-царица наук? Экономический смысл налогообложения
Экономический смысл налогообложения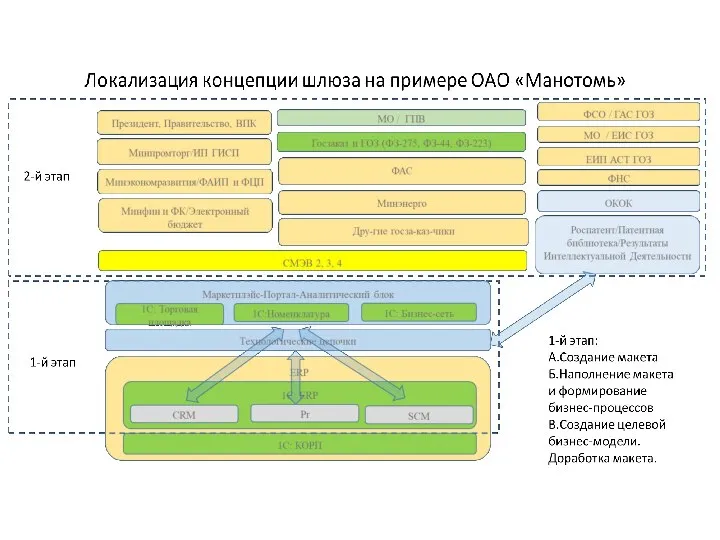 Локализация концепции шлюза на примере ОАО Манотомь
Локализация концепции шлюза на примере ОАО Манотомь Презентация на тему Справедливость и равенство
Презентация на тему Справедливость и равенство Protection of environment
Protection of environment Статусы пассажиров. Служебные пассажиры
Статусы пассажиров. Служебные пассажиры Буквы Ч и Щ в суффиксах имён существительных
Буквы Ч и Щ в суффиксах имён существительных Отдыхаем на отлично
Отдыхаем на отлично