Содержание
- 2. Переход по слайдам осуществляется только по нажатию левой кнопки мыши клик мыши!!! Если есть мигающая стрелка,
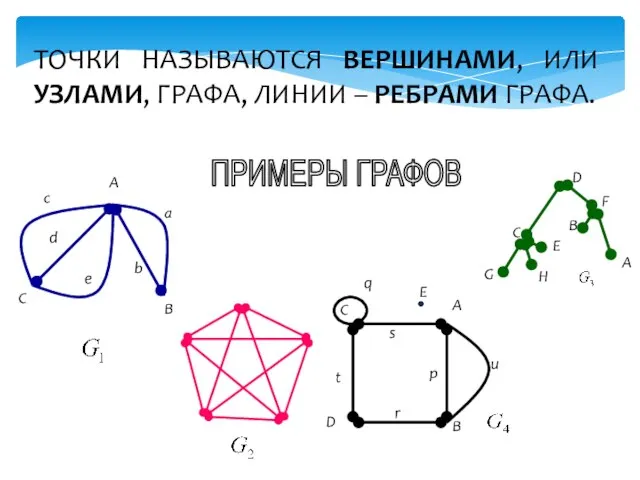
- 3. ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ
- 4. ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА. ПРИМЕРЫ ГРАФОВ
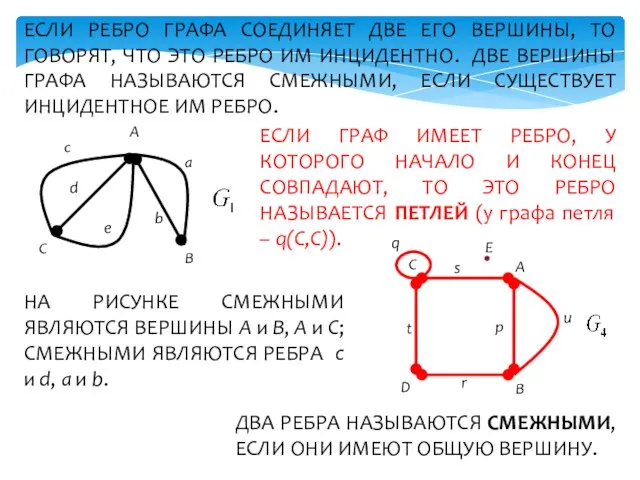
- 5. ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ
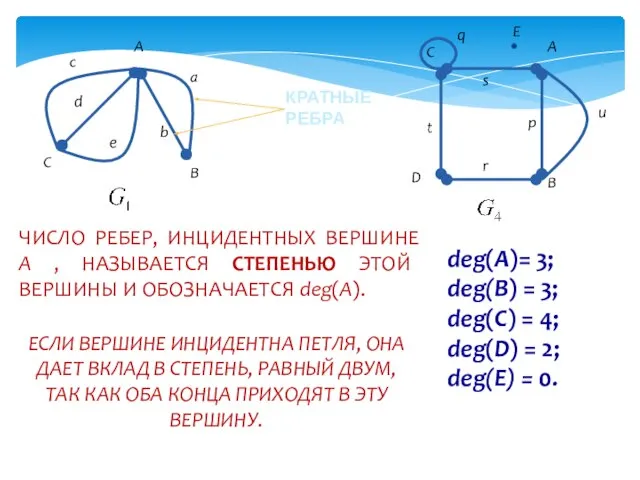
- 6. КРАТНЫЕ РЕБРА ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A). deg(A)=
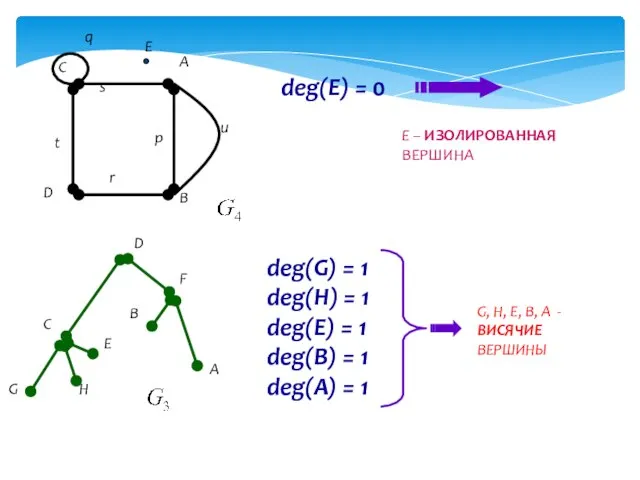
- 7. deg(E) = 0 E – ИЗОЛИРОВАННАЯ ВЕРШИНА deg(G) = 1 deg(H) = 1 deg(E) = 1
- 8. ТЕОРЕМА В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ
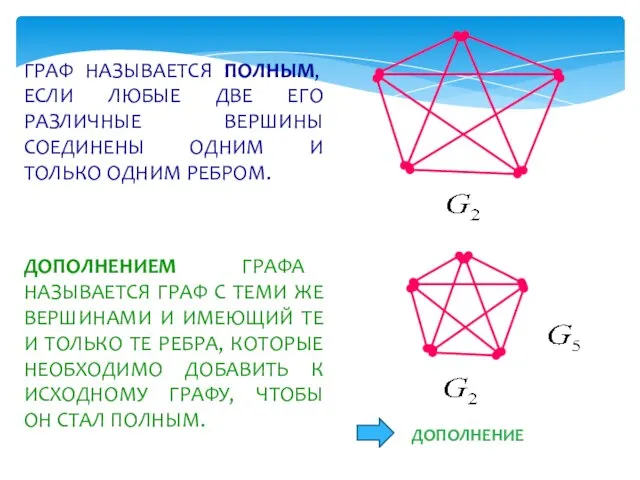
- 9. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ. ДОПОЛНЕНИЕМ
- 10. ДУГИ НАЧАЛО ДУГИ (A,B) КОНЕЦ ДУГИ (A,B) СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ ЧИСЛО РЕБЕР, ДЛЯ
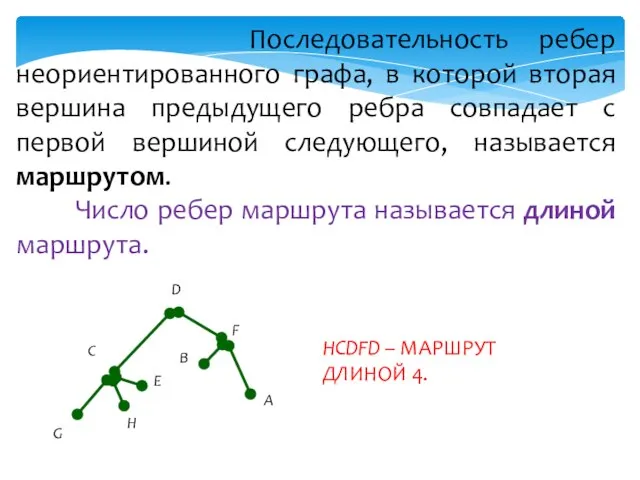
- 11. Последовательность ребер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего, называется
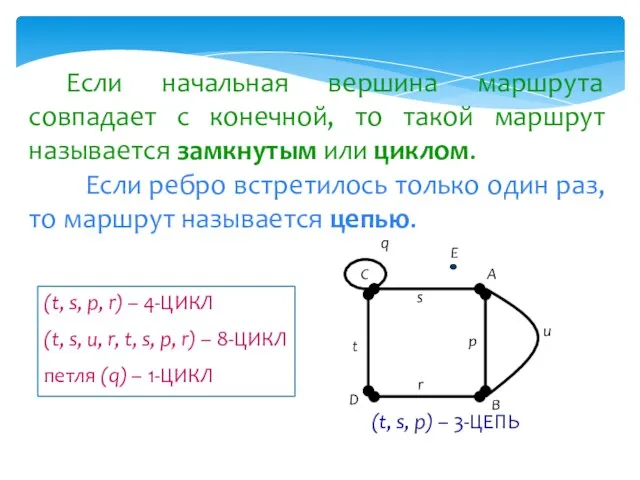
- 12. Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутым или циклом. Если ребро
- 13. совпадает с началом следующего и все ребра единственны. ЦИКЛ В ОРГРАФЕ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ
- 14. ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ
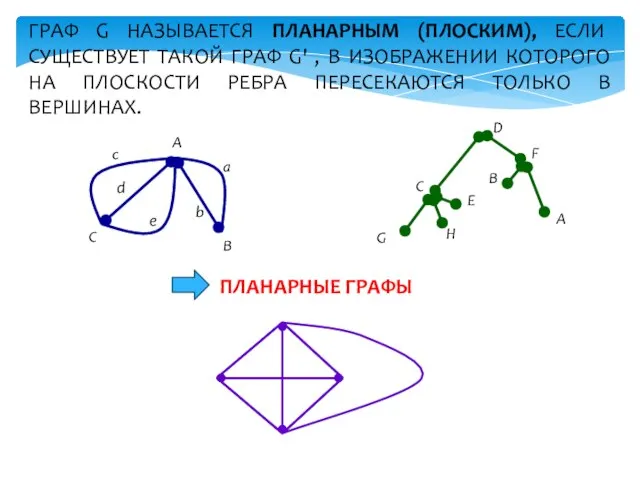
- 15. ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ (ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' , В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ
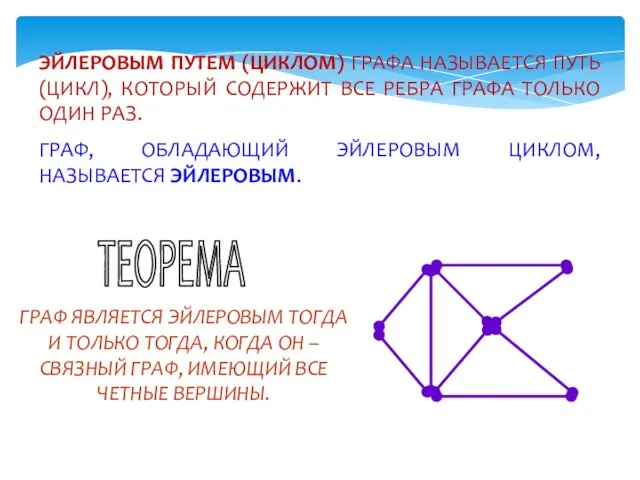
- 16. ЭЙЛЕРОВЫМ ПУТЕМ (ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ (ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА ТОЛЬКО ОДИН РАЗ. ГРАФ,
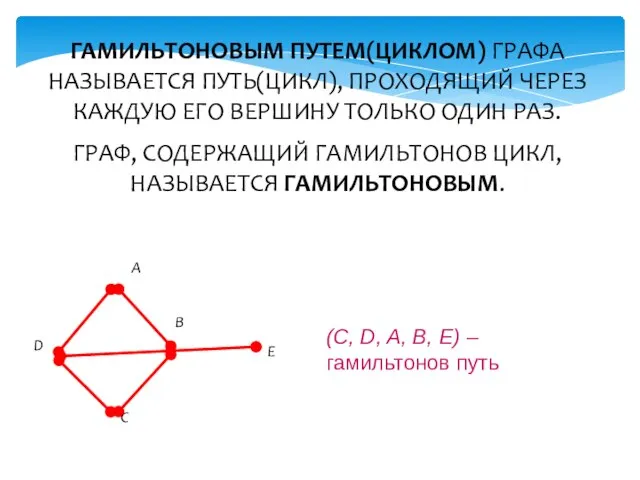
- 17. ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО ОДИН РАЗ. ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ
- 18. МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:
- 19. МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ A ПОРЯДКА n, В КОТОРОЙ: aij
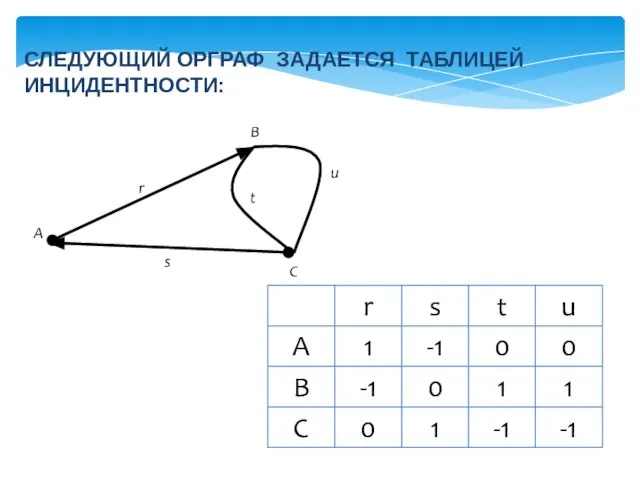
- 20. СЛЕДУЮЩИЙ ОРГРАФ ЗАДАЕТСЯ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ:
- 22. Скачать презентацию







 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)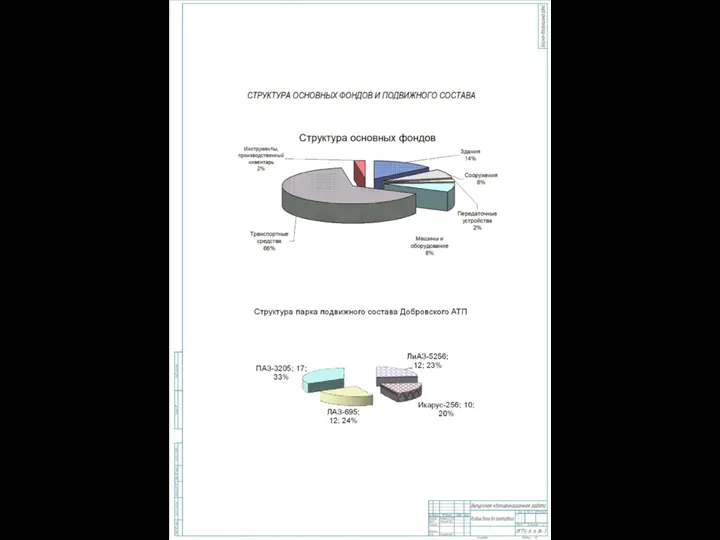 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС