Слайд 8Метод проекций.
Аппарат проецирования

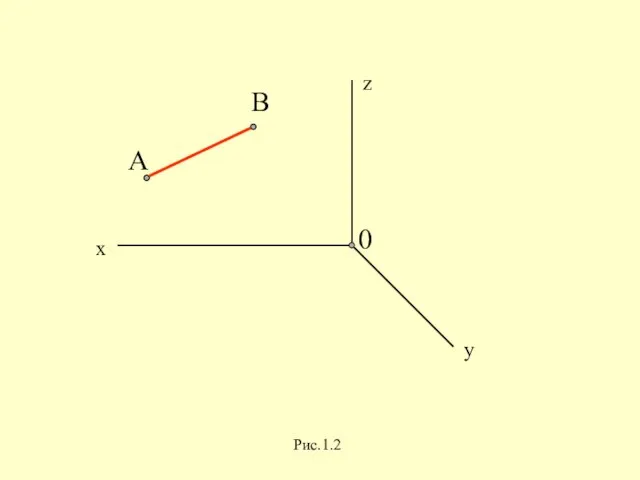
Слайд 9Проецирование - это построение
изображения объекта на плоскости
при помощи проецирующих
лучей, исходящих из одной

точки (центра)
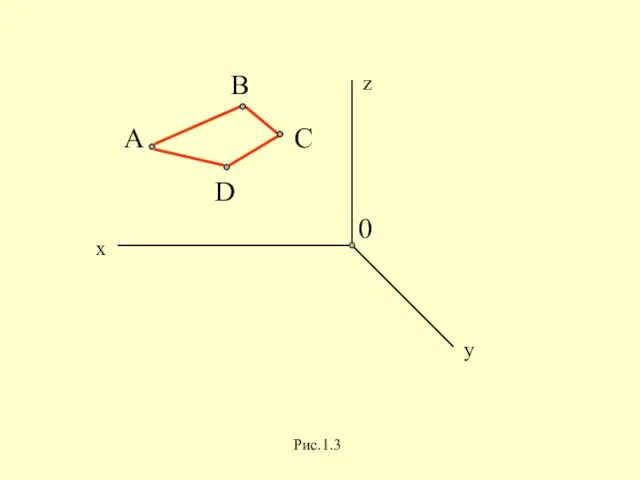
Слайд 10 Полученное изображение - проекция.
Плоскость,на которую падают
проецирующие лучи -
плоскость проекций.

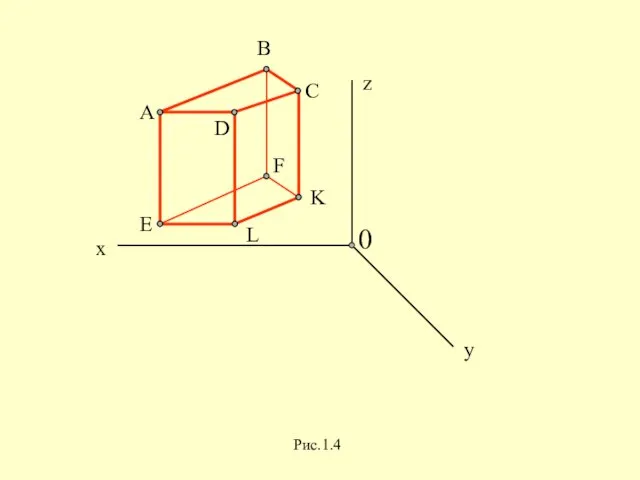
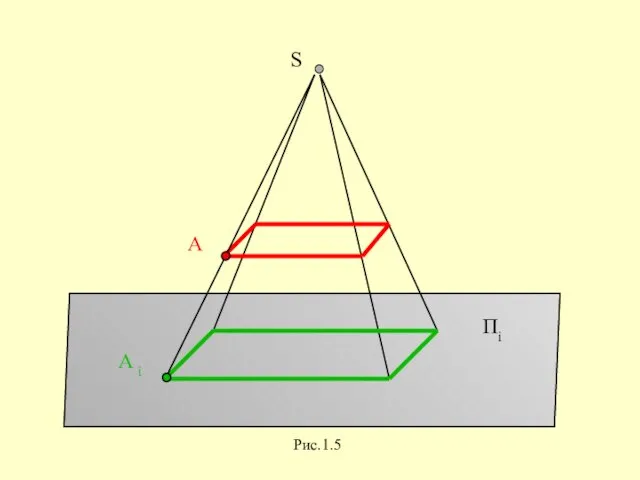
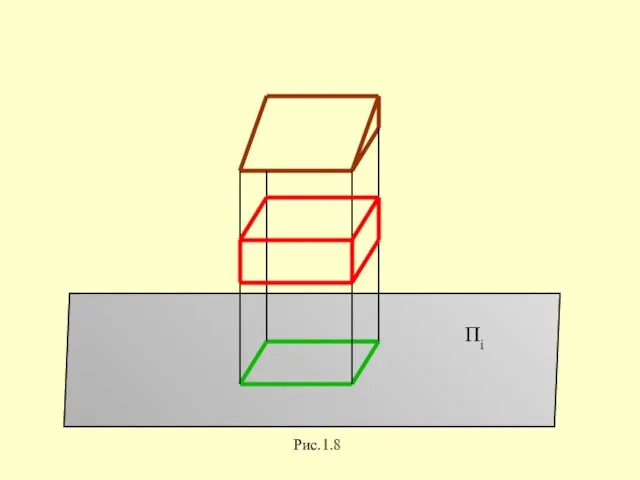
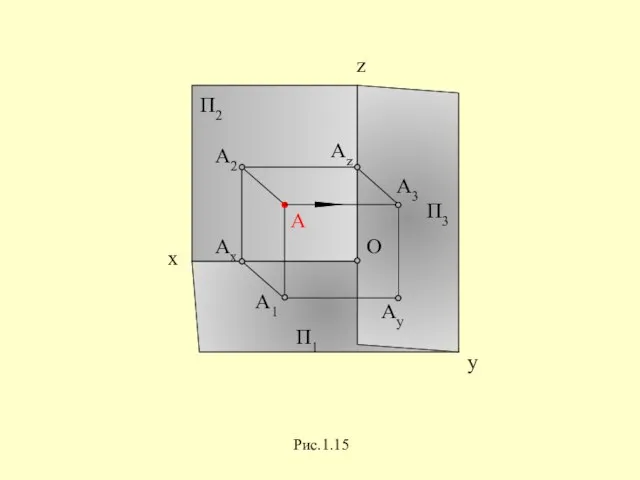
Слайд 12Аппарат проецирования включает в себя:
Пi - плоскость проекций,
S - центр проецирования,
А -

объект проецирования (точка),
SA - проецирующую прямую,
Ai - проекцию точки А.
Слайд 14Пi
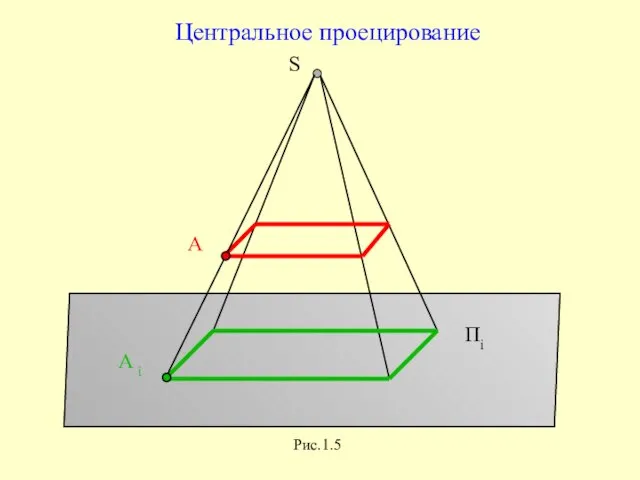
Центральное проецирование
Рис.1.5
Слайд 15Пi
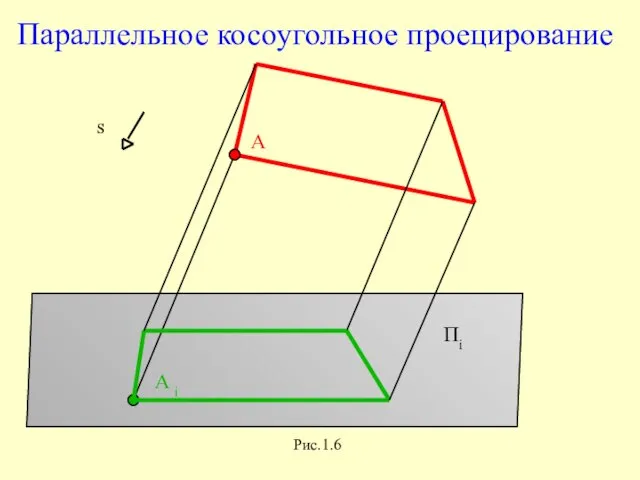
Параллельное косоугольное проецирование
Рис.1.6
Слайд 16Пi
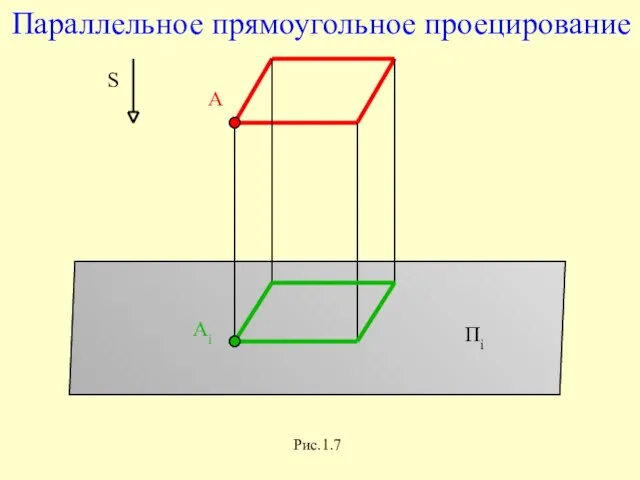
Параллельное прямоугольное проецирование
Рис.1.7
Слайд 17Обратимость изображений объектов пространства

Слайд 20 Обратимость изображений под-разумевает возможность однознач-ного представления формы, размеров и расположения предмета в

пространстве
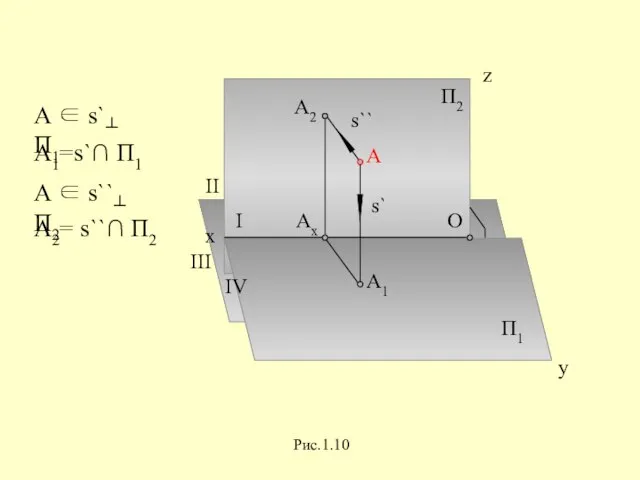
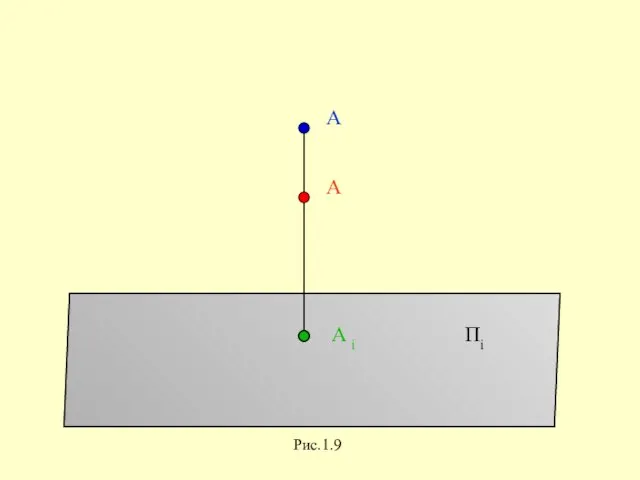
Слайд 21Образование чертежа точки в системе двух плоскостей проекций

Слайд 22A ∈ s`┴ П1
А1=s`∩ П1
A2= s``∩ П2
A ∈ s``┴ П2
Рис.1.10
Слайд 23A2
A1
s` ┴ П1
s`` ┴ П2
s` ∩ s`` = A
Рис.1.11
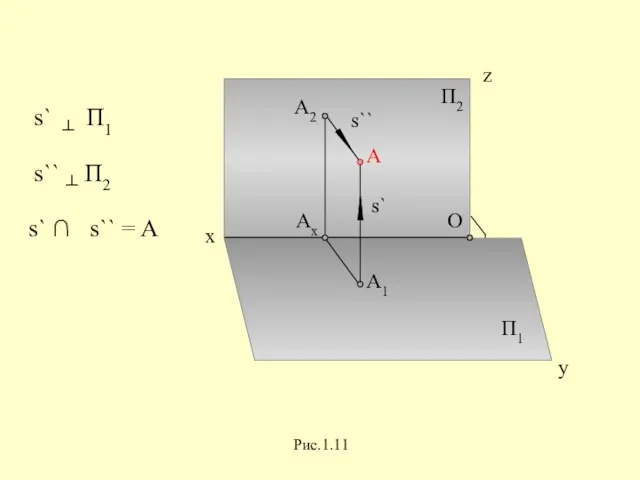
Слайд 24 Две проекции точки вполне определяют ее положение в пространстве относительно данной системы

плоскостей проекций
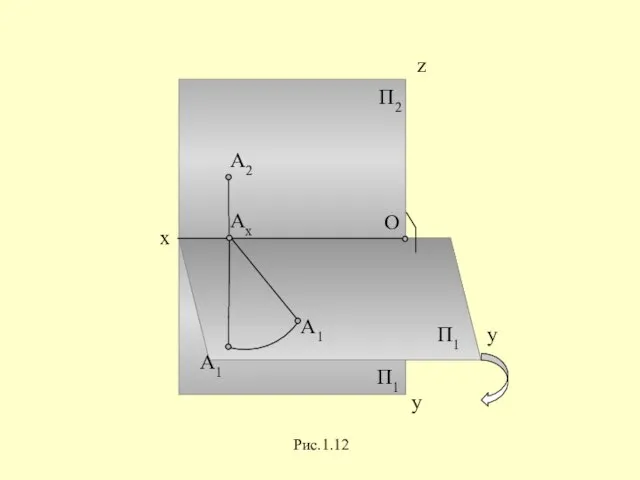
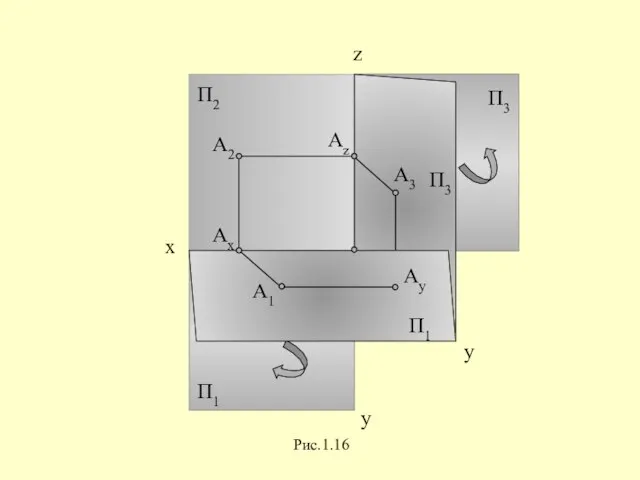
Слайд 26В результате указанного совмещения плоскостей П2 и П1 получается чертеж, известный под

названием эпюр Монжа или двухкартинный чертеж, включающий две взаимосвязанные проекции - “картины”
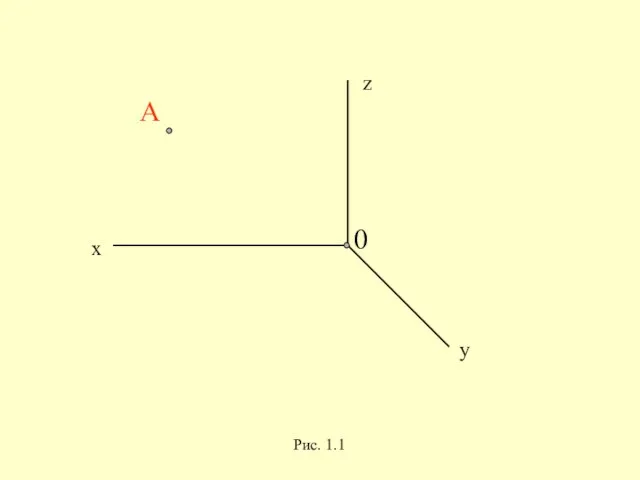
Слайд 27A2
z
Ax
A1
1. [О Ах]
3. [Ах А1]
4. [AxA2]
2. ┴
Рис.1.13
![A2 z Ax A1 1. [О Ах] 3. [Ах А1] 4. [AxA2] 2. ┴ Рис.1.13](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/839133/slide-26.jpg)
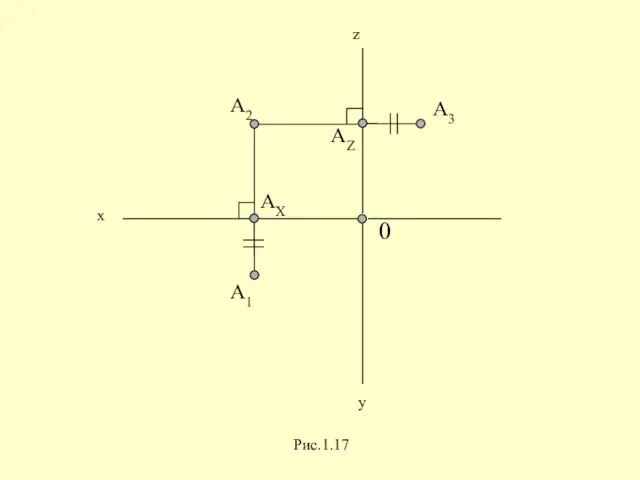
Слайд 32Выводы:
Каждая точка пространства характеризуется тремя координатами: А (х, у, z).
Каждая проекция точки

на чертеже – двумя координатами: А1 (х, у); А2 (х, z); А3 (у, z).
Две проекции точки однозначно определяют ее положение в пространстве.
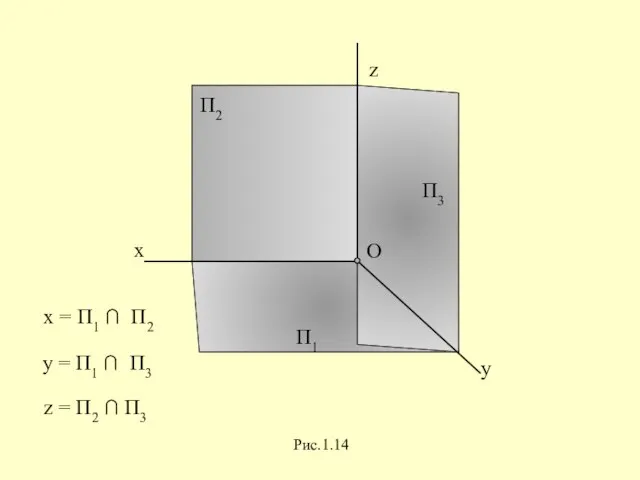
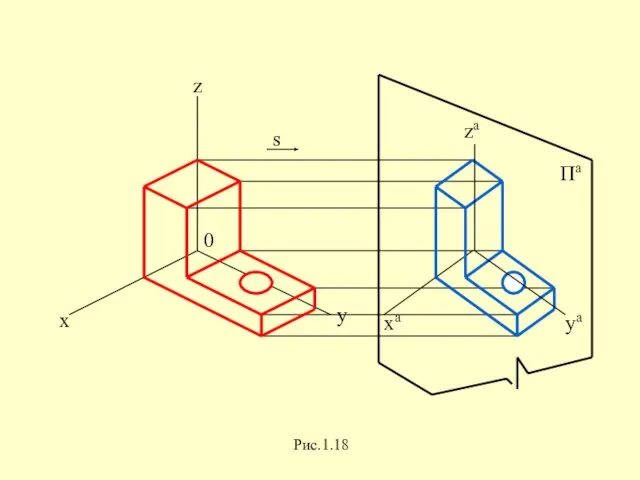
Слайд 33Образование
аксонометрического чертежа точки

Слайд 34 Однокартинный чертеж, обладающий
свойствами наглядности и обратимости,
называется аксонометрическим

Слайд 36x y z - натуральная система координат
Пa - аксонометрическая плоскость проекций
xa ya

za - аксонометрическая система координат
s - направление проецирования
Слайд 37х
z
y
za
ya
xa
A1
A
Ax
ex
ey
ez
A1a
Aa
Axa
eza
eya
exa
0
0a
Пa
ех = еу = еz = е - натуральная единица
Рис.1.19
А1а – вторичная
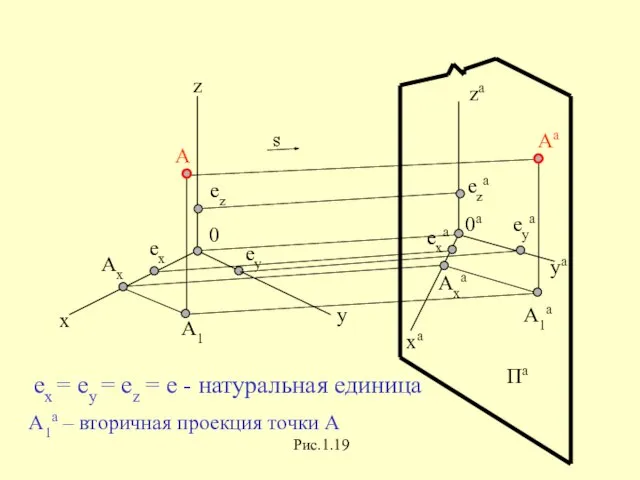
проекция точки А
Слайд 38x
z
y
120°
90°
30°
Прямоугольная изометрическая проекция
Рис.1.20
О
кх = ку = кz ≈ 1

Слайд 397°10'
z
90°
41°25'
0
Прямоугольная диметрическая проекция
кх = кz ≈ 1; ky ≈ 0,5
х
у
Рис.1.21

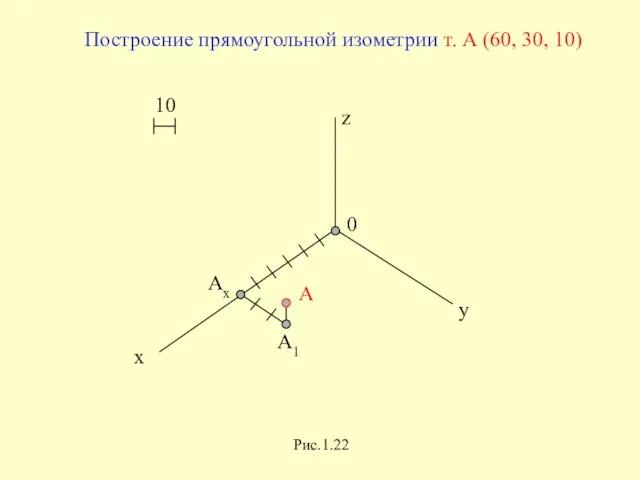
Слайд 40y
x
0
z
Рис.1.22
Построение прямоугольной изометрии т. А (60, 30, 10)

















![A2 z Ax A1 1. [О Ах] 3. [Ах А1] 4. [AxA2] 2. ┴ Рис.1.13](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/839133/slide-26.jpg)








 Обустройство места отдыха Песковатка
Обустройство места отдыха Песковатка Символы и символика г.о. Новокуйбышевск
Символы и символика г.о. Новокуйбышевск Элективный курс «Имидж и этикет современного делового человека»
Элективный курс «Имидж и этикет современного делового человека» Ребёнок и компьютер
Ребёнок и компьютер СТЕРОИДЫ
СТЕРОИДЫ Успешное размещение информационных материалов в СМИ. Право неприменения ККТ при разных способах расчета
Успешное размещение информационных материалов в СМИ. Право неприменения ККТ при разных способах расчета ФУНКЦИОНАЛЬНО-ЦЕЛЕВАЯ СТРУКТУРА ОРГАНОВ ИСПОЛНИТЕЛЬНОЙ ВЛАСТИ ОБЛАСТИ
ФУНКЦИОНАЛЬНО-ЦЕЛЕВАЯ СТРУКТУРА ОРГАНОВ ИСПОЛНИТЕЛЬНОЙ ВЛАСТИ ОБЛАСТИ Стили планирования
Стили планирования Мифология Древнего Египта
Мифология Древнего Египта Эволюция биологических систем и проблема построения «сильного» (динамического) искусственного интеллекта
Эволюция биологических систем и проблема построения «сильного» (динамического) искусственного интеллекта Презентация Сафронов Данила 313 гр
Презентация Сафронов Данила 313 гр Baroque
Baroque Антон Павлович Чехов
Антон Павлович Чехов «Четвертый канал» «Четвертый канал» - это первая независимая негосударственная телекомпания Екатеринбурга. Наша работа отмечена
«Четвертый канал» «Четвертый канал» - это первая независимая негосударственная телекомпания Екатеринбурга. Наша работа отмечена  Международное сотрудничество МГТУ
Международное сотрудничество МГТУ Компьютерные вирусы и защита от них
Компьютерные вирусы и защита от них Интерактив. Вопросы. Мода 19 век
Интерактив. Вопросы. Мода 19 век Стойка на правом (левом) колене
Стойка на правом (левом) колене Технологическое оборудование предприятий общественного питания
Технологическое оборудование предприятий общественного питания Красивая осанка - залог здоровья
Красивая осанка - залог здоровья Правописание О-Ё после шипящих и Ц в корнях, суффиксах всех частей речи
Правописание О-Ё после шипящих и Ц в корнях, суффиксах всех частей речи Утечка умов и национальная безопасность России
Утечка умов и национальная безопасность России Экономика родного края (3 класс)
Экономика родного края (3 класс) История дизайна - часть проектно-художественной деятельности
История дизайна - часть проектно-художественной деятельности Различные аспекты и методы управления организацией
Различные аспекты и методы управления организацией Оперативный и производственный контроль
Оперативный и производственный контроль Лес и его обитатели
Лес и его обитатели www.DEMETA.net www.Atec.de www.Pro2.de
www.DEMETA.net www.Atec.de www.Pro2.de