Содержание
- 2. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ТЕОРИИ ГРАФОВ Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783). Через город протекает
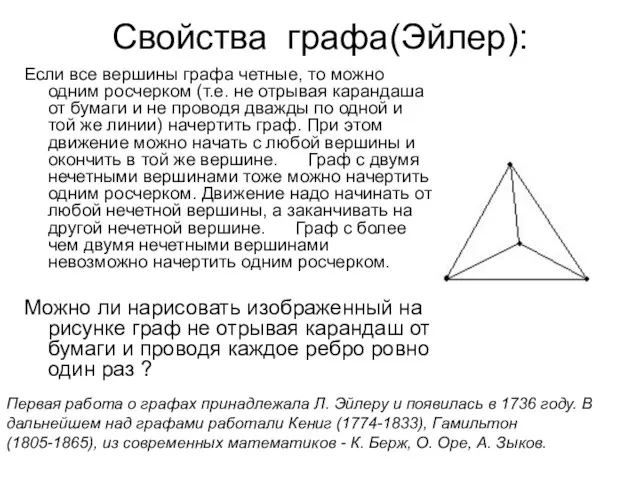
- 3. Свойства графа(Эйлер): Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от
- 4. Задача Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля
- 5. Задача На урок в танцкласс пришли слон, волк и лев. Партнершами для них были выбраны мышка,
- 6. Задача Винни-Пух решил навестить своих друзей: Пятачка, Кролика и Иа-Иа. Ему обязательно нужно побывать у каждого
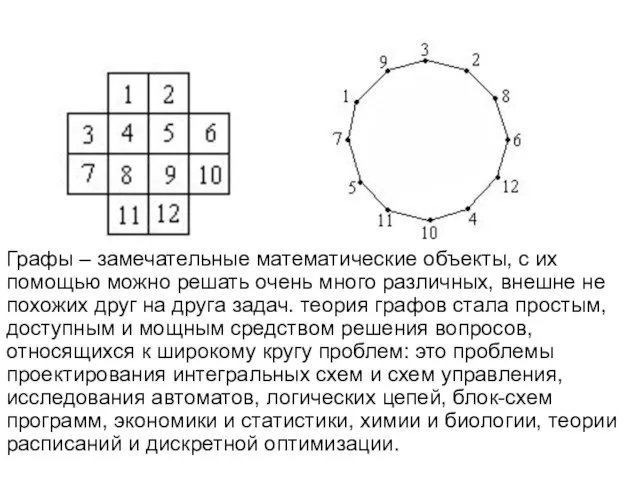
- 7. Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих
- 8. Основные понятия теории графов Граф задается парой множеств G(V,R) Вершины называются смежными, если их соединяет ребро
- 9. Основные понятия теории графов Маршрут графа – последовательность чередующихся вершин и ребер Замкнутый маршрут – маршрут,
- 10. Основные понятия теории графов Ориентированный граф (орграф) имеет направленные ребра – дуги Входящая степень вершины –
- 11. Способы задания графа Явное задание графа как алгебраической системы {a,b,c,d}: {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)} Геометрический Матрица смежности Матрица
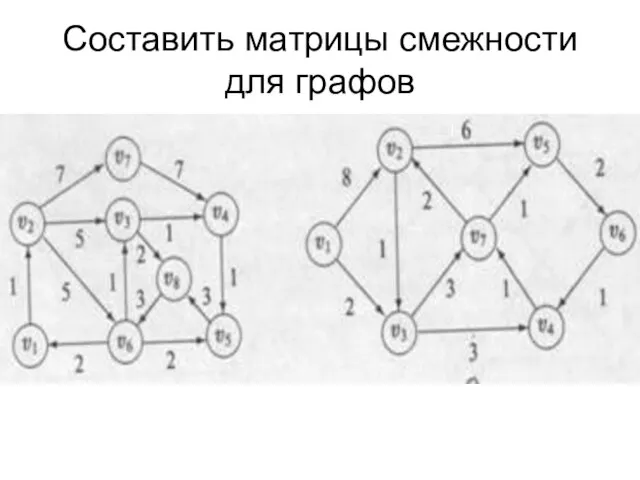
- 12. Составить матрицы смежности для графов
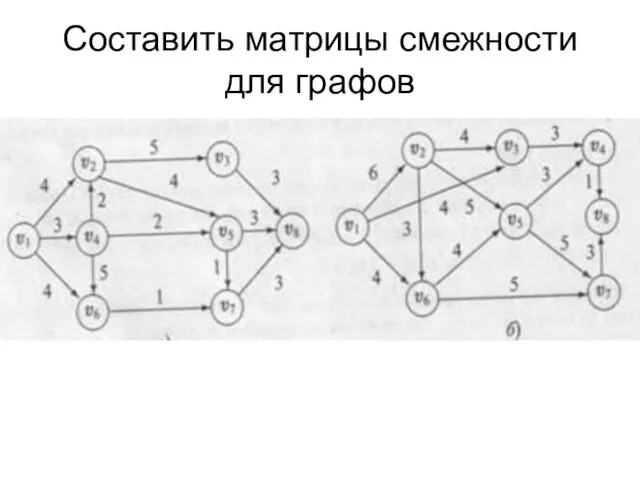
- 13. Составить матрицы смежности для графов
- 14. Основные понятия теории графов(продолжение) Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит
- 15. Основные понятия теории графов Цикломатическое число γ показывает, сколько ребер нужно удалить из графа, чтобы в
- 16. Алгоритм Крускала построения остовного связного дерева минимального веса Построение остовного подграфа с изолированными вершинами Упорядочить ребра
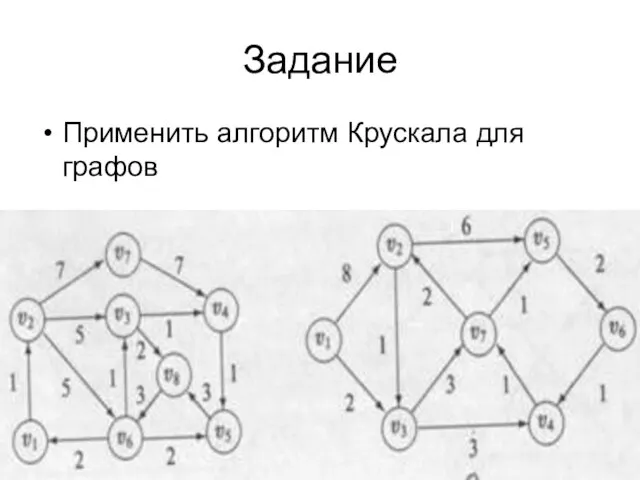
- 17. Задание Применить алгоритм Крускала для графов
- 19. Скачать презентацию











 Организационно-технологическая подготовка к строительству высокоскоростных магистралей
Организационно-технологическая подготовка к строительству высокоскоростных магистралей Художественное воплощение образов Достоевского
Художественное воплощение образов Достоевского Культура Индии
Культура Индии Теория личности. Общение. Стиль общения, качество и культура общения
Теория личности. Общение. Стиль общения, качество и культура общения Бухгалтерский учет. Хозяйственные средства предприятия
Бухгалтерский учет. Хозяйственные средства предприятия Арабские цифры
Арабские цифры «Совершенствование методического сопровождения образовательного процесса в начальной школе на основе опыта реализации современ
«Совершенствование методического сопровождения образовательного процесса в начальной школе на основе опыта реализации современ Расчет фрактальных антенн
Расчет фрактальных антенн Влияние творчества Джона Рональда Руэла Толкина на современную молодежь
Влияние творчества Джона Рональда Руэла Толкина на современную молодежь ОПРОГ1-1
ОПРОГ1-1 Презентация
Презентация Prezentatsia_Microsoft_PowerPoint (3)
Prezentatsia_Microsoft_PowerPoint (3) Новые возможности увеличения дохода РА и повышения лояльности клиентов за счёт использования партнёрских программ
Новые возможности увеличения дохода РА и повышения лояльности клиентов за счёт использования партнёрских программ Аланин
Аланин Новый год и РусЭйр
Новый год и РусЭйр Подготовка педагога к исследовательскому обучению
Подготовка педагога к исследовательскому обучению Эксплуатация рулевого электропривода судна РМС “Капитан Евсеев” ПАО Океанрыбфлот
Эксплуатация рулевого электропривода судна РМС “Капитан Евсеев” ПАО Океанрыбфлот Государства и народы доколумбовой Америки
Государства и народы доколумбовой Америки Информация и цивилизация
Информация и цивилизация Интерьер который мы создаём. 8 класс
Интерьер который мы создаём. 8 класс Исследовательская работа ученицы 3 класса МОУ СОШ №1 ЛОРАЙ ЕЛЕНЫ на тему «ВЫРАЩИВАНИЕ МОЖЖЕВЕЛЬНИКА В УСЛОВИЯХ ТУЛЬСКОЙ
Исследовательская работа ученицы 3 класса МОУ СОШ №1 ЛОРАЙ ЕЛЕНЫ на тему «ВЫРАЩИВАНИЕ МОЖЖЕВЕЛЬНИКА В УСЛОВИЯХ ТУЛЬСКОЙ  Презентация на тему ОБЩАЯ И ОСОБЕННАЯ ЧАСТИ ГРАЖДАНСКОГО ПРАВА
Презентация на тему ОБЩАЯ И ОСОБЕННАЯ ЧАСТИ ГРАЖДАНСКОГО ПРАВА  Новоиерусалимский монастырь
Новоиерусалимский монастырь Как прекрасен этот мир
Как прекрасен этот мир Права и свободы человека и гражданина
Права и свободы человека и гражданина Профилактика артрита
Профилактика артрита Презентация на тему Декабристы. Первые русские революционеры (10 класс)
Презентация на тему Декабристы. Первые русские революционеры (10 класс) Результаты участия выпускников школы «Премьер» в независимых тестированиях (ЕГЭ; ГИА)
Результаты участия выпускников школы «Премьер» в независимых тестированиях (ЕГЭ; ГИА)