Графы и их применение (11 класс)

Графы и
их применение

Выяснить особенности применения теории графов при решении задач и в практической деятельности.
Цель:

- изучить теорию графов;
- решить задачи с помощью графов;
- рассмотреть применение теории графов в различных областях науки;
- разработать оптимальный вариант ремонта кухни с помощью сетевого графика;
- составить генеалогическое древо.
Задачи:

Родоначальником теории графов принято считать математика Леонарда Эйлера(1707-1783). Он предложил изящное решение знаменитой задачи о 7 Кенигсбергских мостах в 1736 году, а также придумал общий метод решения подобных задач.
Из истории графов

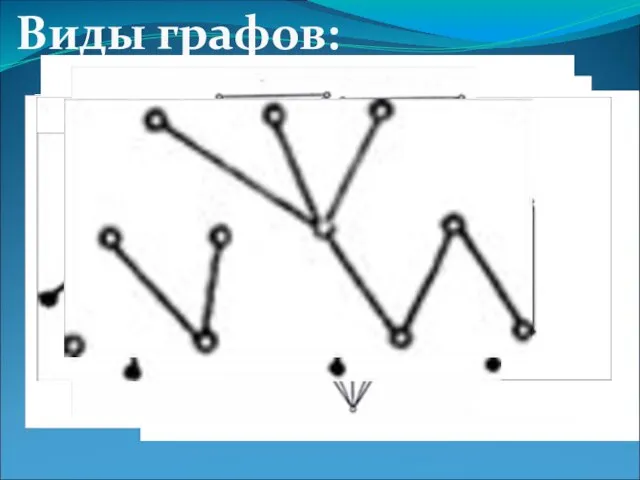
Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.
Теория графов - раздел математики, особенность которого геометрический подход к изучению объектов.
Теория графов

1) Нулевой граф
2) Неполный граф
3) Полный граф
4) Несвязный граф
5) Связный граф
6) Ориентированный граф (орграф)
7) Взвешенный граф
8) Эйлеровый граф
9) Плоский граф
10) Дерево
11) Лес
Виды графов:

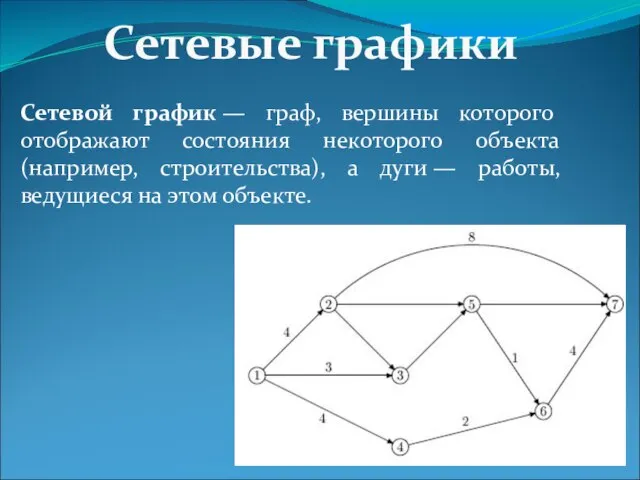
Сетевой график — граф, вершины которого отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте.
Сетевые графики

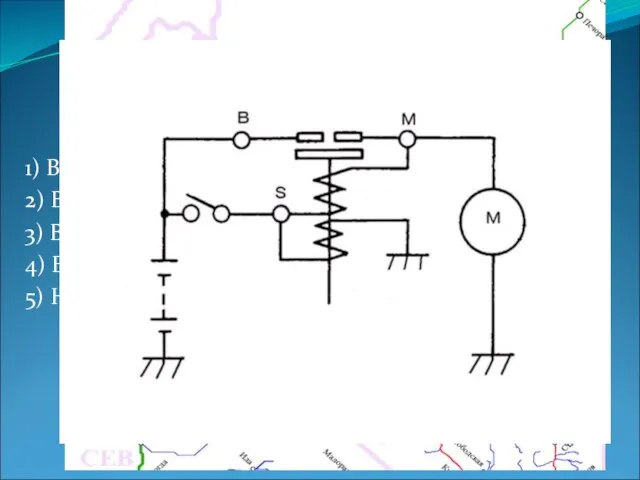
1) В теории информации
2) В биологии
3) В химии
4) В физике
5) На транспорте
Применение
теории графов:

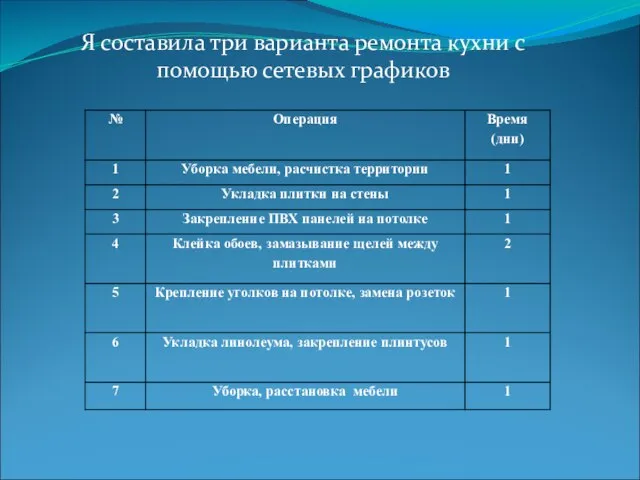
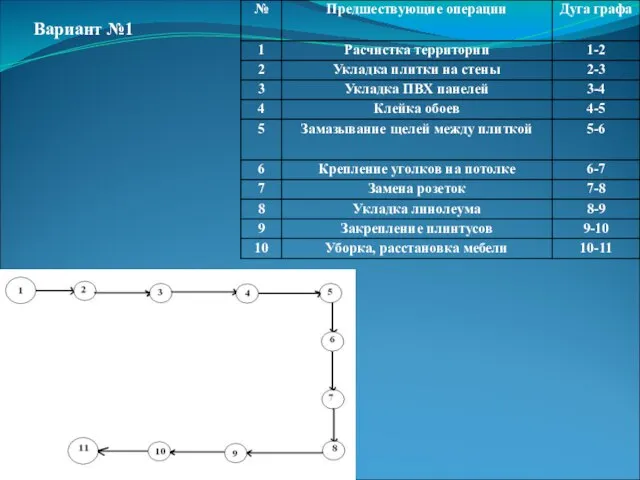
Я составила три варианта ремонта кухни с помощью сетевых графиков

Вариант №1

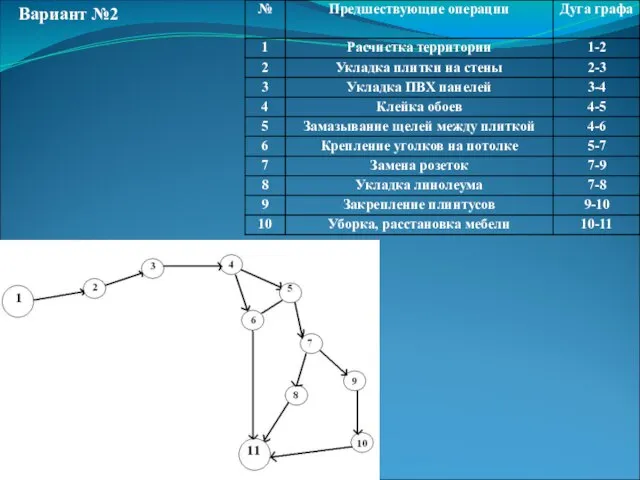
Вариант №2

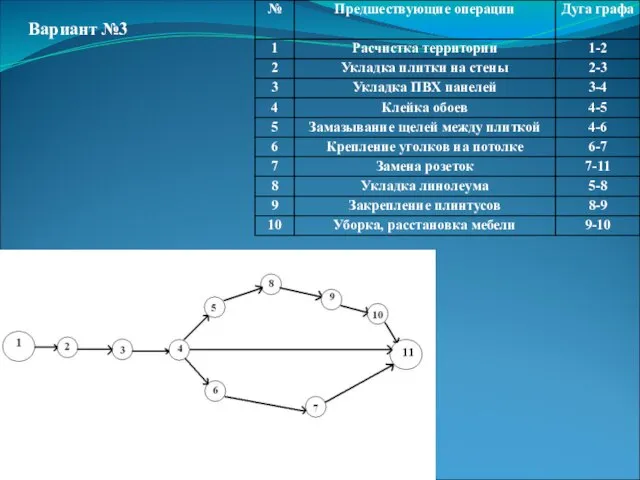
Вариант №3

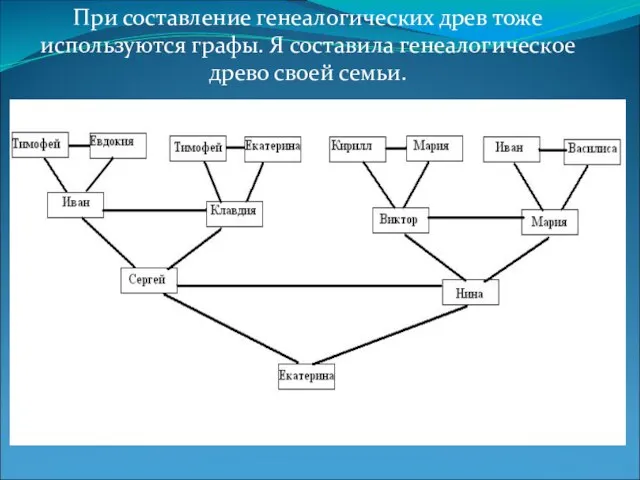
При составление генеалогических древ тоже используются графы. Я составила генеалогическое древо своей семьи.

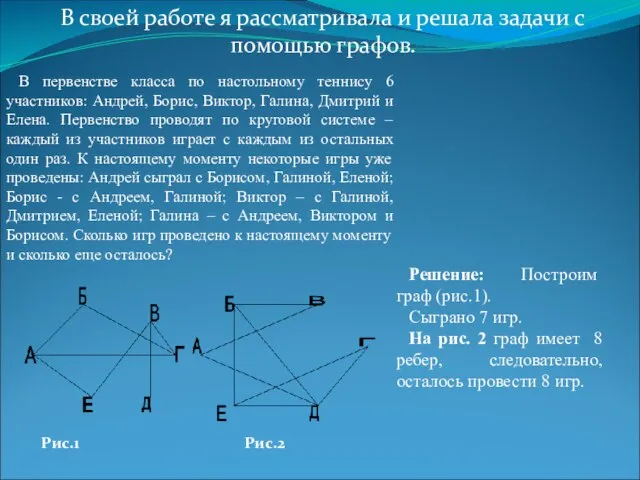
В своей работе я рассматривала и решала задачи с помощью графов.
В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис - с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?
Рис.1 Рис.2
Решение: Построим граф (рис.1).
Сыграно 7 игр.
На рис. 2 граф имеет 8 ребер, следовательно, осталось провести 8 игр.

Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?
10 рукопожатий

Из цифр 9, 7, 5, 0 составляют все возможные трехзначные числа, в которых нет одинаковых цифр. Сколько среди чисел, меньше 900?

Графы представляют изучаемые факты в наглядной форме. Решение многих математических задач упрощается, если удается использовать графы. Графовые задачи позволяют развивать воображение и логическое мышление.
Теория графов в настоящее время является интенсивно развивающимся разделом математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношения между людьми и многое другое.
Заключение