Содержание
- 2. Далеко-далеко. Куда не летают даже самолёты, находится страна Геометрия. В этой необычной стране был удивительный город-город
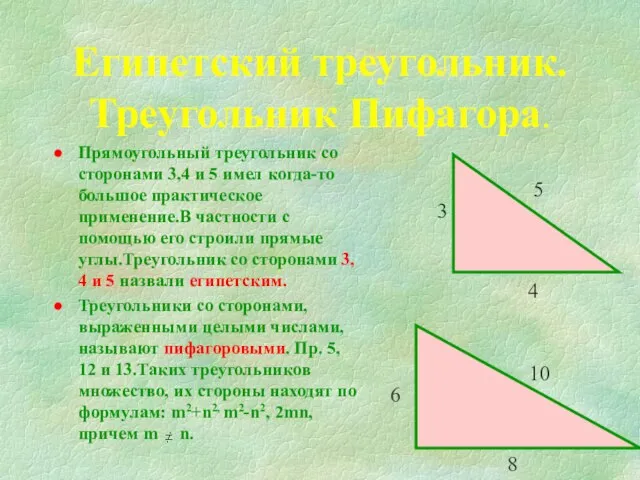
- 3. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Теорема Пифагора а b c гипотенуза катет
- 4. Египетский треугольник. Треугольник Пифагора. Прямоугольный треугольник со сторонами 3,4 и 5 имел когда-то большое практическое применение.В
- 5. Пифагоровы числа или пифагоровы тройки. Это великое открытие пифагорейских математиков. Тройки чисел таких, что a2+b2=c2. Интересные
- 7. Предисловие. Еще давно была изобретена головоломка, называемая сегодня “Пифагор”. Нетрудно убедиться в том, что в основе
- 8. Первое доказательство. (алгебраическое) Пусть Т—прямоугольный треугольник с катетами а, b и гипотенузой с(рис. 6, а). Докажем,
- 9. Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого
- 10. Не алгебраические доказательства теоремы. Простейшее доказательство. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных
- 11. Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том,
- 12. Древнекитайское доказательство. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b
- 13. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В
- 14. Доказательство Евклида приведено в предложении 47 первой книги “Начал”. На гипотенузе и катетах прямоугольного треугольника АВС
- 15. О доказательстве Евклида Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой
- 17. Скачать презентацию
Слайд 2 Далеко-далеко. Куда не летают даже самолёты, находится страна Геометрия.
В этой
Далеко-далеко. Куда не летают даже самолёты, находится страна Геометрия.
В этой

Введение
Сказка «Дом»
Слайд 3В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема Пифагора
а
b
c
гипотенуза
катет
катет
Теорема Пифагора
а
b
c
гипотенуза
катет
катет
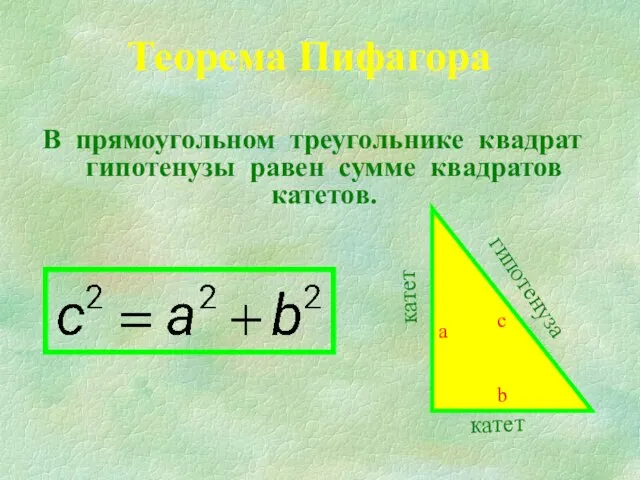
Слайд 4Египетский треугольник.
Треугольник Пифагора.
Прямоугольный треугольник со сторонами 3,4 и 5 имел когда-то
Египетский треугольник.
Треугольник Пифагора.
Прямоугольный треугольник со сторонами 3,4 и 5 имел когда-то
Треугольники со сторонами, выраженными целыми числами, называют пифагоровыми. Пр. 5, 12 и 13.Таких треугольников множество, их стороны находят по формулам: m2+n2, m2-n2, 2mn, причем m n.
3
4
5
6
8
10
Слайд 5Пифагоровы числа или пифагоровы тройки. Это великое открытие пифагорейских математиков.
Тройки чисел
Пифагоровы числа или пифагоровы тройки. Это великое открытие пифагорейских математиков.
Тройки чисел

Интересные особенности этих чисел:
Один из «катетов» должен быть кратным трём.
Один из «катетов» должен быть кратным четырём.
Одно из Пифагоровых чисел должно быть кратно пяти.
«Пифагоровы тройки»
Слайд 7Предисловие.
Еще давно была изобретена головоломка, называемая сегодня “Пифагор”. Нетрудно убедиться в
Предисловие.
Еще давно была изобретена головоломка, называемая сегодня “Пифагор”. Нетрудно убедиться в

Алгебраические доказательства теоремы
Слайд 8Первое доказательство. (алгебраическое)
Пусть Т—прямоугольный треугольник с катетами а, b и гипотенузой
Первое доказательство. (алгебраическое)
Пусть Т—прямоугольный треугольник с катетами а, b и гипотенузой

Докажем, что с2=а2+Ь2.
Построим квадрат Q со стороной а+Ь (рис. 6, б). На сторонах квадрата Q возьмем точки А, В, С, D
так, чтобы отрезки АВ, ВС, CD, DA отсекали от квадрата Q прямоугольные треугольники Т1, Т2, Т3, Т4
с катетами а и b. Четырехугольник ABCD обозначим буквой Р. Покажем, что Р — квадрат со
стороной с.
Все треугольники Т1, Т2, Т3, Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны
гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые.
Пусть α и β— величины острых углов треугольника Т. Тогда, как вам известно, α+β= 90°. Угол у при
вершине А четырехугольника Р вместе с углами, равными α и β, составляет развернутый угол.
Поэтому α+β=180°. И так как α+β= 90°, то γ=90°. Точно так же доказывается, что и остальные углы
четырехугольника Р прямые. Следовательно, четырехугольник Р — квадрат со стороной с.
Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных
треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T) .
Так как S(Q)=(a+b) 2 ; S(P)=c2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4S(T),
получаем равенство (a+b) 2=c2+4*(1/2)ab .
Поскольку (a+b)2=a2+b2+2ab, то равенство
(a+b)2=c2+4*(1/2)ab
можно записать так: a2+b2+2ab=c2+2ab.
Из равенства a2+b2+2ab=c2+2ab следует,
что с2=а2+Ь2. Ч.Т.Д.
Слайд 9Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту
Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту
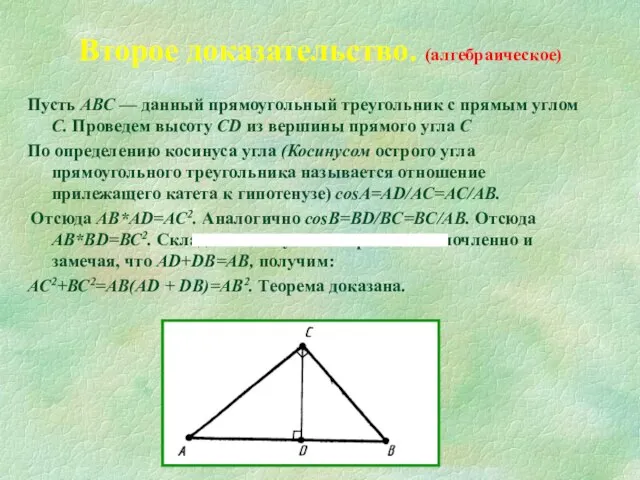
По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB.
Отсюда AB*AD=AC2. Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2. Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим:
АС2+ВС2=АВ(AD + DB)=АВ2. Теорема доказана.
Второе доказательство. (алгебраическое)
Слайд 10
Не алгебраические доказательства теоремы.
Простейшее доказательство.
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик
Не алгебраические доказательства теоремы.
Простейшее доказательство.
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например,
для ∧ABC : квадрат, построенный на гипотенузе АС,
содержит 4 исходных треугольника, а квадраты,
построенные на катетах,— по два.
Теорема доказана.
Рис.1
Слайд 11Математические трактаты Древнего Китая дошли до нас в редакции II в. до
Математические трактаты Древнего Китая дошли до нас в редакции II в. до

Древнекитайское доказательство.
(не алгебраическое)
Предисловие.
Слайд 12Древнекитайское доказательство.
В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника
Древнекитайское доказательство.
В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника
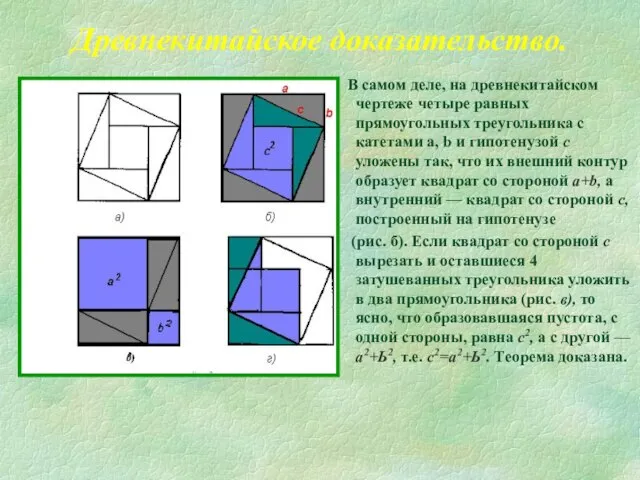
(рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана.
Слайд 13 Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать
Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать

a и b (рис.1и2).После чего писали одно слово “Смотри!”. И действительно, взглянув на эти рисунки, видим, что слева свободна от треугольников фигура, состоящая из двух квадратов со сторонами a и b,соответственно её площадь равна a²+b², а справа- квадрат со стороной c -его площадь равна c² . Значит, a²+b²=c², что и составляет утверждение теоремы Пифагора.
чертеж из трактата
“Чжоу-би...”.
рис.1
рис.2
Древнеиндийское доказательство.
Слайд 14 Доказательство Евклида приведено в предложении 47 первой книги “Начал”. На гипотенузе
Доказательство Евклида приведено в предложении 47 первой книги “Начал”. На гипотенузе

используя равенство треугольников ВСК и АСЕ,доказывается, что SJCEL=SACKG. Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED ,
что и требовалось доказать.
Доказательство Евклида.
Слайд 15О доказательстве Евклида
Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно
О доказательстве Евклида
Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно

Еще давно была изобретена головоломка, называемая сегодня “Пифагор”. Нетрудно убедиться в том, что в основе семи частей головоломки лежат равнобедренный прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат. Такова лишь малая толика богатств, скрытых в жемчужине античной математики — теореме Пифагора.

 Презентация на тему Аппликация из ткани
Презентация на тему Аппликация из ткани План этажа
План этажа современные решения для автобизнеса
современные решения для автобизнеса День открытых дверей. Приемная кампания на 2021-2022 учебный год
День открытых дверей. Приемная кампания на 2021-2022 учебный год Размножение и развитие птиц. Годовой жизненный цикл. Сезонные явления
Размножение и развитие птиц. Годовой жизненный цикл. Сезонные явления «Оптимизация межкультурного взаимодействия как стратегическое условие противодействия ксенофобии и этнокультурному экстремизм
«Оптимизация межкультурного взаимодействия как стратегическое условие противодействия ксенофобии и этнокультурному экстремизм Игра – путешествие по сказкам А.С.Пушкина
Игра – путешествие по сказкам А.С.Пушкина Интеграция ДО в единую информационную среду Лицея
Интеграция ДО в единую информационную среду Лицея Вибрационные методы диагностики
Вибрационные методы диагностики Всемирный день моря
Всемирный день моря Атомно-абсорбционный анализ
Атомно-абсорбционный анализ Цель проекта: 1.Показать, что понимание человечеством функциональных связей и взаимосвязей между отдельными качествами жизни(добр
Цель проекта: 1.Показать, что понимание человечеством функциональных связей и взаимосвязей между отдельными качествами жизни(добр Видеопрезентация учителя французского языка Тутаевой Елены Николаевны
Видеопрезентация учителя французского языка Тутаевой Елены Николаевны Презентация на тему Склонение имен существительных
Презентация на тему Склонение имен существительных  Публичный информационно-аналитический доклад о состоянии и результатах деятельности муниципального общеобразовательного уч
Публичный информационно-аналитический доклад о состоянии и результатах деятельности муниципального общеобразовательного уч Портрет в русской живописи начала ХІХ века
Портрет в русской живописи начала ХІХ века Кинотеатр имени А.С. Пушкина
Кинотеатр имени А.С. Пушкина Антимонопольный контроль на рынке автомобильного топлива
Антимонопольный контроль на рынке автомобильного топлива План проведения недели математики
План проведения недели математики Загадки трудных слов
Загадки трудных слов  Святки
Святки MEDICAL SYMBOLS: FACTS, ERRORS AND CONFUSION Moreover
MEDICAL SYMBOLS: FACTS, ERRORS AND CONFUSION Moreover Презентация на тему Мультимедиа технологии
Презентация на тему Мультимедиа технологии  Презентация на тему Презентация к уроку окружающего мира 4 класс
Презентация на тему Презентация к уроку окружающего мира 4 класс  Батырлык дәресе “Кайнар йөрәк”
Батырлык дәресе “Кайнар йөрәк” Корпоративная культура
Корпоративная культура Высшая школа менеджмента Санкт-Петербургский государственный университет Библиотека современной школы бизнеса: формирование к
Высшая школа менеджмента Санкт-Петербургский государственный университет Библиотека современной школы бизнеса: формирование к Программа Непрерывного ОбразованияGRUNDTVIG Многосторонний проект INTEGRA- Объединение Мигрантов - Элементарные Языкоые знания для Ко
Программа Непрерывного ОбразованияGRUNDTVIG Многосторонний проект INTEGRA- Объединение Мигрантов - Элементарные Языкоые знания для Ко