I. СИСТЕМЫ СЧИСЛЕНИЯ

Система счисления -
это способ записи чисел.
64, \/

Системы счисления
Позиционные Непозиционные

Позиционные-
Позиционные системы счисления - системы записи чисел, в которых значение каждой цифры числа зависит от ее положения (позиции) в последовательности цифр.
Примеры: двоичная(101101),
десятичная(123, 15).

Непозиционные -
каждой цифре соответствует величина, не зависящая от её места в записи числа
Пример: римская( XXI, IV)

Десятичная
Система счисления с основанием 10.
Возникла примерно в V веке нашей эры в Индии.

Двоичная
Позиционная система счисления с основанием два.

II. Перевод чисел из одной СС в другую.

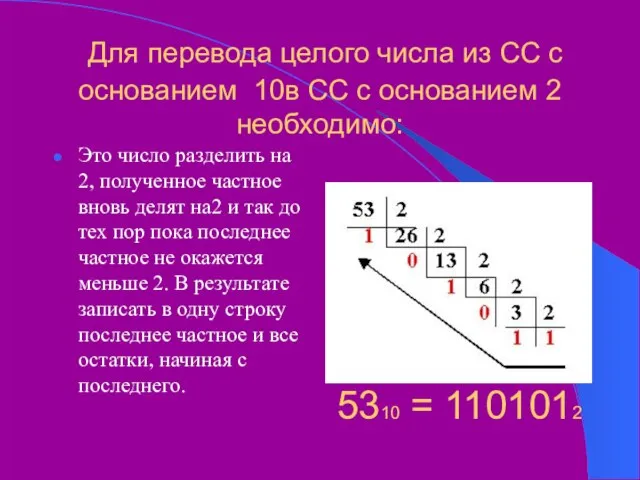
Для перевода целого числа из СС с основанием 10в СС с основанием 2 необходимо:
Это число разделить на 2, полученное частное вновь делят на2 и так до тех пор пока последнее частное не окажется меньше 2. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
5310 = 1101012

Для перевода правильной дроби из СС с основанием 10 в СС с основанием 2 необходимо:
эту дробь умножить на 2, затем дробную часть, полученного произведения вновь умножить на 2 и так до тех пор пока в дробной части не окажутся все нули, либо не будет достигнута заданная степень точности. Целые части, полученных произведений взятые по схеме сверху вниз, и дадут результат перевода.
0,2510 = 0,012

Для перевода смешанной дроби из одной СС в другую необходимо:
представить эту дробь в виде суммы целого числа и десятичной дроби, а затем произвести перевод каждой части отдельно по соответствующим правилам.

Перевести 25,2510 в двоичную СС
Рассмотрим пример:

Сначала- переводим целую часть
2510=110012

Затем- перевод дробной части
0,2510=0,012

Соединили целую и дробную части и получили:
25,250010=11001,012
целая часть
дробная часть