промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?
1) 70 бит 2) 70 байт 3) 490 бит 4) 119 байт
Решение:
Для решения необходимо воспользоваться формулой нахождения количества информации Хартли, так как события «прохождение» или «не прохождение» для участников велокросса равновероятностные:
I = log2 K, К - количество равновероятных событий;
I - количество бит в сообщении, такое, что любое из К событий произошло. Тогда K = 2I. В нашем случае К – это количество участников, а I - это минимальное количество бит, необходимых для того чтобы любое из К событий произошло.
K = 119, 119 = 2I Если I = 7 → 27 = 128, и этого количества бит достаточно для регистрации прохождения 119-ти спортсменов. 7 бит – минимальное количество бит.
Всего прошло 70 спортсменов, значит информационный объем сообщения равен:
70 * 7 = 490 бит.
Правильный ответ – 3.













 Решение уравнений
Решение уравнений Грузовое устройство
Грузовое устройство Катаргина Наталья Юрьевна.
Катаргина Наталья Юрьевна. Новогоднее представление Мышеловка для Деда Мороза
Новогоднее представление Мышеловка для Деда Мороза Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация
Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация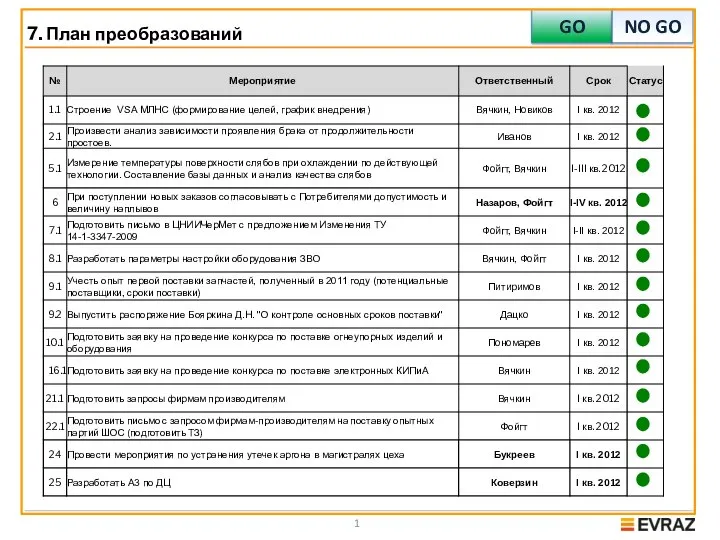 План преобразований. Отслеживание результатов
План преобразований. Отслеживание результатов Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка
Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка  Поводы и основания к возбуждению уголовного дела
Поводы и основания к возбуждению уголовного дела Вольфганг Амадей Моцарт
Вольфганг Амадей Моцарт Съемки подземных сооружений и коммуникаций
Съемки подземных сооружений и коммуникаций Проблема истинной человечности в рассказе К. Паустовского “Телеграмма”
Проблема истинной человечности в рассказе К. Паустовского “Телеграмма” Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных
Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных Оценка рисков при проведении форвардных сделок
Оценка рисков при проведении форвардных сделок Управления их классификация
Управления их классификация Стратегия бизнес - проекта «Магазин без очередей и касс»
Стратегия бизнес - проекта «Магазин без очередей и касс» Город и транспорт
Город и транспорт Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное
Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное Презентация на тему Ирак
Презентация на тему Ирак Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году
Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году Ремонт электролизёров на месте установки
Ремонт электролизёров на месте установки Презентация на тему Японское море
Презентация на тему Японское море Ранний железный век в Казахстане
Ранний железный век в Казахстане Passato Reg
Passato Reg Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , «
Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , « Этические и правовые нормы информационной деятельности человека
Этические и правовые нормы информационной деятельности человека Лекция 5 Модель классов предметной области (1)
Лекция 5 Модель классов предметной области (1) Осторожно - мошенники
Осторожно - мошенники Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму
Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму