Содержание
- 2. Goals of this course To provide f thorough and systematic treatment of conceptual and logical design
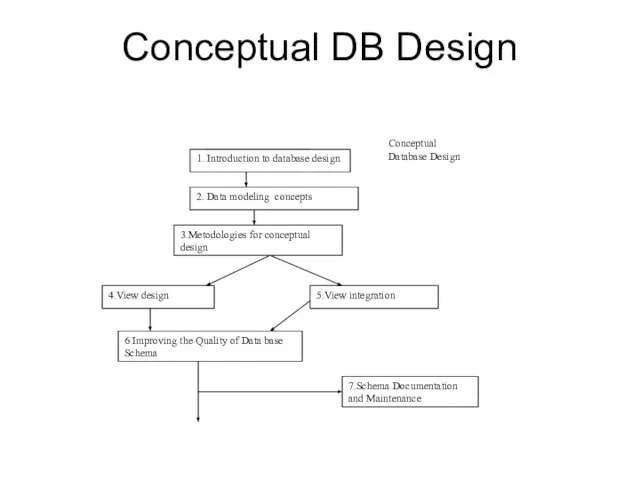
- 3. Conceptual DB Design
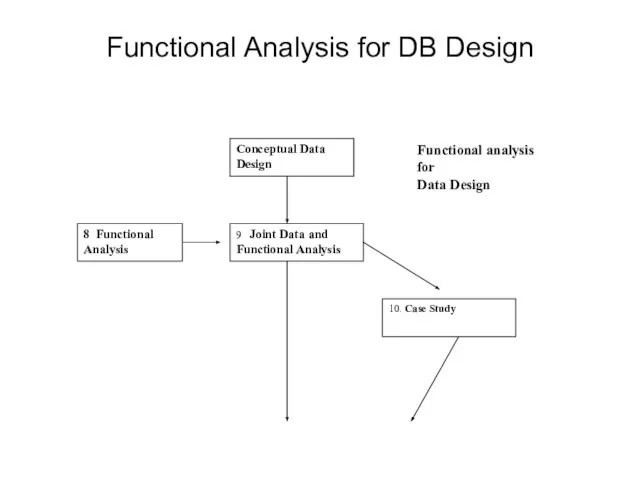
- 4. Functional Analysis for DB Design
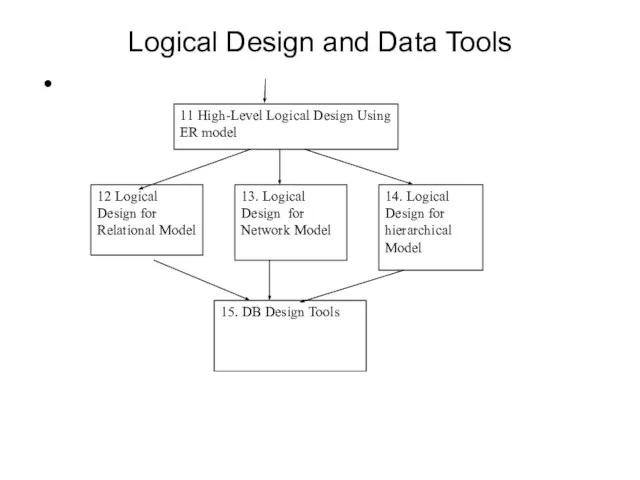
- 5. Logical Design and Data Tools 11 High-Level Logical Design Using ER model 12 Logical Design for
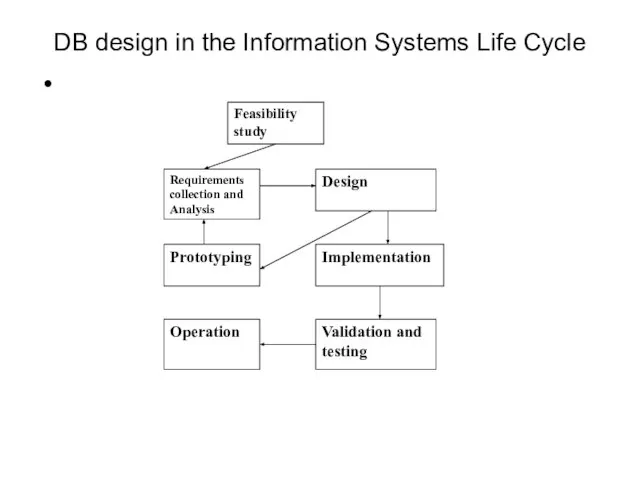
- 6. DB design in the Information Systems Life Cycle
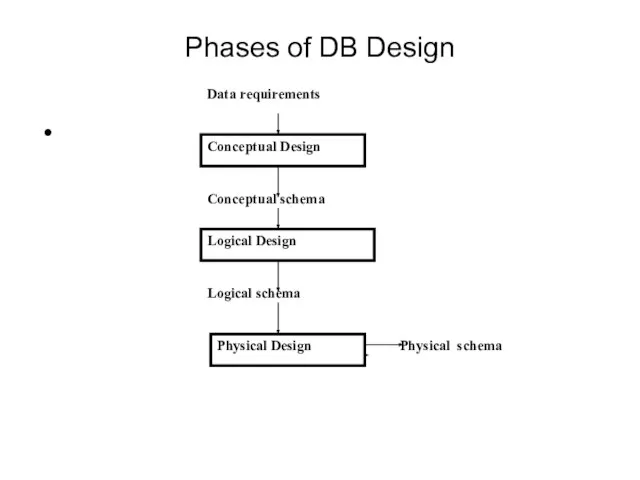
- 7. Phases of DB Design
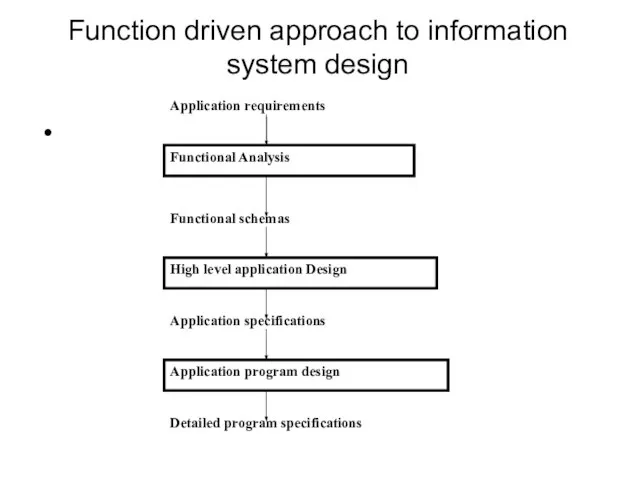
- 8. Function driven approach to information system design
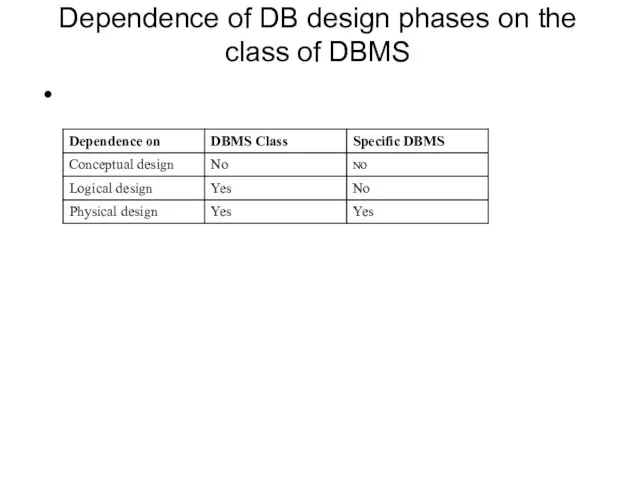
- 9. Dependence of DB design phases on the class of DBMS
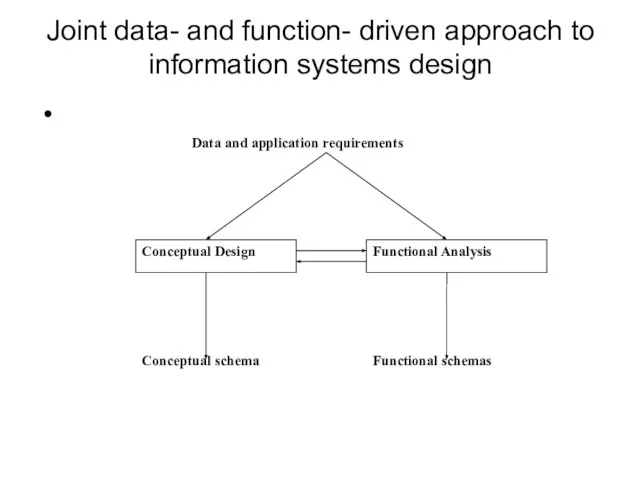
- 10. Joint data- and function- driven approach to information systems design
- 11. Bibliography 1. W.Davis System Analysis and Design : A structured Approach . Addison-Wesley 1983 2. R.Farley
- 12. Data Modeling Concepts
- 13. Structure of the lecture Section 1- Abstractions Section 2- Properties of mapping Section 3- Data models,
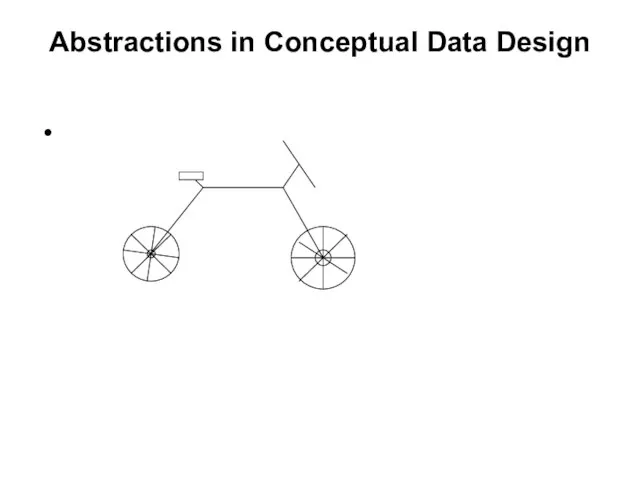
- 14. Abstractions in Conceptual Data Design
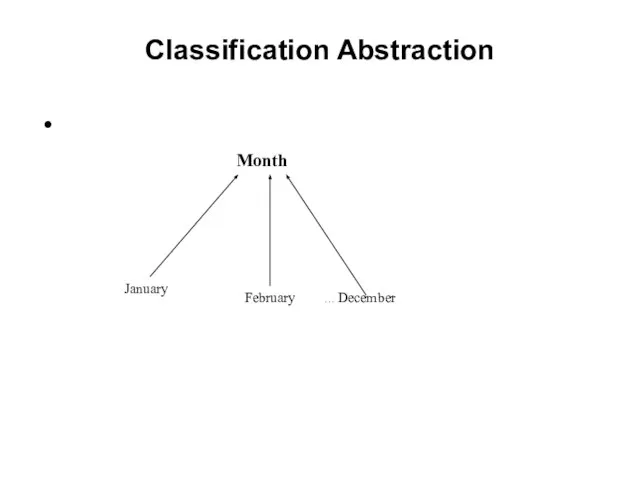
- 15. Classification Abstraction
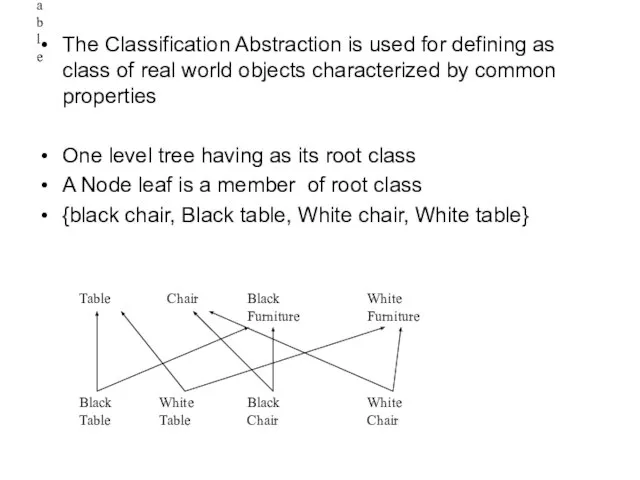
- 16. Table The Classification Abstraction is used for defining as class of real world objects characterized by
- 17. Aggregation Abstraction Aggregation abstraction defines a new class from set of (other) classes that representits component
- 18. Generalization Abstraction A generalization abstraction defines a subset relationship between the elements of two or more
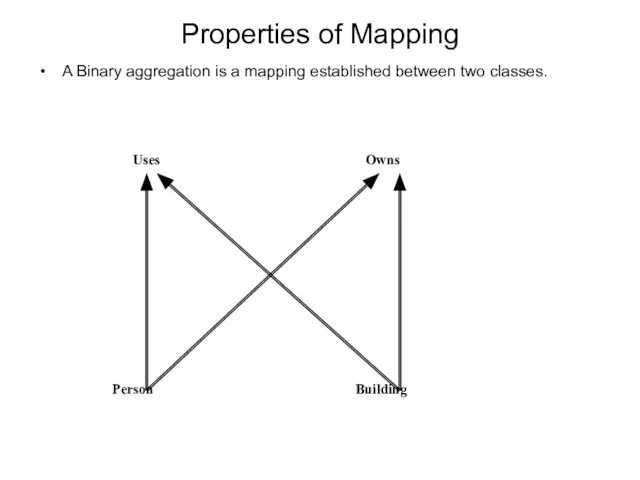
- 19. Properties of Mapping A Binary aggregation is a mapping established between two classes.
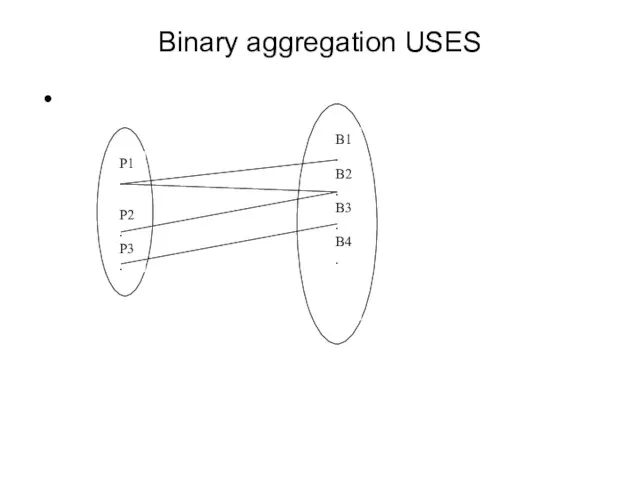
- 20. Binary aggregation USES
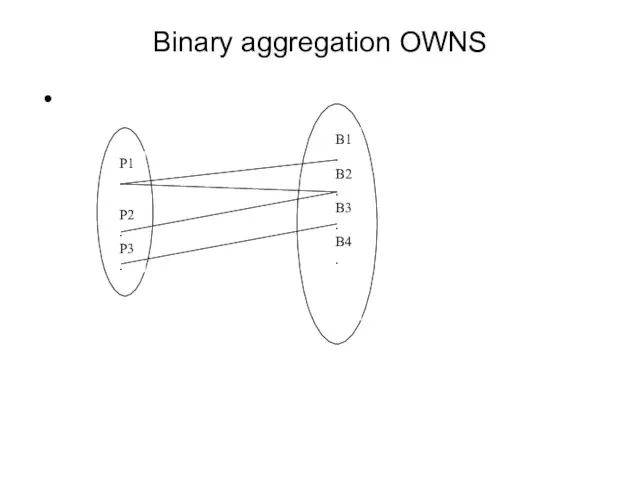
- 21. Binary aggregation OWNS
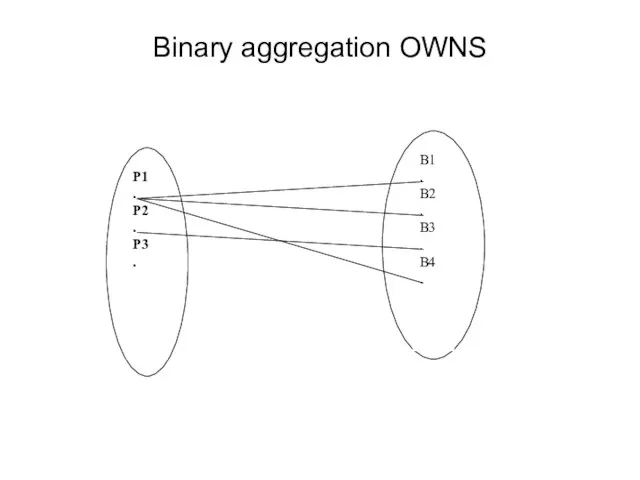
- 22. Binary aggregation OWNS
- 23. Minimal cardinality (min-card) Let us consider aggregation A between classes C1 and C2 The minimal cardinality
- 24. Maximal Cardinality Let us consider aggregation A between classes C1 and C2 The maximal cardinality or
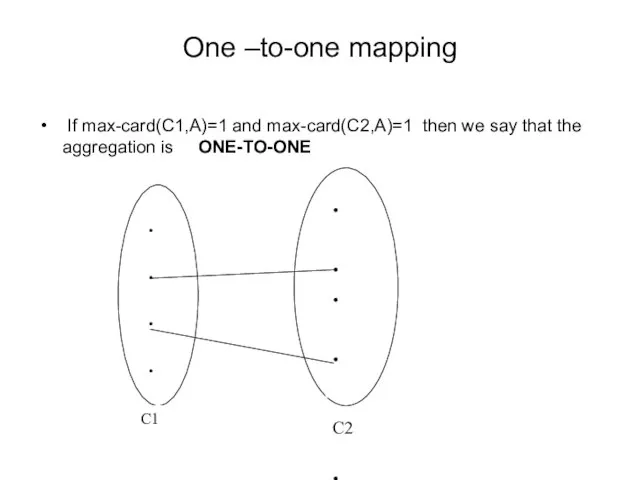
- 25. One –to-one mapping If max-card(C1,A)=1 and max-card(C2,A)=1 then we say that the aggregation is ONE-TO-ONE
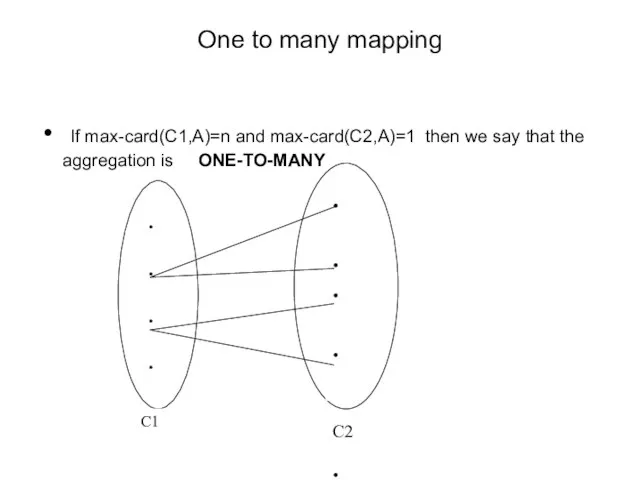
- 26. One to many mapping If max-card(C1,A)=n and max-card(C2,A)=1 then we say that the aggregation is ONE-TO-MANY
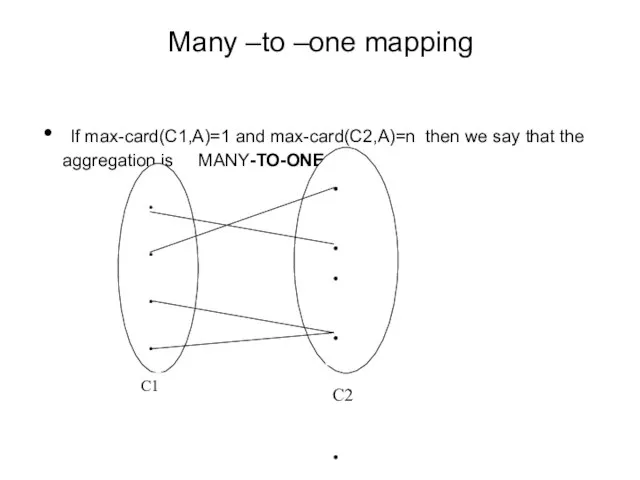
- 27. Many –to –one mapping If max-card(C1,A)=1 and max-card(C2,A)=n then we say that the aggregation is MANY-TO-ONE
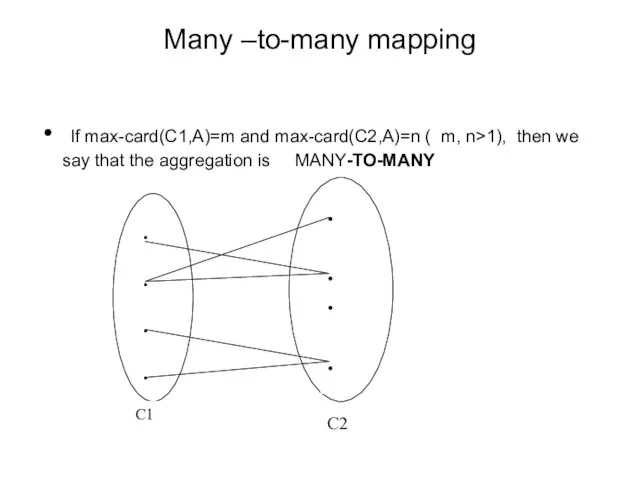
- 28. Many –to-many mapping If max-card(C1,A)=m and max-card(C2,A)=n ( m, n>1), then we say that the aggregation
- 29. N-ary aggregation An n-ary aggregation is a mapping established among three or more classes Minimal Cardinality
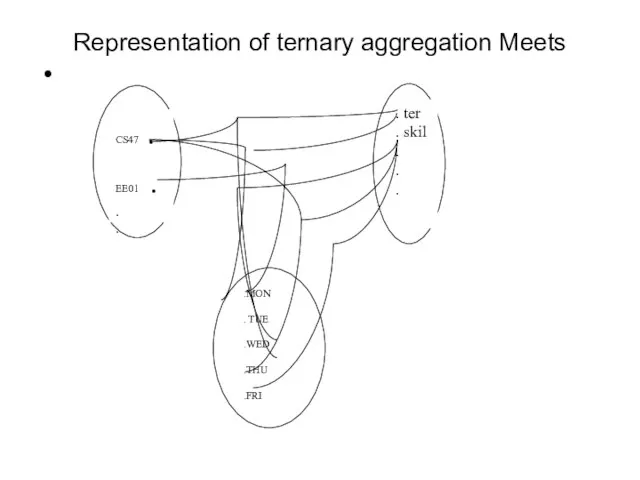
- 30. Representation of ternary aggregation Meets CS47 . EE01 . . . . ter . skil .
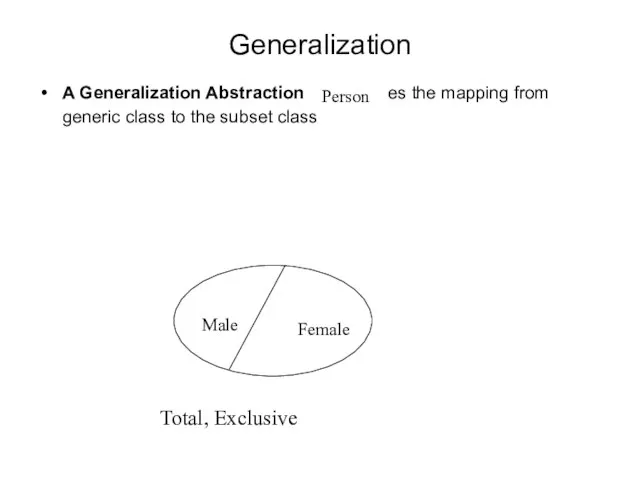
- 31. Generalization A Generalization Abstraction establishes the mapping from generic class to the subset class Person Male
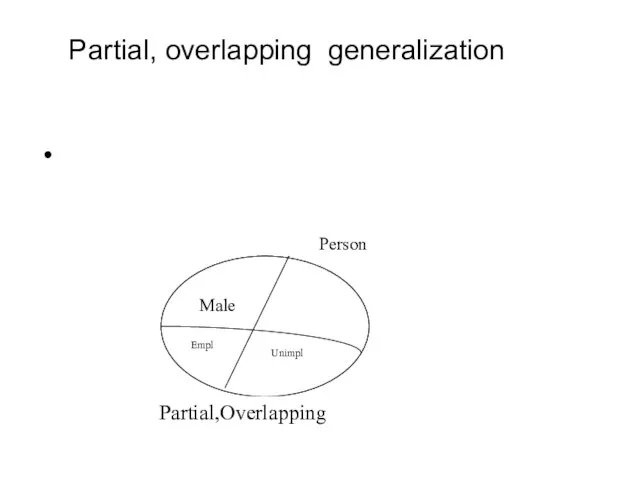
- 32. Partial, overlapping generalization
- 33. Partial, Exclusive Generalization
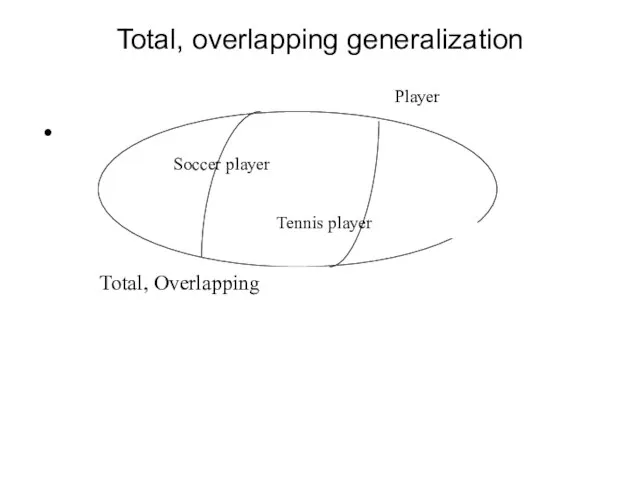
- 34. Total, overlapping generalization
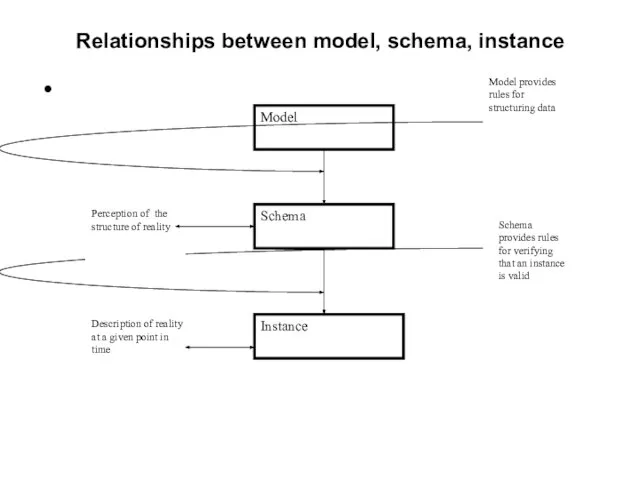
- 35. Data models A Data model is a collection of concepts that can be used to describe
- 36. Schema Schema is a representation of a specific portion of reality, built using a particular data
- 37. Instances An instance of schema is a dynamic, time variant collection of data that conforms to
- 38. Relationships between model, schema, instance
- 39. Qualities of Conceptual Models 1. Expressiveness 2. Simplicity 3. Minimality 4. Formality PROPERTIES OF GRAPHIC REPRESENTATIONS
- 40. The Entity –Relationship Model Basic elements of the ER Model Entities. Entities represent classes of real
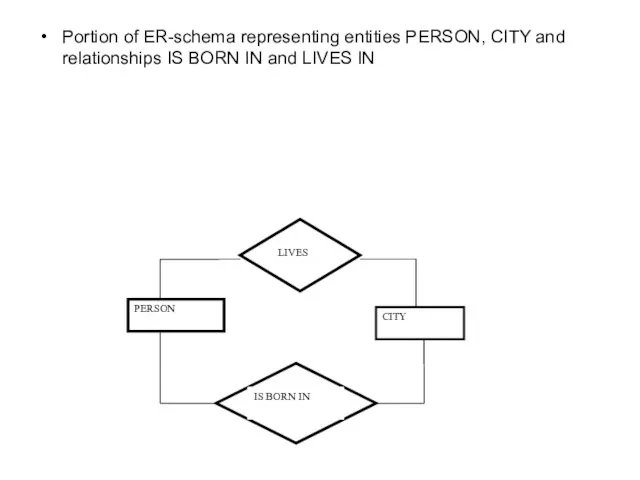
- 41. Portion of ER-schema representing entities PERSON, CITY and relationships IS BORN IN and LIVES IN
- 42. Instance for previous schema PERSON={p1,p2,p3} CITY= {c1,c2,c3} LIVES IN= { , , } IS BORN IN=
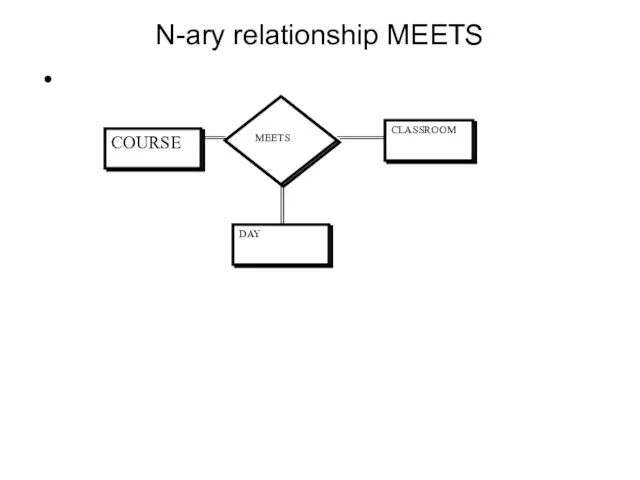
- 43. N-ary relationship MEETS
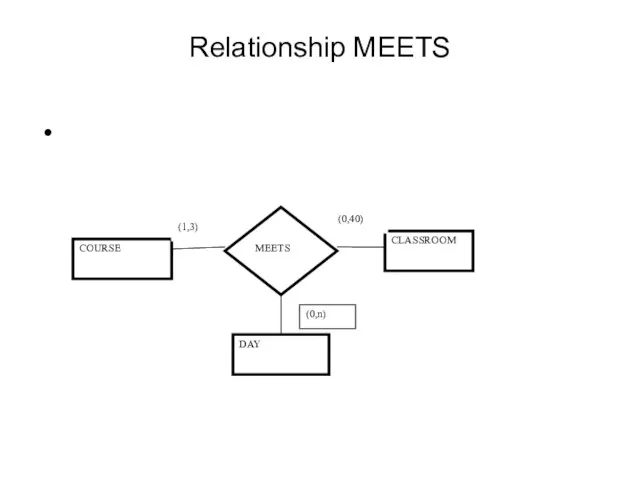
- 44. Relationship MEETS
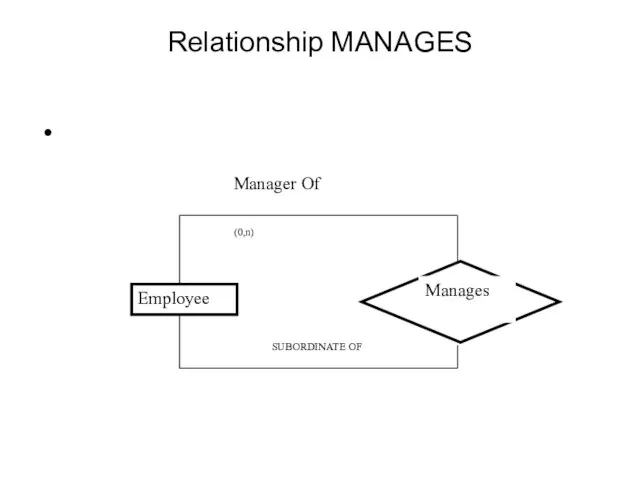
- 45. Relationship MANAGES
- 46. min-card( PERSON,LIVES IN)=1 max-card( PERSON,LIVES IN)=1 min-card( CITY,LIVES IN)=0 max-card( CITY,LIVES IN)=n
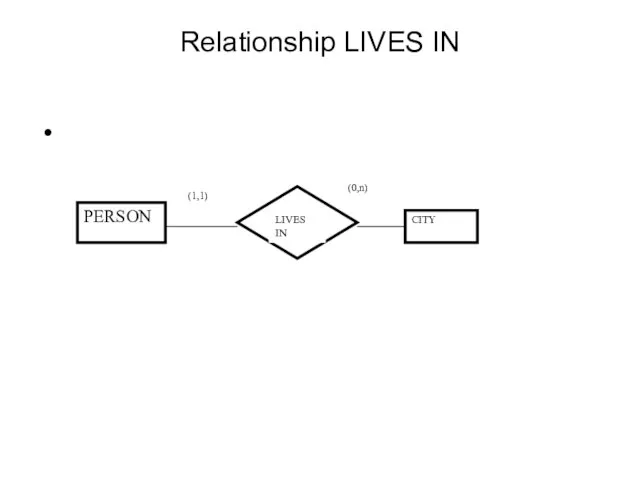
- 47. Relationship LIVES IN
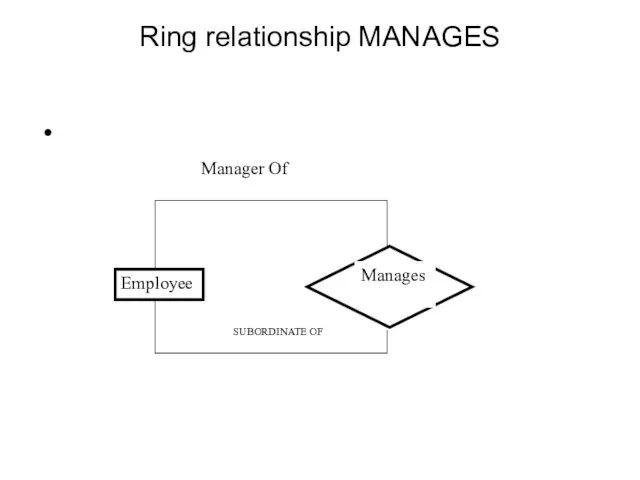
- 48. Ring relationship MANAGES
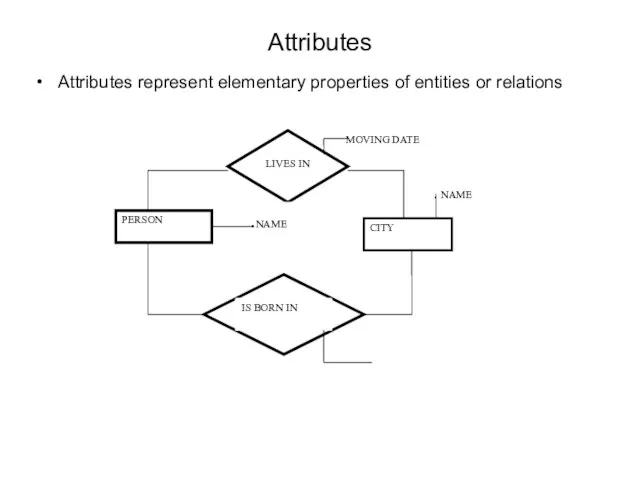
- 49. Attributes Attributes represent elementary properties of entities or relations
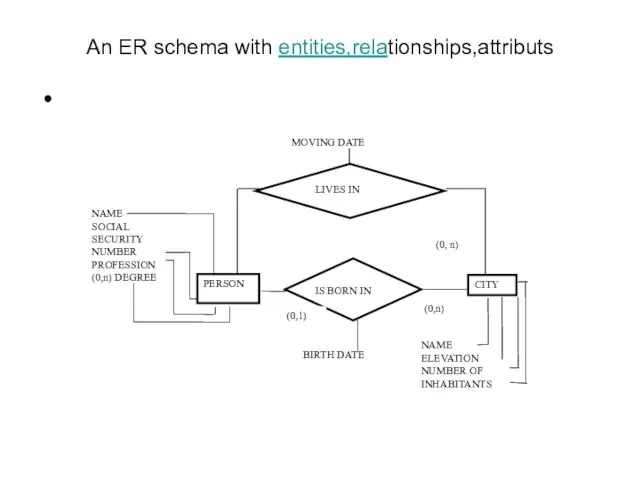
- 50. An ER schema with entities,relationships,attributs
- 51. An example of instance of DB schema PERSON={p1: , p2: P3: } CITY={c1: , c2: ,
- 52. Schema PERSONNEL Schema : PERSONNEL Entity: PERSON Attributes: NAME: text (50) SOCIAL SECURITY NUMBER: text (12)
- 53. Relationship: IS BORN IN Connected entities: (0,n) CITY (0,1) PERSON Attributes: BIRTH DATE: date
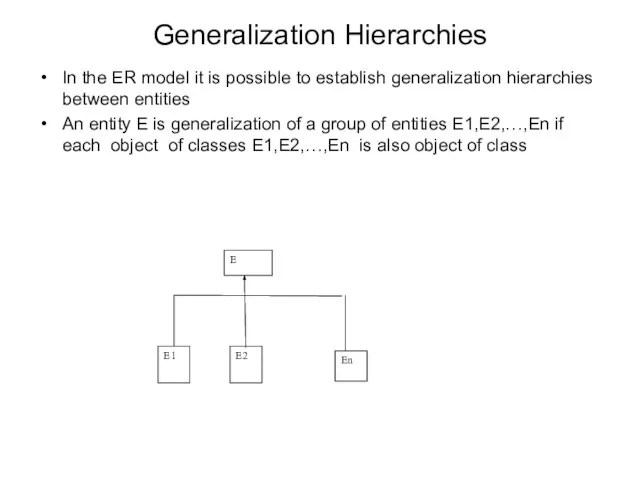
- 54. Generalization Hierarchies In the ER model it is possible to establish generalization hierarchies between entities An
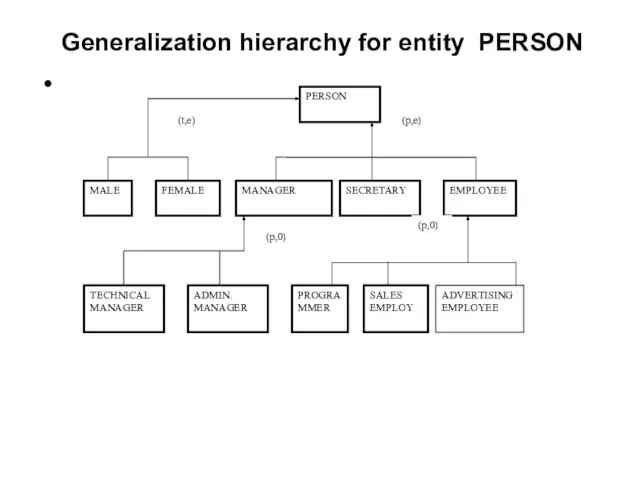
- 55. COVERAGE: Total generalization (t) Partial generalization (p) Exclusive (e) Overlapping (o) Pair: (t,e) the most frequently
- 56. Generalization hierarchy for entity PERSON
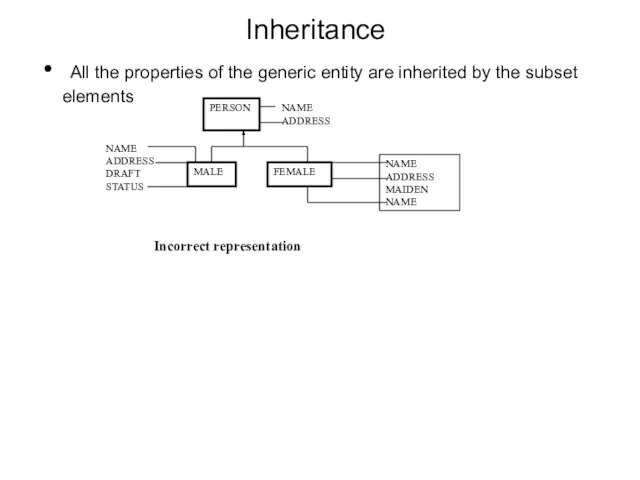
- 57. Inheritance All the properties of the generic entity are inherited by the subset elements PERSON NAME
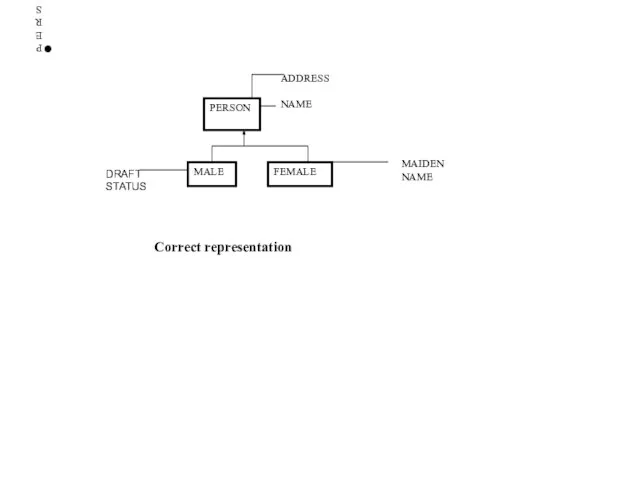
- 58. PERSON PERSON ADDRESS NAME DRAFT STATUS MALE FEMALE Correct representation MAIDEN NAME
- 59. Formal definition of Inheritance Let E be an entity. Let A1, A2,…,An be single valued, mandatory
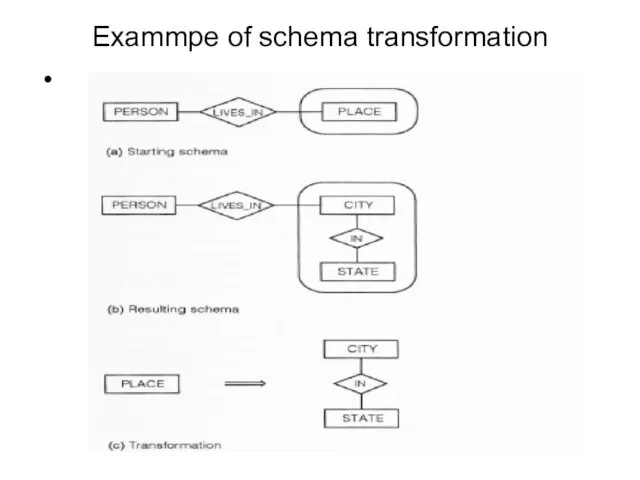
- 60. Exammpe of schema transformation
- 61. Each schema TRANSFORMATION has a starting schema and a resulting schema Each SCHEMA TRANSFORMATION maps names
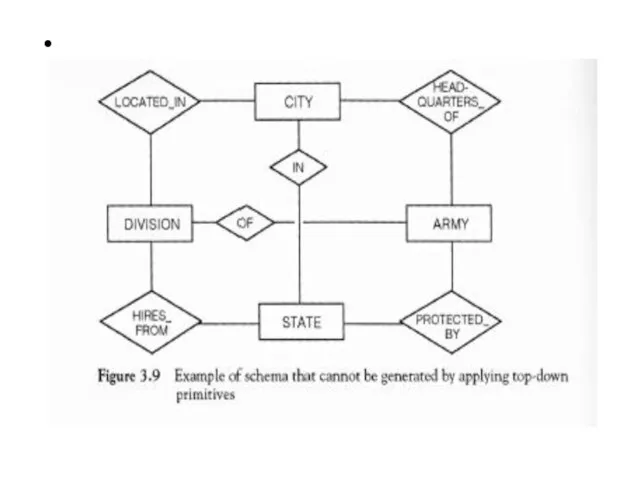
- 62. Properties of top –down primitives They have a simple structure: the starting schema is a single
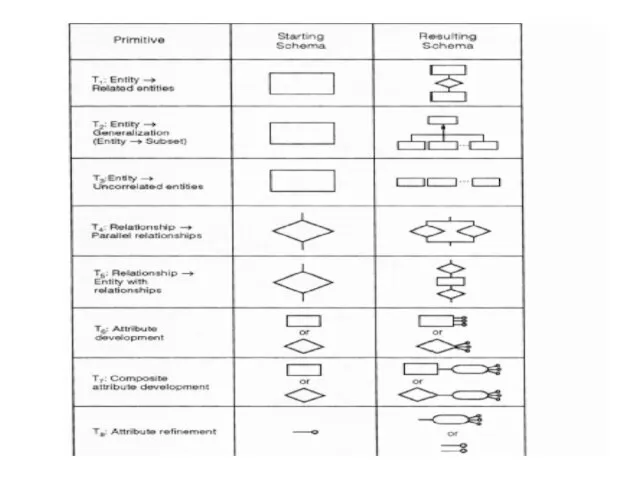
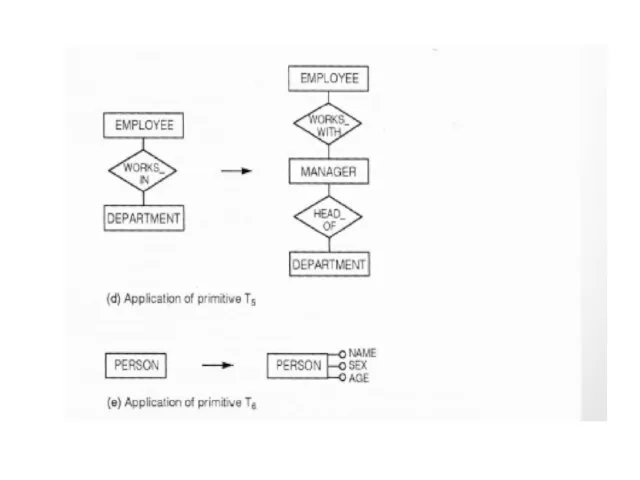
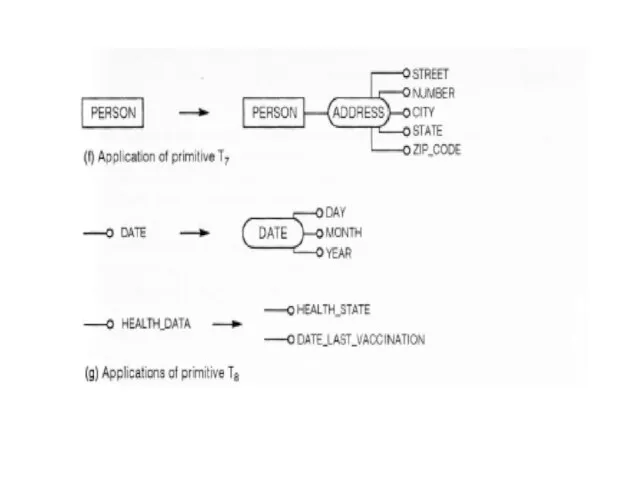
- 63. Top –Down Primitives
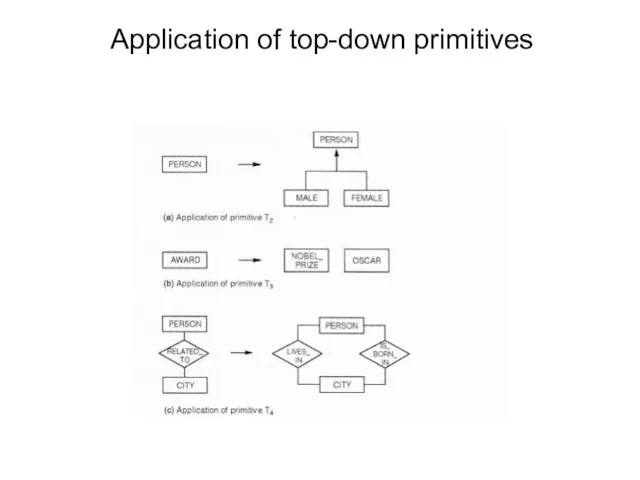
- 66. Application of top-down primitives
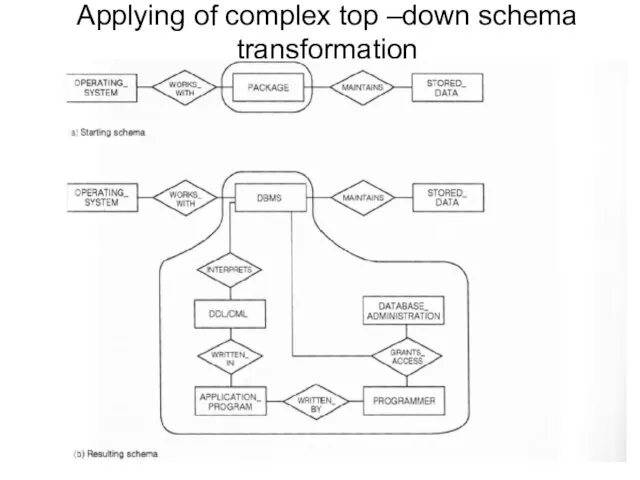
- 70. Applying of complex top –down schema transformation
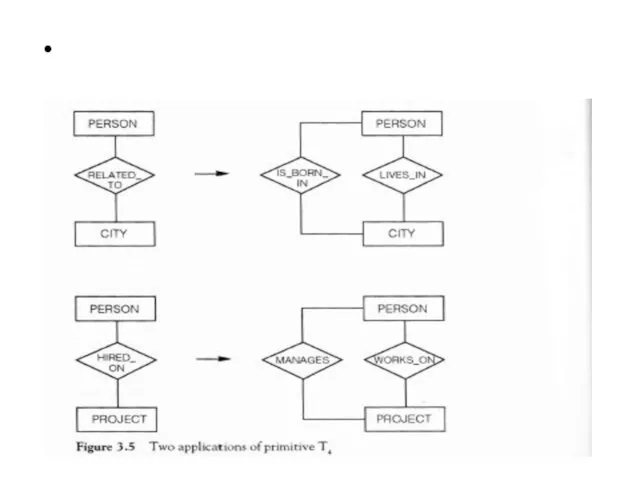
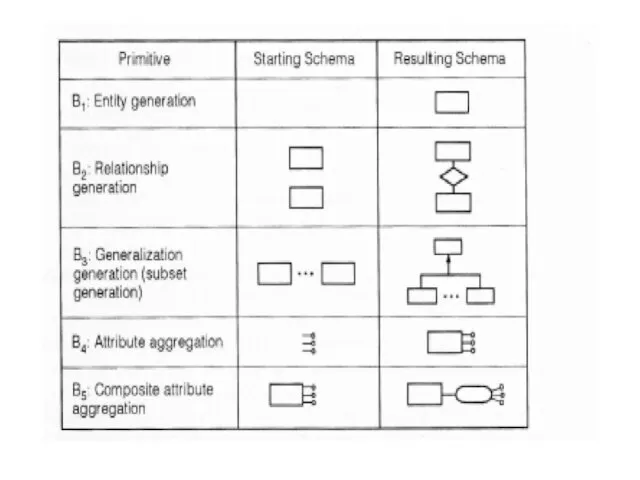
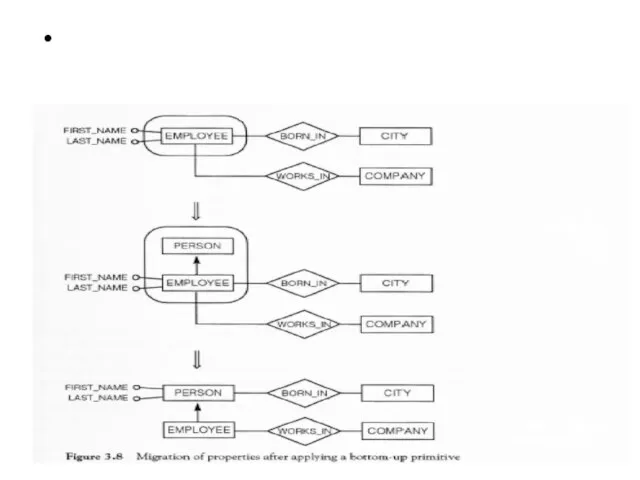
- 71. Bottom-up primitives
- 75. Strategies for Schema Design
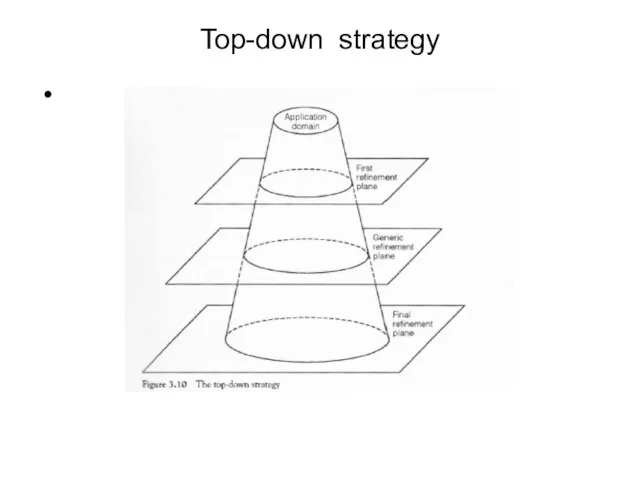
- 76. Top-down strategy
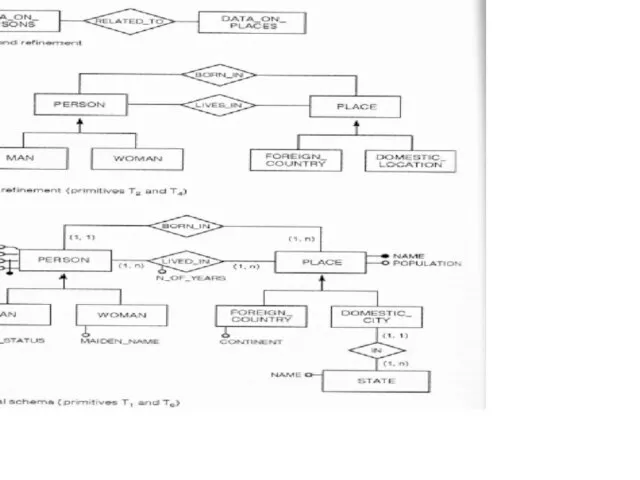
- 77. In the top-down strategy schema is obtained applying pure top-down refinement primitives
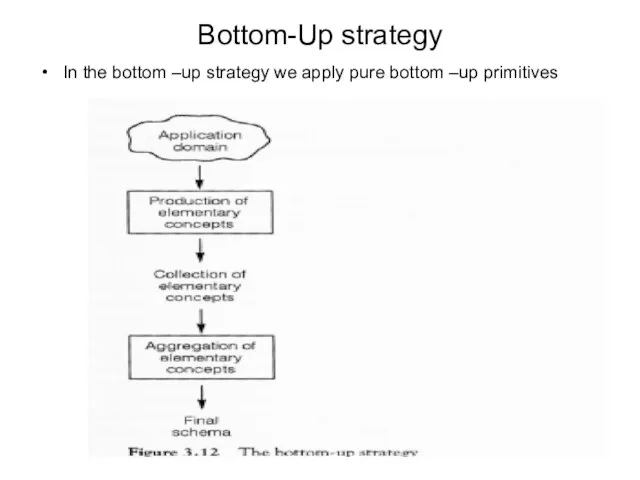
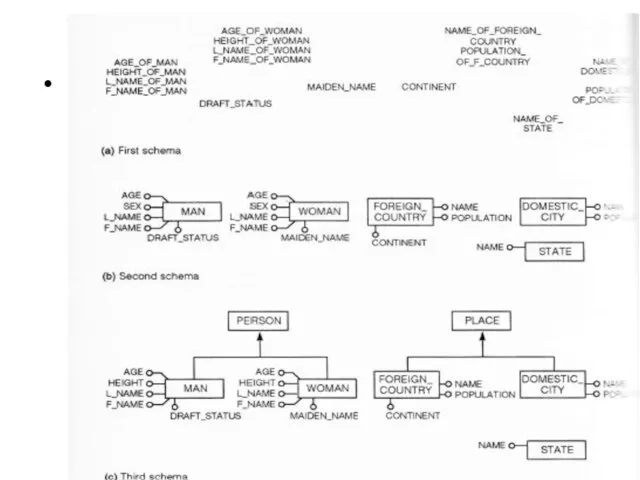
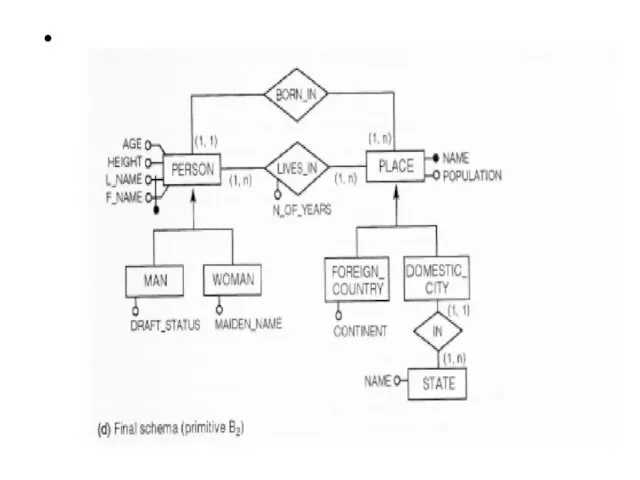
- 79. Bottom-Up strategy In the bottom –up strategy we apply pure bottom –up primitives
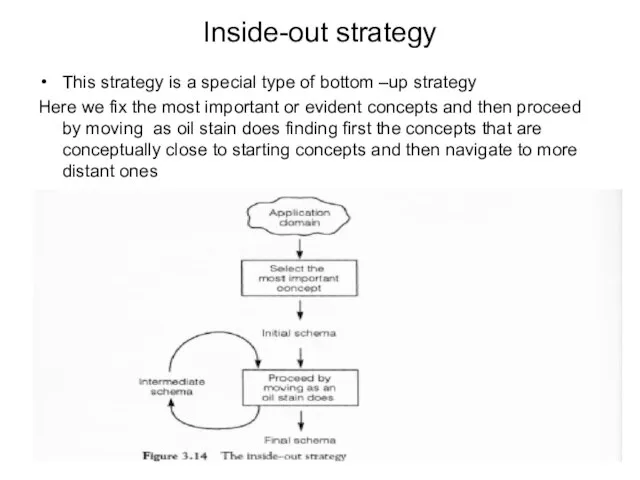
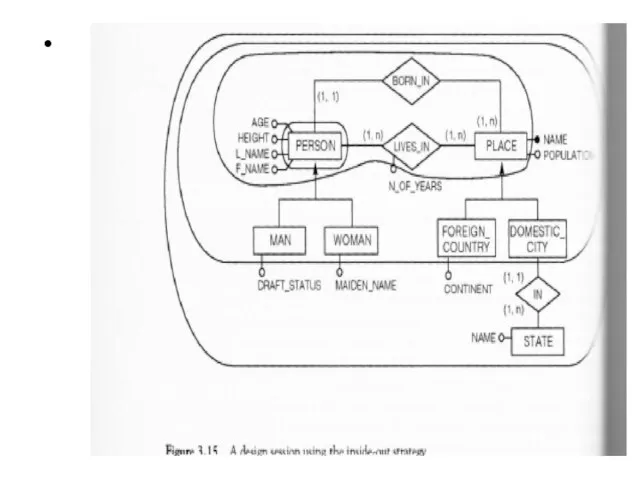
- 82. Inside-out strategy This strategy is a special type of bottom –up strategy Here we fix the
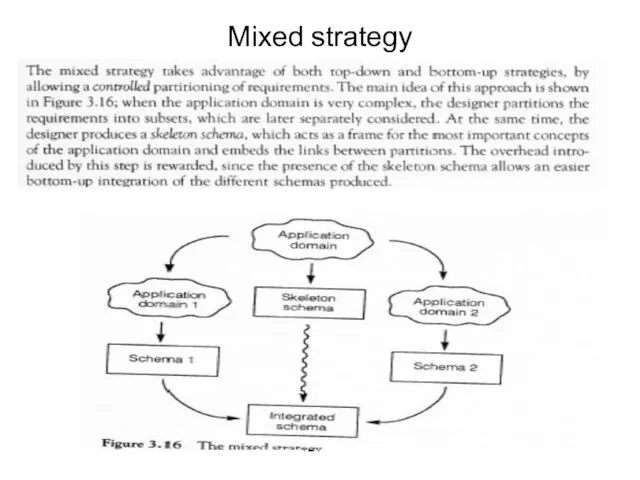
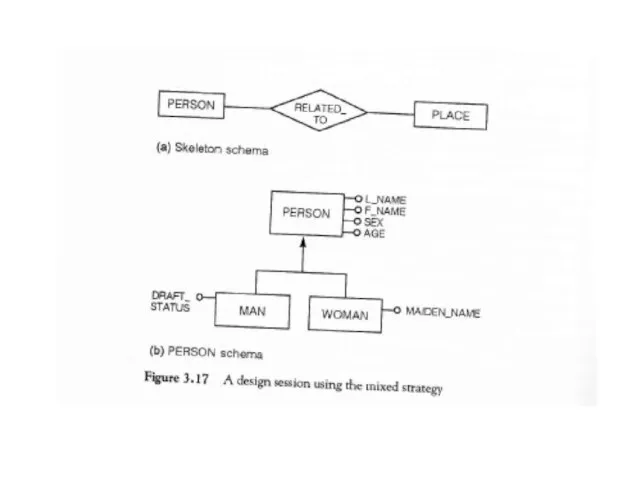
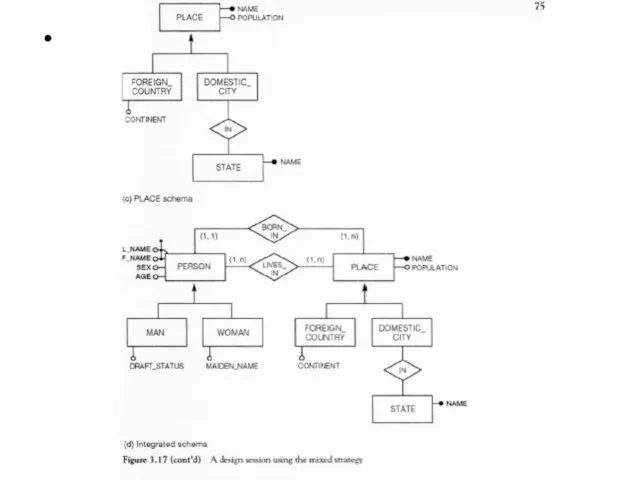
- 84. Mixed strategy
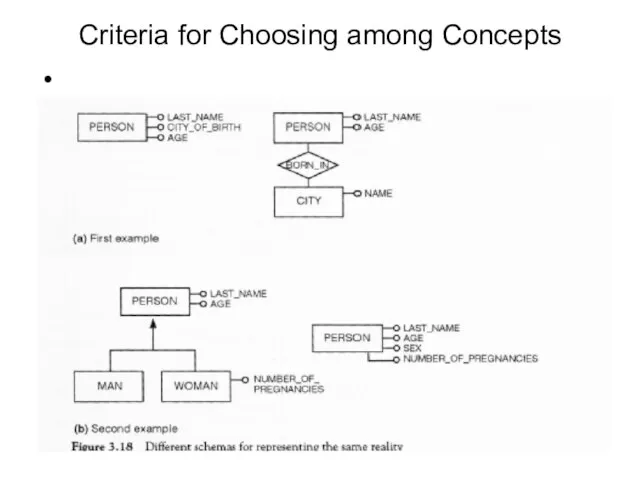
- 88. Criteria for Choosing among Concepts
- 89. Entity vs. Simple attribute
- 90. Generalization vs. attribute Generalization will be used when we expect that some property will be associated
- 91. Composite attribute vs set of simple attributes
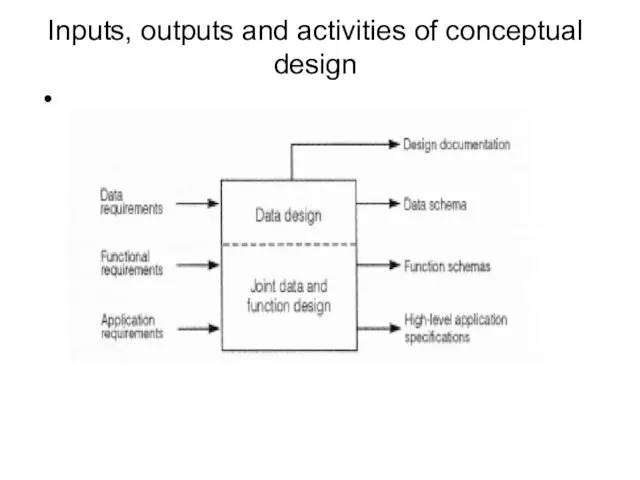
- 92. Inputs, outputs and activities of conceptual design
- 95. Outputs
- 97. Скачать презентацию




































 «Ви?дение» экономики в старом и новом институционализме
«Ви?дение» экономики в старом и новом институционализме Творческий портрет Ульяны Лопаткиной
Творческий портрет Ульяны Лопаткиной 4cde4c0ca65b9adc
4cde4c0ca65b9adc Почвенные ресурсы
Почвенные ресурсы Work and energy
Work and energy Диплом
Диплом Презентация на тему Петровские реформы
Презентация на тему Петровские реформы Кафедра английской филологии
Кафедра английской филологии Сатирические образы человека
Сатирические образы человека Карта Сбербанка для первокурсников Томского государственного университета
Карта Сбербанка для первокурсников Томского государственного университета Особенности эмоциональной сферы личности младших школьников, обучающихся в «компенсирующих» классах по коррекцинно- развивающим
Особенности эмоциональной сферы личности младших школьников, обучающихся в «компенсирующих» классах по коррекцинно- развивающим Huvitav ettevõte. Swarovski
Huvitav ettevõte. Swarovski Презентация на тему Зеленый лук
Презентация на тему Зеленый лук Информационная война виртуальность или реальность
Информационная война виртуальность или реальность Увидеть Париж. Финансовое планирование поездки
Увидеть Париж. Финансовое планирование поездки «P&G-Новомосковск»
«P&G-Новомосковск» Организационная структура Вооруженных Сил России
Организационная структура Вооруженных Сил России Компьютерная графика
Компьютерная графика Тире между подлежащим и сказуемым
Тире между подлежащим и сказуемым Человеческий труд в рассказе Никита
Человеческий труд в рассказе Никита Белорусская автокефальная православная церковь
Белорусская автокефальная православная церковь КЛАССИФИКАЦИЯ РЕЛИГИЙ
КЛАССИФИКАЦИЯ РЕЛИГИЙ 8. Effektlar va animatsiya
8. Effektlar va animatsiya Презентация на тему Синие горы Кавказа в жизни и творчестве М.Ю. Лермонтова
Презентация на тему Синие горы Кавказа в жизни и творчестве М.Ю. Лермонтова  Рязанский историко-архитектурный музей – заповедник «Рязанский Кремль» - презентация
Рязанский историко-архитектурный музей – заповедник «Рязанский Кремль» - презентация Презентация на тему: Антенны Выполнила: Булдакова С.Г. 271 гр.
Презентация на тему: Антенны Выполнила: Булдакова С.Г. 271 гр. Первая медицинская помощь при кровотечении
Первая медицинская помощь при кровотечении Скелет-опора организма
Скелет-опора организма