Интеграл и его практическое применение

Выполнил:
Ершов Николай,
ученик 11 класса.
Руководитель:
Дедовец Надежда Артемовна,
учитель математики
С. Большой Атлым
2012-2013 уч. год

Цель работы:
Расширить область математических знаний. Развивать логическое мышление.
Вывести общие формулы, позволяющие решать задачи интегрирования.
Показать, что интеграл широко применяется в различных сферах жизнедеятельности.

Задачи исследования:
- собрать, изучить и систематизировать материал об интеграле;
- рассмотреть, как интеграл используется при решении различных жизненных ситуаций;
- использование интеграла в различных сферах жизнедеятельности.
Объект исследования:
область математики – интегрирование.

Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
- 1675 г, Ж Лагранж
5 век до н.э. др.гр. ученый Демокрит
3-4 век до н.э. Архимед ввел метод исчерпывания

Евдокс Книдский
408 – 355 до н. э
Архимед
287 – 212 до н.э.
Строгое изложение теории интегралов появилось только в 19 веке. Но задачами на вычисление площадей занимались математики Древней Греции.
Математики Древней Греции

«Интеграл» придумал Я.Бернулли (1690)
«восстанавливать» от латинского integro
«целый» от латинского integer

Исаак Ньютон
(1643-1727)
Разумом он превосходил род человеческий. Лукреций

Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»
Лейбниц

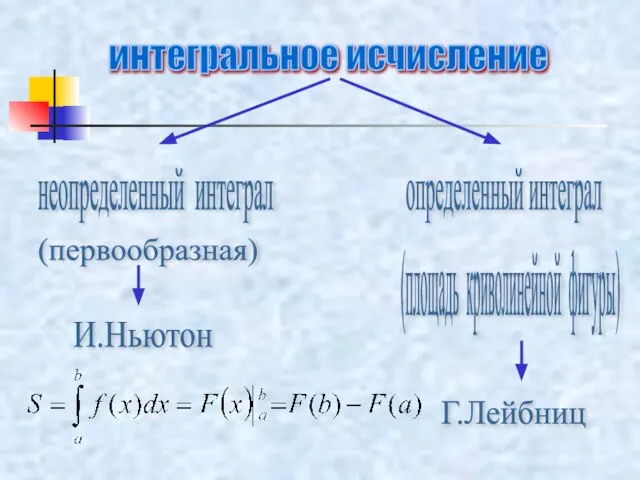
интегральное исчисление
неопределенный интеграл
определенный интеграл
(первообразная)
(площадь криволинейной фигуры)
И.Ньютон
Г.Лейбниц

Дифференцирование
Интегрирование
х(t)
v(t)
a(t)

Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Масса
Перемещение
Дифференциальное уравнение
Давление
Количество теплоты

Задача .Найти объём наклонной треугольной призмы с основанием S и
высотой h.
1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС)∩OX=a, a=0, (A1B1C1) ∩ OX=b, b=h
3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.
Ответ: V=Sh
4. S(x) непрерывна на [0;h]

Из эксперимента известно, что скорость размножения бактерий пропорциональна их количеству. За какое время количество бактерий увеличится в m раз по сравнению с начальным?
Решение:
Пусть x(t) – количество бактерий в момент времени t. x(0) = x0. Изменение количества бактерий со временем описывается уравнением
x´(t) = kx(t), k>0, ,
ln|x| = kt+ln|C|,
x=ekteln|C| , x=Cekt - общее решение уравнения.
ЗАДАЧА

y“=-ω²y – дифференциальное уравнение гармонических колебаний.
ω – заданное положительное число
y=y‘(x) y“=(y‘(x))‘
Решением являются функции:
Y(x)=Asin(ωx + φ), где
A – амплитуда колебания,
ω – частота, φ – начальная фаза.
Графиком гармонических колебаний является синусоида

Уже Архимед успешно находил площади фигур, несмотря на то, что в математике его времени не было понятия интеграла
Но лишь интегральное исчисление дает общий метод решения задач из различных областей наук.
Недаром даже поэты воспевали интеграл.
Смысл- там, где змеи интеграла
Меж цифр и букв , меж d и f.
Там – власть, там творческие горны!
Пред волей чисел все – рабы.
И солнца путь вершат, покорны
Немым речам и ворожбы.
В.Брюсов.