Интегралы.Методы интегрирования.

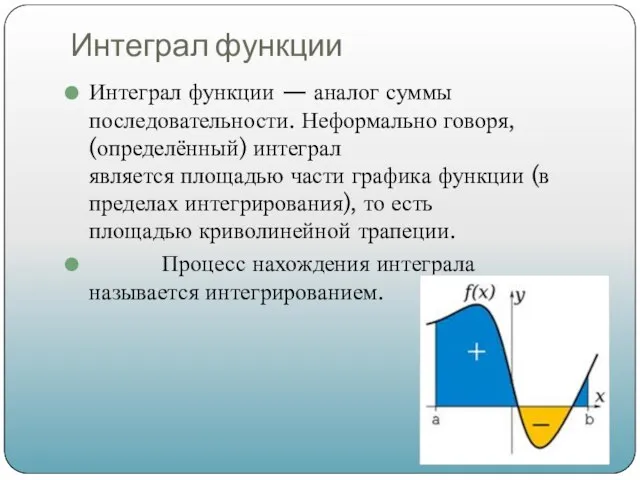
Интеграл функции
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
Процесс нахождения интеграла называется интегрированием.

Интеграл Римана
Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения. Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана. Графический смысл

Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г. до н.э, Московский математический папирус демонстрирует знание формулы объёма усеченной пирамиды.

Первым известным методом для расчета интегралов является метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны.

Этот метод был подхвачен и развит Архимедом, и использовался для расчета площадей, парабол и приближенного расчета площади круга.
. Аналогичные методы были разработаны не зависимо в Китае в 3-м веке н.э. Лю Хуэйем, который использовал их для нахождения круга.

Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для нахождения объема шара
Следующий крупный шаг в исследование интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсаном ( известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени.
Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени.

Методы интегрирования

Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных пpeобpaзoвaний подынтегральной фyнкции (или выражения) и применения свойств нeoпpеделeннoгo интеграла приводится к oдиoмy или нескольким табличным интегралам, называется нeпоcpeдcтвeнным uнmeгpирoванием.При сведении даннoгo интеграла к табличному часто используются следующие пpeoбpазoвания диффeренциaлa (операция «подвeдeния под знак дuффepeнциала»):
Boобщe, ƒ'(u)du=d(ƒ(u)), эта
формула очень частo используется при вычислении интегралов.

Примеры:
1

Метод интегрирования подстановкой (заменой переменной)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводащимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно oпpeделить подстановку пpиобpетaeтcя практикой.

Пусть тpебyетcя вычислить интеграл
Сделаем подстановку
х =φ(t), где φ(t) - функция, имеющая непрерывную производную.
Тогда dx=φ'(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй
Тогда dx=φ'(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй
(30.1)

Формула (30.1) также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде t= φ(х), тогда
Другими слoвaми, формулу (30.1) можно применять справа налево

Метод интегрирования по частям
Пусть u=u(х) и ν=v(х) - функции, имеющие непрерывные производные. Тогда d(uv)=u•dv+v•du.Интегрируя это равенство, получим
Полученная формула называется формулой интегрирования по частям. Она дает возможность свести вычисление интеграла к вычислению интеграла , который может оказаться существенно более простым, чем исходный.

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо обpaзoм в виде произведения двух сомножителей и и dv (это, как правило, можно осуществить несколькими cспособами); затем, после нахождения ν и du, используется формула интегрирования по частям. Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удюбно вычислять методом интегрирования по частям.

Укажем некоторые типы интегралов, которые удюбно вычислять методом интегрирования по частям.
1. Интегралы вида где
Р(х) - многочлен, К - число. Удобно положить u=Р(х), а за dv обoзнaчить все остальные сомножители.
2.Интегралы вида
Удобно положить Р(х)dx=dv, а за u обозначить остальные сомножители.
3. Интегралы вида , где а и b - числа.
За и можно принять функциюu=еαх.

Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Масса
Перемещение
Дифференциальное уравнение
Давление
Количество теплоты