Содержание
- 2. План: Точность оценки. Доверительная вероятность (надежность). Доверительный интервал. Интервальные оценки параметров нормального распределения. Доверительный интервал для
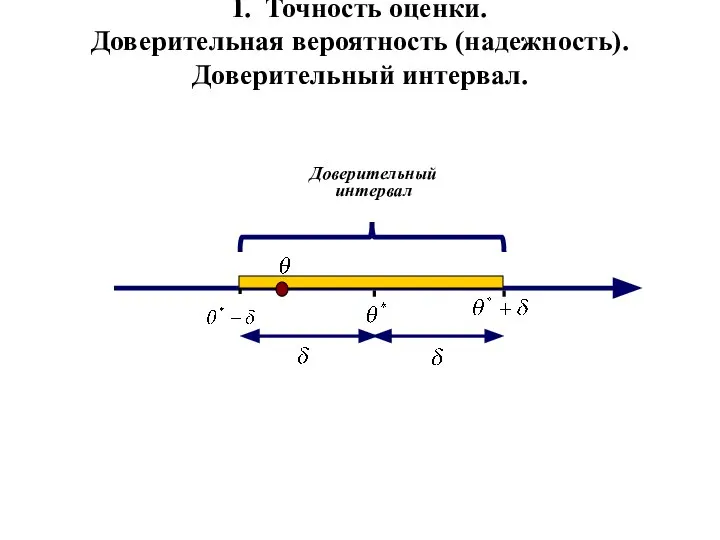
- 3. I. Точность оценки. Доверительная вероятность (надежность). Доверительный интервал. γ – доверительная вероятность (надежность оценки) δ >
- 4. I. Точность оценки. Доверительная вероятность (надежность). Доверительный интервал. Доверительный интервал
- 5. Ежи Нейман (1894-1981) Рональд Фишер (1890-1962)
- 6. II. Интервальные оценки параметров нормального распределения. X~N(a,σ)
- 7. 1) Доверительный интервал для оценки математического ожидания при известном σ Дано: случайная выборка объема n из
- 8. 1) Доверительный интервал для оценки математического ожидания при известном σ - точность оценки; - значение аргумента
- 9. ПРИМЕР 1. Случайная величина прочности бетона X имеет нормальное распределение с известным стандартом σ = 3
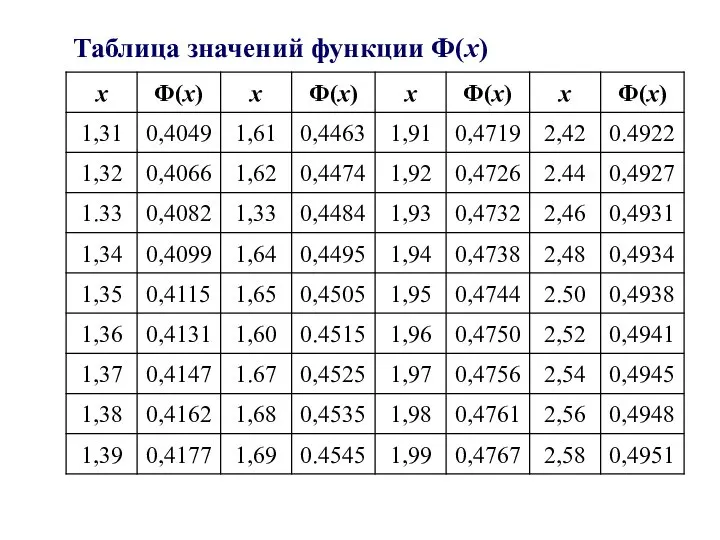
- 10. Таблица значений функции Ф(х)
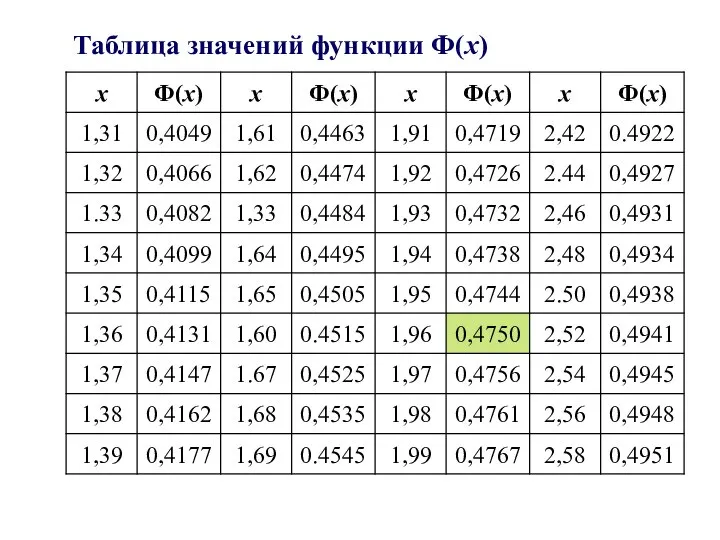
- 11. Таблица значений функции Ф(х)
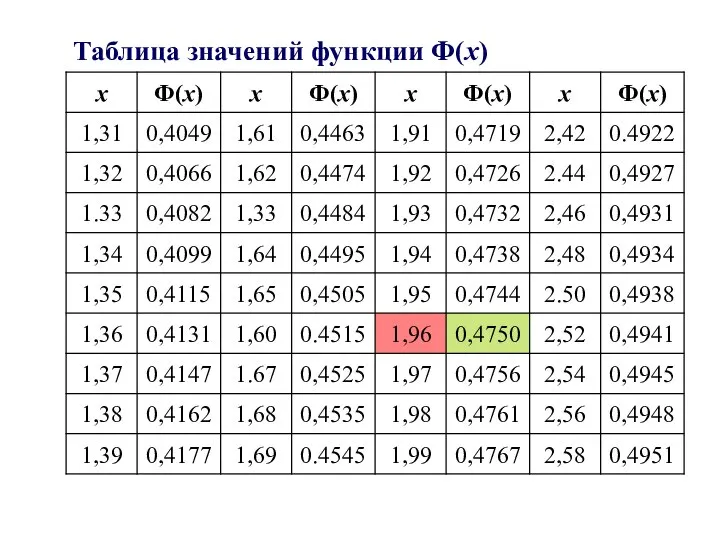
- 12. Таблица значений функции Ф(х)
- 13. ПРИМЕР 2. Найти минимальный объем выборки, на основании которой можно было бы оценить параметры некоторой технической
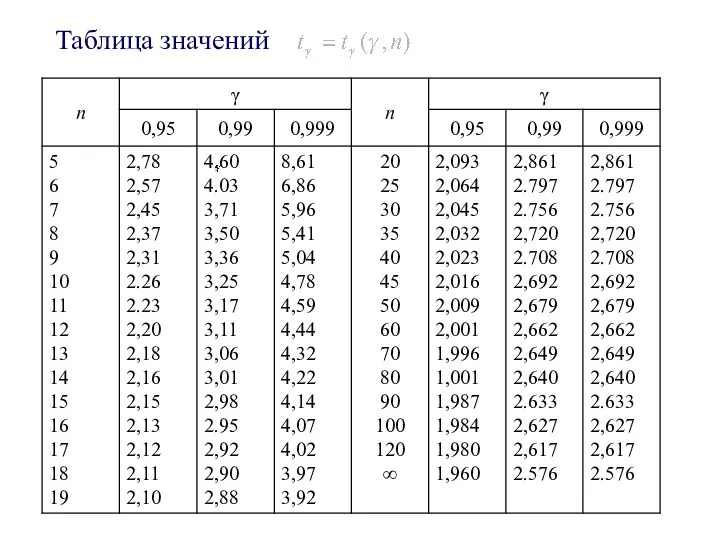
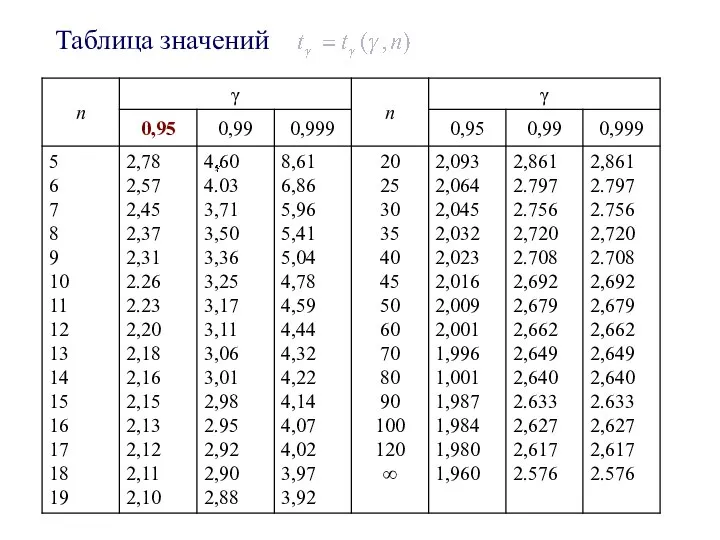
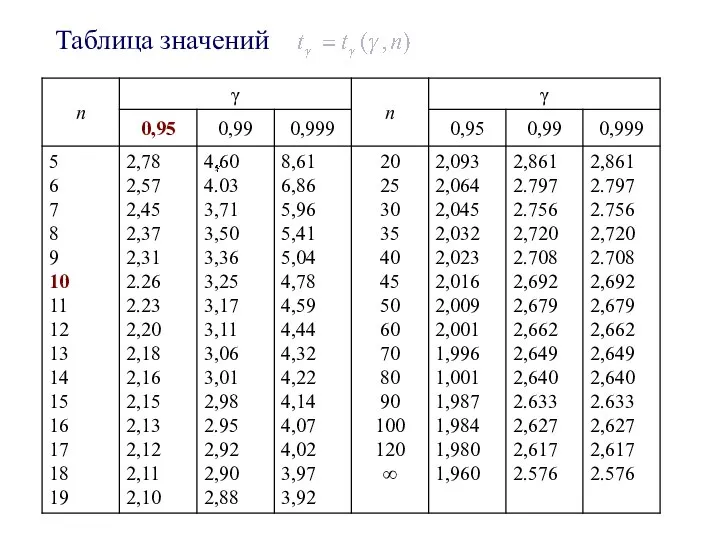
- 14. 2) Доверительный интервал для оценки математического ожидания при неизвестном σ X~N(a,σ), -определяется по «Таблице значений »
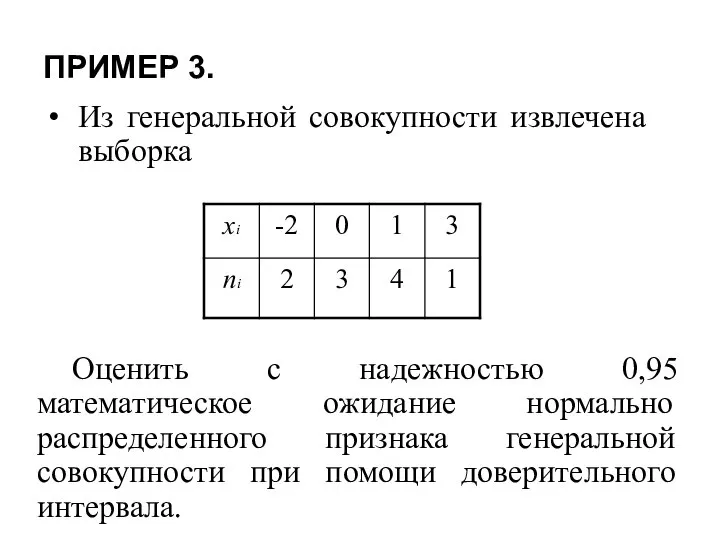
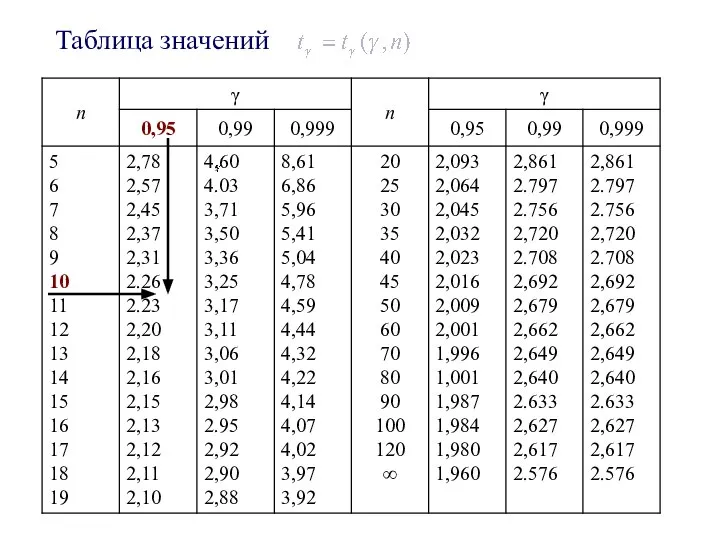
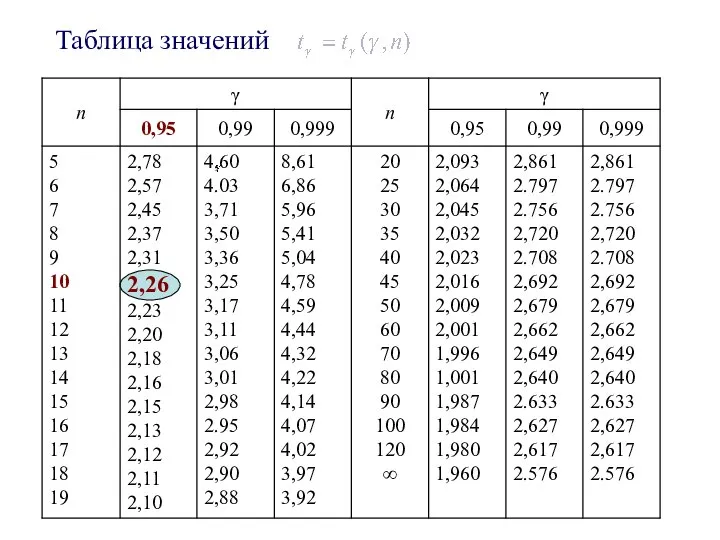
- 15. ПРИМЕР 3. Из генеральной совокупности извлечена выборка Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака
- 16. Таблица значений
- 17. Таблица значений
- 18. Таблица значений
- 19. Таблица значений
- 20. Таблица значений
- 21. 3) Доверительный интервал для оценки среднего квадратического отклонения σ нормально распределенного количественного признака X с заданной
- 22. ПРИМЕР 4. Количественный признак X генеральной совокупности распределен нормально. По выборке объема п = 25 найдено
- 24. Скачать презентацию











 Презентация на тему Золотое правило механики
Презентация на тему Золотое правило механики  Методы улучшения систем теплоснабжения
Методы улучшения систем теплоснабжения Век Елизаветы
Век Елизаветы Праздничная дискотека «Новогодняя тусовка»
Праздничная дискотека «Новогодняя тусовка» Неоэкспрессионизм. История современной архитектуры
Неоэкспрессионизм. История современной архитектуры Зеленая Волна - это…
Зеленая Волна - это… Физическая культура. Викторина
Физическая культура. Викторина Маркетинговый План. Краеугольный камень продаж. Гостиничных продаж и управления доходами
Маркетинговый План. Краеугольный камень продаж. Гостиничных продаж и управления доходами Серебряный век русской культуры
Серебряный век русской культуры Оверлеппинг
Оверлеппинг Каротаж на бурильных трубах
Каротаж на бурильных трубах Тема: «Законодательное обеспечение системы образования в условиях модернизации»
Тема: «Законодательное обеспечение системы образования в условиях модернизации» Настройка VPN
Настройка VPN Отчеты стран Центральной Азии о выполнении Декларации о приверженности (ССГАООН)
Отчеты стран Центральной Азии о выполнении Декларации о приверженности (ССГАООН) Презентация на тему Мастер - классе по созданию мягкой игрушки
Презентация на тему Мастер - классе по созданию мягкой игрушки Демократизасийа вя авторитарлыг
Демократизасийа вя авторитарлыг Особенности питания животных
Особенности питания животных Теория панспермии
Теория панспермии Устройство токарного станка по дереву JET JWL-1440L. 6 класс
Устройство токарного станка по дереву JET JWL-1440L. 6 класс Презентация на тему: Подлежащее. Способы выражения подлежащего 5 класс
Презентация на тему: Подлежащее. Способы выражения подлежащего 5 класс Презентация на тему Комплексно-тематическое планирование образовательного процесса в ДОУ
Презентация на тему Комплексно-тематическое планирование образовательного процесса в ДОУ "Предварительные установки, или Организационные рамки семинара"
"Предварительные установки, или Организационные рамки семинара" Частушки. 2 класс
Частушки. 2 класс Феномен портфолио
Феномен портфолио Основные направления развития законодательства о кредитной кооперации17 ноября 2009 г.г. Москва
Основные направления развития законодательства о кредитной кооперации17 ноября 2009 г.г. Москва Направление подготовки Международные отношения
Направление подготовки Международные отношения Гражданин должен знать свою Родину
Гражданин должен знать свою Родину Игра по географии
Игра по географии