Исследование математических моделей процессов жизненного цикла технической инновации

Цель магистерской диссертации:
Анализ математических моделей процессов жизненного цикла технической инновации, а также моделирование основных показателей процессов жизненного цикла технической инновации и оценка полученных результатов.
Задачи магистерской диссертации:
исследование математической модели финансового обеспечения процесса производства технической инновации;
исследование математической модели процесса реализации технической инновации;

Динамическая модель финансового обеспечения процесса производства технической инновации
(1)
(3)

Динамическая модель финансового обеспечения процесса производства технической инновации
(1)
(3)
M – выручка от реализации продукта;
m – отражает производственные издержки;
cij – время оборота средств;;
eij –объем внешних заимствований;
ij – кредитная ставка;
– доля оборотных средств, затрачиваемая на хранение единицы готовой продукции в единицу времени

Динамическая модель финансового обеспечения процесса производства технической инновации

Бифуркационный анализ динамической модели финансового обеспечения
Рассмотрим особые точки системы (5):

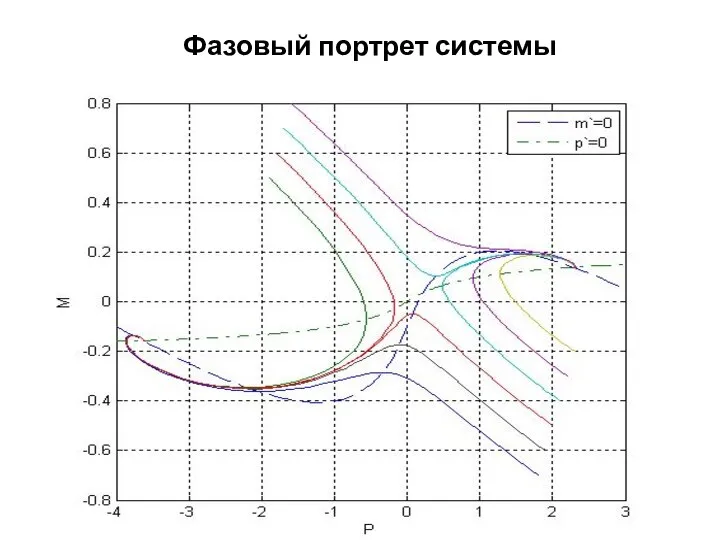
Фазовый портрет системы

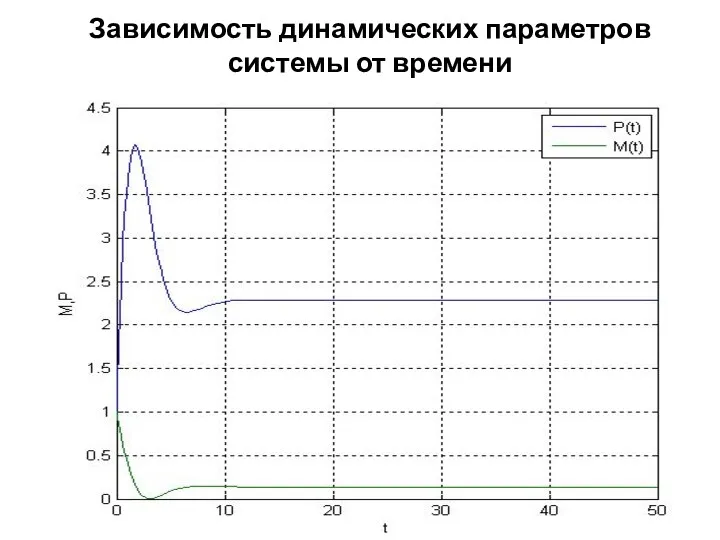
Зависимость динамических параметров системы от времени

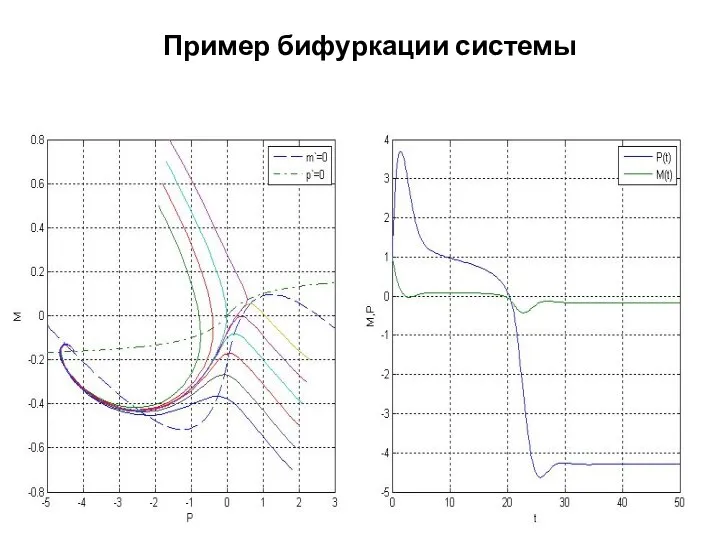
Пример бифуркации системы

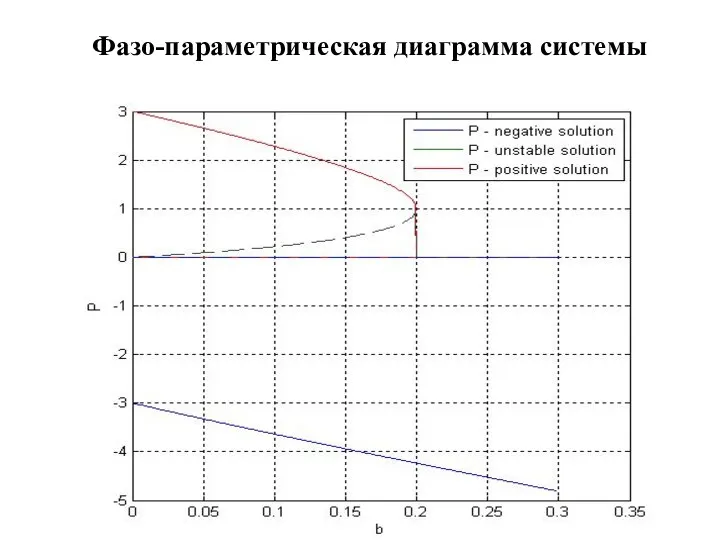
Фазо-параметрическая диаграмма системы

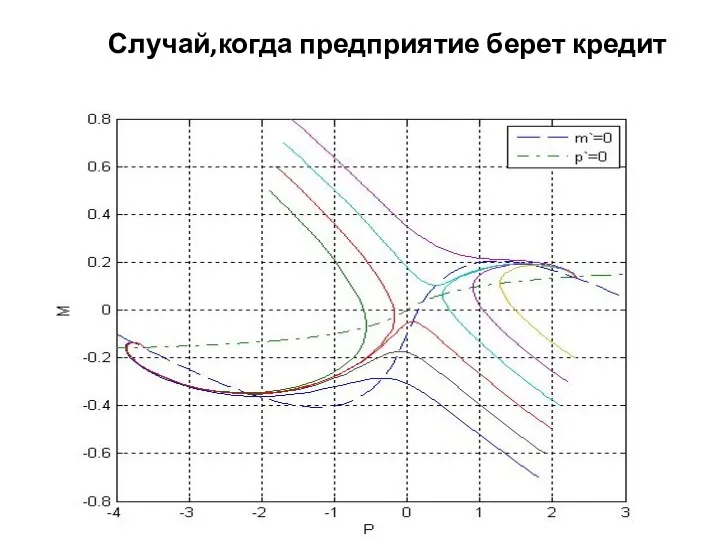
Случай,когда предприятие берет кредит

Определение оптимальной структуры источников финансирования
(4)
(5)
при ограничениях:
где m – число возможных источников финансирования;
rk – стоимость k-го источника финансирования;
wk – удельный вес k-го источника финансирования;
Wk – максимальный доступный удельный вес k-го источника финансирования;
riskk– риск неполучения финансирования из k-го источника;
riskmax – максимально допустимый риск неполучения финансирования;
R – рентабельность реализуемого проекта;
t(wk) – время привлечения средств из k-го источника финансирования;
Cj – средства необходимые в j-й период проекта;
Cпл – средства необходимые на весь проект;
tj – допустимое время привлечение средств для j-го периода проекта.

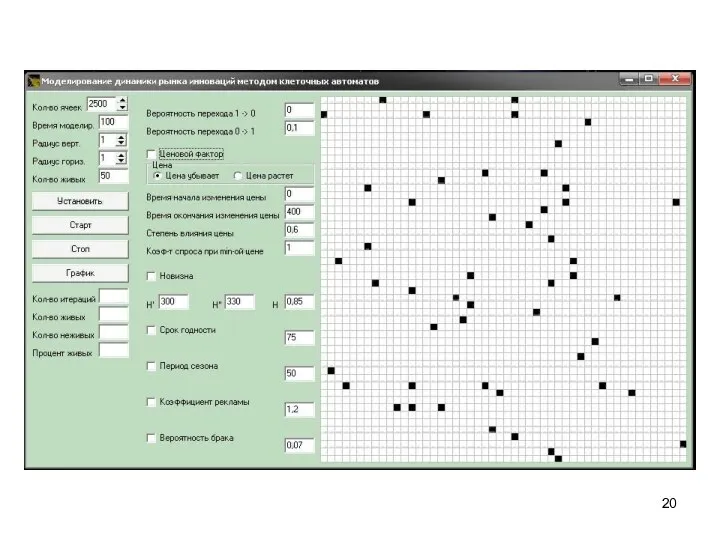
Исходные данные

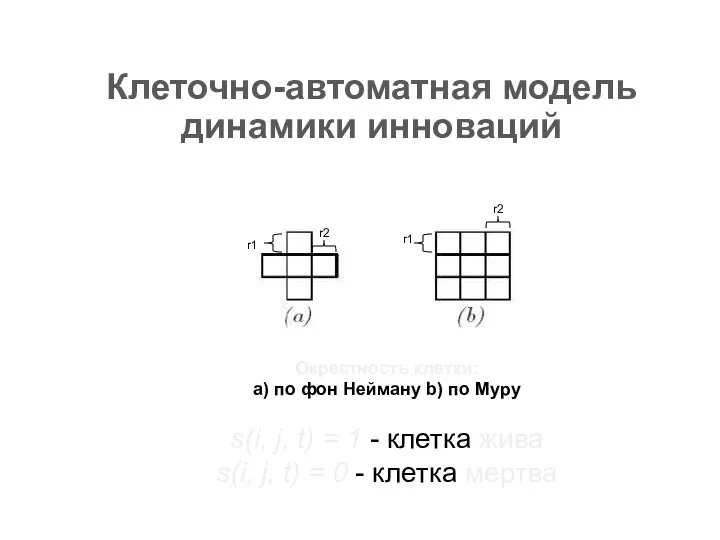
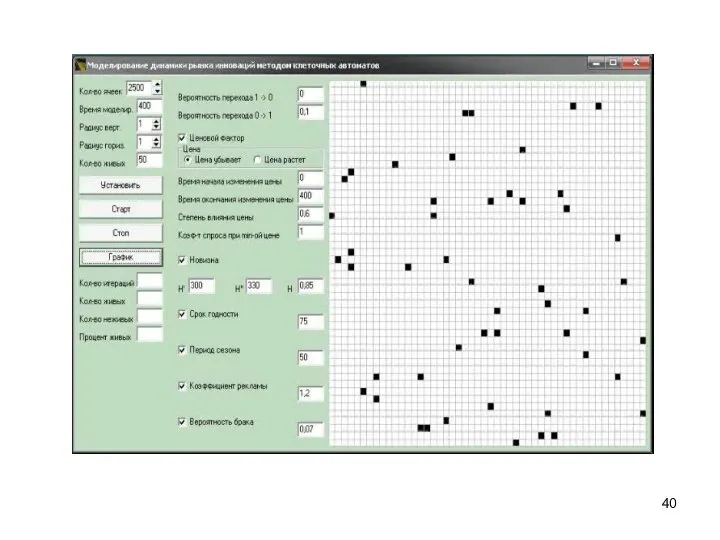
Клеточно-автоматная модель динамики инноваций
s(i, j, t) - состояние s клетки с координатами
(i, j) в момент времени t
okr – количество клеток, входящих в
окрестность клетки + 1 (сама клетка)

Окрестность клетки:
a) по фон Нейману b) по Муру
s(i, j, t) = 1 - клетка жива
s(i, j, t) = 0 - клетка мертва
Клеточно-автоматная модель динамики инноваций
r1
r2
r1
r2

Правило №1:
Состояние клетки с координатами
(i, j) в момент времени t+1 зависит от плотности соседних живых клеток, входящих в окрестность (r1, r2) на предыдущем шаге t.

Плотность σ(i, j, t) по Муру:
Правило №1:
Матрица перехода:
Pa←b - вероятность изменения состояния клетки с b на a

Правило №2:
Вероятность обладателя инновации
отказаться от нее равняется некоторому заранее
заданному числу p ( ), зависящему от вида продукта, для которого проводится моделирование, текущего состояния потребителя и его окружения. Вероятность же объекта, не обладающего инновацией, приобрести его пропорциональна плотности окружения соседних клеток, с коэффициентом пропорциональности
q ( ), и их текущего состояния.

Правило №2:
Матрица перехода:

Правило №3:
Вероятности принятия и отторжения инновации ее потенциальным потребителем напрямую зависят от степени новизны этого продукта.

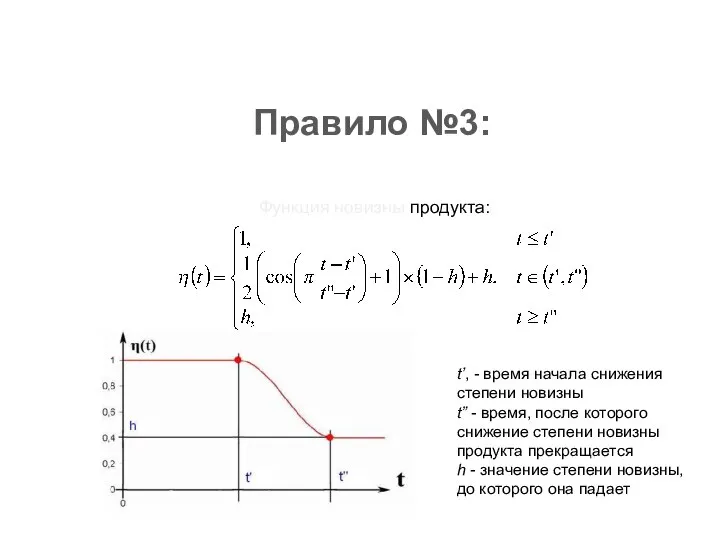
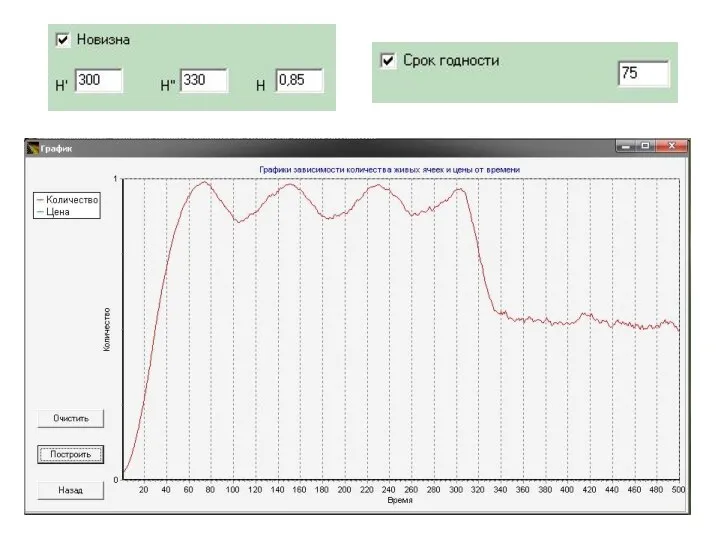
Правило №3:
Функция новизны продукта:
t’, - время начала снижения степени новизны
t” - время, после которого снижение степени новизны продукта прекращается
h - значение степени новизны, до которого она падает

Правило №3:
Матрица перехода:

Правило №4:
Потенциальный потребитель,
приобретший инновацию, по истечению заданного периода времени перестает быть ее обладателем, так как она приходит в негодное состояние, либо перестает отвечать его интересам.

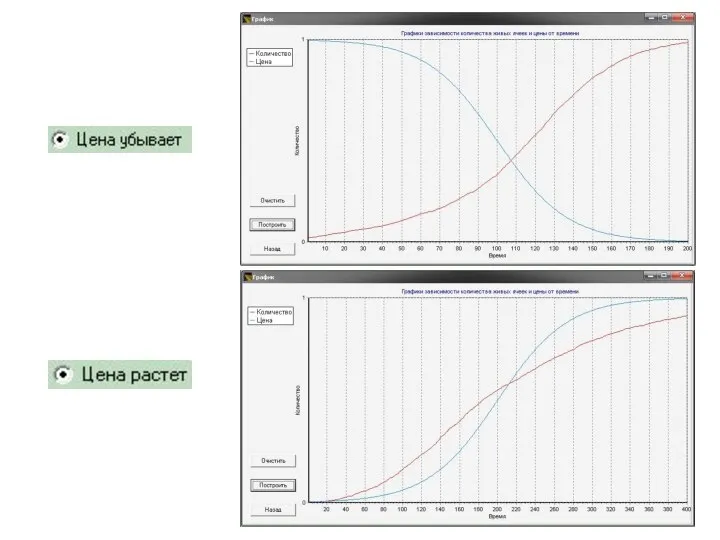
Правило №5:
Спрос на инновацию обратно пропорционален цене на нее.

Правило №5:
β(t) – коэффициент вероятности приобретения инновации:
Функция y(t) определяет цену в момент времени t:
p1 и p2 – моменты времени, когда изменение цены начинается и прекращается,
ω – коэффициент спроса при минимальной цене.
α – степень влияния цены на спрос

Правило №5:
Матрица перехода:

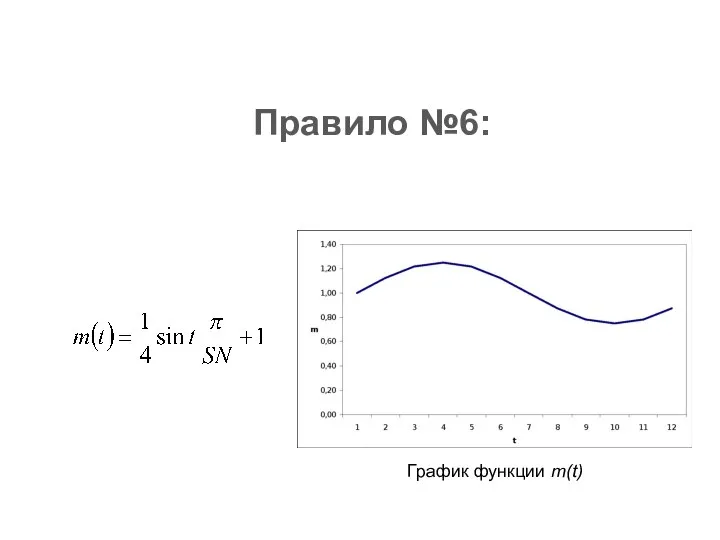
Правило №6:
Большинство товаров и услуг обладают сезонной актуальностью, что подразумевает неоднородность спроса на товар в течение определенных периодов времени.

Правило №6:
График функции m(t)

Правило №6:
Матрица перехода:

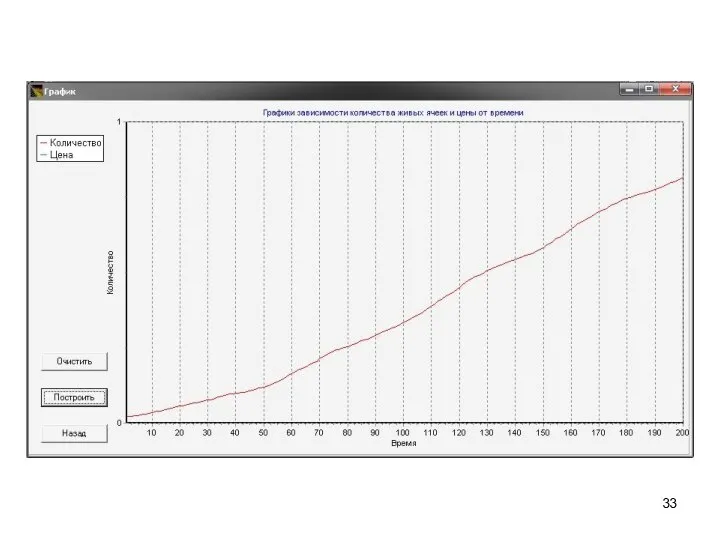
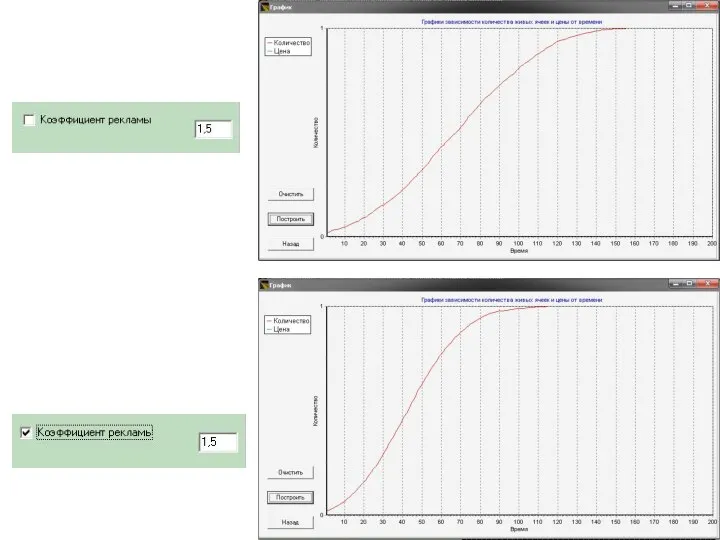
Правило №7:
Правило 7: Спрос на инновацию растет за счет рекламы компанией инновации.

Правило №7:
Матрица перехода:
коэффициент рекламы инновации, при увеличении которого спрос на
инновацию повышается

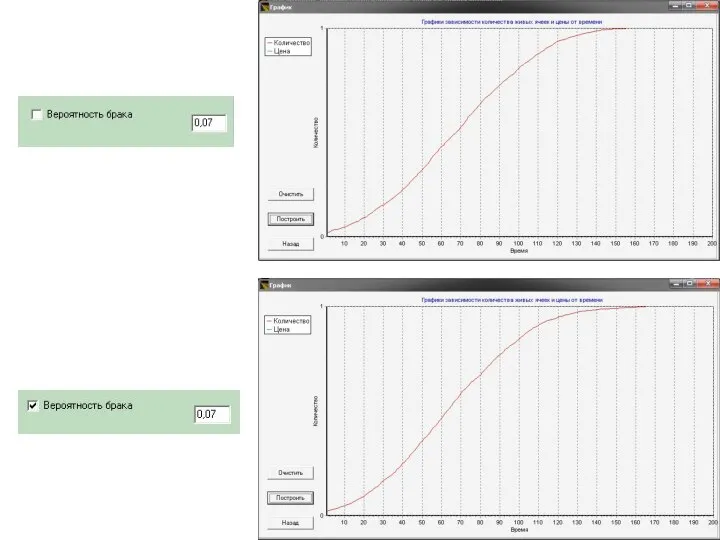
Правило №8:
Правило 8: Согласно исследованиям в области
социальной психологии, в случае наличия дефекта
одного из продуктов, доверие к торговой марке,
под которой он был выпущен, а значит и желание
потребителя пользоваться товарами и услугами,
выходящими под ней, снижается на 90%.

Правило №8:
Матрица перехода:

Выводы
разработана нелинейная динамическая модель диффузии инноваций;
разработана программа, реализующая данную модель;
выполнен анализ полученных результатов на основе графиков;
произведена оценка эффективности метода клеточных автоматов как способа моделирования динамики рынка инноваций.