Измерительная техника

Раздел 1. Основы метрологии
Тема 3: Виды погрешностей. Обработка результатов измерения
Виды погрешностей. Что называется погрешностью?
Обработка результатов измерения.
3. Обработка результатов измерения при косвенных методах

1. Виды погрешностей. Что называется погрешностью?

классификация погрешности измерений
По источнику (причине ) возникновения погрешности измерений делят :
-Инструментальная обусловлена конструктивными недостатками измерительных приборов и мер, их неправильной градуировкой или их неисправностью.

Методическая погрешность измерений — вызвана несовершенством выбранного метода измерений.
Методическая составляющая погрешности определяется несовершенством метода измерения, приемами использования СИ, некорректностью расчетных формул и округления результатов
и другими факторами, не связанными со свойствами СИ.

-Субъективная (личная) погрешность измерения -обусловленная индивидуальными особенностями оператора, т. е. погрешность отсчета оператором показаний по шкалам СИ.
Они вызываются состоянием оператора, несовершенством органов чувств, эргономическими свойствами СИ.

2.по характеру появления:
2.1-Систематические;
Систематические погрешности имеют повторяющийся характер при определении одной и той же величины.
2.2 - Случайные;
Случайные погрешности неопределенные по значению и знаку, возникают в результате действия неизвестных причин. Причины вызвавшие их могут быть самыми разнообразными, и не поддаются прогнозированию.

3-Промахи ( грубые)
Грубые погрешности возникают при внезапном изменении условий проведения эксперимента, например отключения установки. (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).
Грубая погрешность значительно превышает ожидаемую ПИ. Иногда грубую ПИ называют промахом.

3.По взаимодействию изменений во времени и входной величины погрешности делятся на
Статическая погрешность - это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.
Динамическая погрешность это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).

По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.
Основная погрешность - это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).
Дополнительная погрешность - это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.

По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.
Аддитивная погрешность - это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).
Мультипликативная погрешность - это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям

По способу выражения их делят на абсолютные и относительные погрешности измерений.

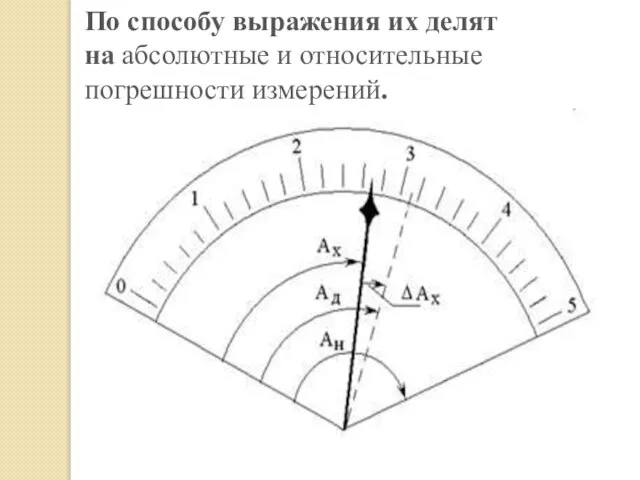
Абсолютная погрешность измерения ∆ равна разности между результатом измерения Аизм. и действительным значением измеряемой величины
∆А= /Аизм.-Ад /

Классом точности средства измерений называют обобщенную характеристику средства измерений, определяемую пределами допускаемых основных и дополнительных погрешностей.
класс точности- величина показывающая на допустимое отклонение в процентах

Основная погрешность – это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).
Дополнительная погрешность – это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.
Нормальные условия – это условия, в которых все значения влияющих величин являются нормальными либо не выходят за границы области нормальных значений.

Абсолютная погрешность , взятая с обратным знаком называется поправкой С
С=-∆А
Поправка – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Поправочный множитель – числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.

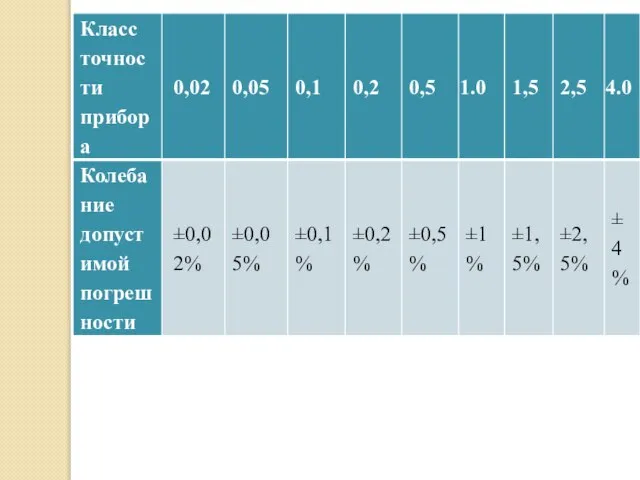
Однако класс точности прибора не определяет точность самого измерения.
δнаиб = γпр· Ан/Аизм. .
Полученное выражение показывает , что относительная погрешность измерения δнаиб во столько раз больше класса точности прибора γпр, во сколько раз номинальное значение прибора Ан больше измеряемого значения Аизм При измерении электрических величин, близких к номинальному значению прибора (Ах ~ Ан), относительная погрешность измерения δнаиб приближается к классу точности прибора γпр, а при измерении величин, малых по сравнению с номинальным значением прибора Ан, δнаиб может быть во много раз больше класса точности прибора.

Пример. Вольтметром класса 1,0 с номинальным значением Uн=250В измеряют напряжение U1=50В и U2=200В.
В первом случае погрешность измерения будет:
1. δнаиб = γпр ·Uн/U1=1,0·250/50=5%
Во втором случае:
2. δнаиб = γпр·Uн/U2=1,0·250/200=1,25%
Поэтому для повышения точности измерения следует пользоваться приборами, у которых измеряемая величина отсчитывалась бы во второй половине шкалы. Это позволяет осуществлять измерения с погрешностью, не превышающей удвоенного значения класса точности прибора.

Обработка результатов при косвенных методах
косвенный метод это когда величина определяется по формулам в которые входят значения величин измеренных непосредственно
2.2.1 Предположим , что искомая величина А и измеренные непосредственным способом величины связаны соответствием
-если А=Вп * Сm δА=nδВ + mδС