Содержание
- 2. Цели и задачи проекта Проиллюстрировать применение математики на практике Показать связь с другими областями знаний Познакомить
- 4. Понятие графов Всем известно, что слово «граф» означает дворянский титул, например граф Лев Николаевич Толстой. А
- 5. Немного из истории Появление теории графов как математической дисциплины, все единодушно относят к 1736 году, когда
- 6. Примерно в середине XIX века немецкий физик Г. Кирхгоф (1824-1871, иностранный член-корреспондент Петербургской академии наук разработал
- 7. Немного из истории Ещё одна проблема была сформулирована в середине XIX века – проблема четырёх красок.
- 8. Немного из истории Среди работ первой половины XX века непосредственно относящихся к теории графов или существенно
- 9. Немного из истории Важнейшим событием для теории графов этого времени было появление в 1936 году монографии
- 10. Появились не только монографии К.Бержа «Теория конечных графов и её применение», 1962 (1958, Париж); О.Оре «Теория
- 11. На первый план выдвигаются рассуждения и построения дискретно-комбинаторного характера. Также резко возросло количество задач, сводящихся графам.
- 12. Таким образом, теория графов стала одной из существенных частей математического аппарата кибернетики, языком дискретной математики. Через
- 13. Задача о Кёнигсбергских мостах Как уже говорилось выше, основы теории графов как математической науки заложил в
- 14. В итоге Эйлер доказал общее утверждение: для того чтобы обойти все рёбра графа по одному разу
- 15. Возможно, многим подобного рода задачи знакомы ещё по журналам «Мурзилка», «Весёлые картинки» и др. Там предлагалось
- 16. В 1859 г. английский математик Уильям Гамильтон выпустил в продажу головоломку. Она представляла собой деревянный додекаэдр
- 17. Если поставить проволочный додекаэдр на плоскость, а затем поднести источник света к центру его верхней грани
- 18. В трёх избушках жили трое друзей. Около их домиков находилось три колодца: один с солёной водой,
- 19. Второй граф, с шестью вершинами и девятью рёбрами (рис.14), носит название «домики - колодцы». Оно произошло
- 20. Плоские графы обладают многими интересными свойствами. Так, Эйлер обнаружил простую связь между количеством вершин (B), количеством
- 21. Во многих случаях применения графов рёбра, соединяющие вершины, имеют чётко выраженное направление. Так на графах генеалогических
- 22. Графы, в которых все рёбра имеют направление, называются орграфами. На них удобно рассматривать различные транспортные задачи.
- 23. Если граф дорог боле сложен, то найти решение уже не легко. Были придуманы алгоритмы, позволяющие с
- 24. Например, зная дату начала строительства и время выполнения каждой работы, можно выяснить, к какому сроку следует
- 25. Ориентированные графы Ориентированный граф - это граф, на ребрах которого обозначены разрешенные направления движения, проще говоря,
- 26. - ориентированный цикл - это замкнутый простой путь в ориентированном графе; - сильно связный ориентированный граф
- 27. Задача 2. В королевстве каждый город соединен с каждым дорогой. Может ли сумасшедший король ввесте на
- 28. Требуются, требуются, требуются... Представим себе, что организуется географическая экспедиция на острова Тихого океана. В её состав
- 29. Мы рассмотрели специфический граф. Его вершины распадаются на два множества, такие, что вершины одного и того
- 30. Каждая фраза русского языка членится на составляющие. Мелкие составляющие входят в более крупные. Такое членение фразы
- 31. Рассмотрим еще одно дерево составляющих на примере предложения: «Важные лингвистические открытия нередко незаслуженно отвергались». Выделим сначала
- 32. Между словами, образующими правильную русскую фразу, существуют различные лингвистические отношения. Указать явным образом эти отношения —
- 33. Союз (и) можно здесь рассматривать как ритмическую вставку. Обратим внимание на то, что стрелки этого графа
- 34. Математическое свойство «древесности» трудно совместить с его синтаксической структурой, в том смысле, что дерево подчинения (это
- 35. А синтаксическое дерево подчинения называют расположенным относительно направляющей прямой, если при проекции на эту прямую никакие
- 36. С интуитивной точки зрения, решение вопроса о том, проста фраза или тяжеловесна, не составляет труда. Мы
- 38. Теперь давайте определим, как фразы одного писателя или поэта отличаются от других. А точнее, при анализе
- 39. Пушкинский текст в основном состоит из предложений, в которых не более 11 слов, а рисунки этих
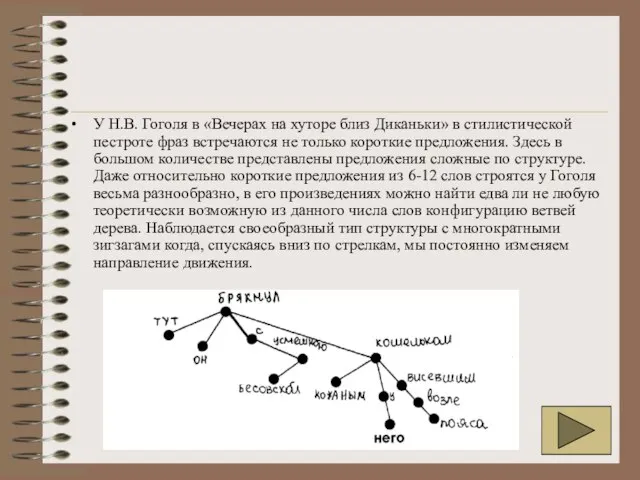
- 40. У Н.В. Гоголя в «Вечерах на хуторе близ Диканьки» в стилистической пестроте фраз встречаются не только
- 41. Сравнив прозу Л.Н. Толстого и Ф.М. Достоевского, можно отметить, что стилю обоих писателей присущи деревья достаточно
- 42. А теперь выясним, по какому принципу лингвисты поводят анализ художественного текста. И.П. Севбо привел семь таких
- 43. Как видите, с помощью графов, зная особенности стиля того или иного писателя, можно определить, кому принадлежит
- 44. Мы часто читаем произведения, переведенные с иностранного языка, но никогда не задумываемся над тем, насколько точен
- 45. 1. В. Шекспир. That time of year thou mayst in me be hold When yellow leaves,
- 46. 3. В. Брюсов. То время года видишь ты во мне, Когда, желтея, листья стали редки, И
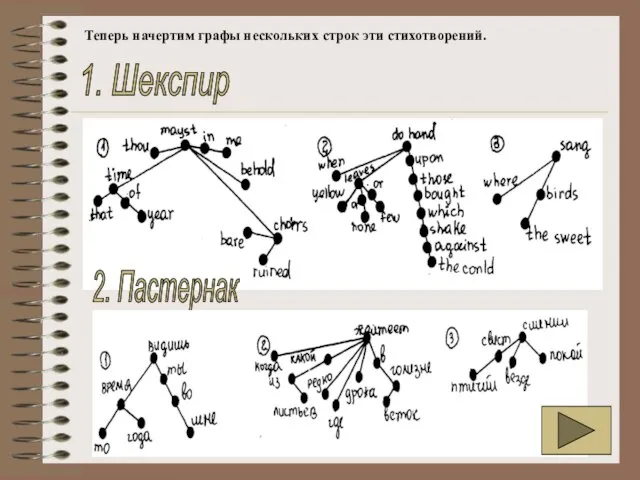
- 47. Теперь начертим графы нескольких строк эти стихотворений. 1. Шекспир 2. Пастернак
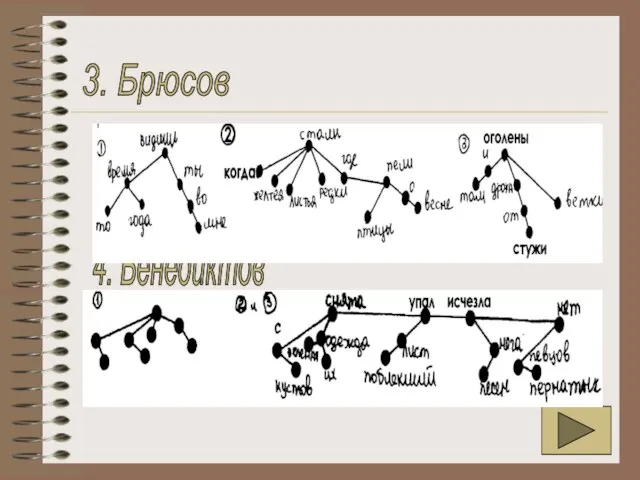
- 48. 3. Брюсов 4. Бенедиктов
- 49. Для анализа возьмём 5 и б строки, так как их перевод более точен по тексту и
- 50. А теперь наложим графы текстов перевода на граф оригинала. После наложения, щёлкните мышью
- 51. Анализируя графы с помощью признаков Севбо, я выяснил, что для текста Шекспира, в плане перевода, более
- 52. Заключение В этой презентации мы познакомились с различными сведения о графах, начиная с определения и простейших
- 53. Список источников: Энциклопедия для детей, том 11 Математика, Москва, «Аванта+», 1998 год. Математика. Еженедельное учебно-методическое приложение
- 54. Оре Ойстин «Теория графов», 1980 Уилсон Р. «Введение в теорию графов», 1977 Зыков Л.А. «Основа теории
- 56. Скачать презентацию
Слайд 2Цели и задачи проекта
Проиллюстрировать применение математики на практике
Показать связь с другими областями
Цели и задачи проекта
Проиллюстрировать применение математики на практике
Показать связь с другими областями

Познакомить с историческими сведениями
Подчеркнуть эстетические аспекты изучаемых вопросов
Слайд 4Понятие графов
Всем известно, что слово «граф» означает дворянский титул, например
Понятие графов
Всем известно, что слово «граф» означает дворянский титул, например

На рис.1 изображён граф хорошо известный москвичам. Это схема московского метро: вершины - конечные станции и станции пересадок, рёбра пути, соединяющие эти станции. На рис.2 вы видите ещё один граф – часть генеалогического дерева графа Льва Николаевича Толстого. Здесь вершины – предки писателя, а рёбра показывают родственные связи между ними.
Слайд 5Немного из истории
Появление теории графов как математической дисциплины, все единодушно относят к
Немного из истории
Появление теории графов как математической дисциплины, все единодушно относят к

Слайд 6Примерно в середине XIX века немецкий физик Г. Кирхгоф (1824-1871, иностранный член-корреспондент
Примерно в середине XIX века немецкий физик Г. Кирхгоф (1824-1871, иностранный член-корреспондент

Немного из истории
Слайд 7Немного из истории
Ещё одна проблема была сформулирована в середине XIX века
Немного из истории
Ещё одна проблема была сформулирована в середине XIX века

По-видимому, постановкой этой проблемы мы обязаны немецкому математику А.Мёбиусу (1799-1868, устное сообщение на лекциях в 1840 году). Известно также, что проблему пытались решить и другие известные математики, например, А.Де Морган, А.Кэли, причём последний в 1878 году сообщил, что не может её решить, и опубликовал формулировку этой проблемы в трудах Лондонского Королевского общества.
Слайд 8Немного из истории
Среди работ первой половины XX века непосредственно относящихся к
Немного из истории
Среди работ первой половины XX века непосредственно относящихся к

Критерий планарности графа доказали независимо друг от друга академик Российской Академии наук Л.С.Понтрягин в 1927 году и польский математик К.Куратовский в 1930 году (понятия планарного и плоского графа будут введены ниже).
Немецкий математик Д.Пойя предложил метод производящих функций, позволяющих решать задачи подсчёта графов, Встречающихся в различных областях науки.
Метод чередующихся цепей, идея которого восходит ещё к Е.Эгевари и который под названием «венгерского метода» и теперь успешно применяется в некоторых разделах теоретической и прикладной математики.
Слайд 9Немного из истории
Важнейшим событием для теории графов этого времени было появление
Немного из истории
Важнейшим событием для теории графов этого времени было появление

1948 году в «Успехах математических наук» опубликована работа «О некоторых математических вопросов теории электрических цепей», в которой успешно использованы графы. Автор этой работы ныне член-корреспондент Российской Академии наук Л.Д. Кудрявцев.
Вторая половина XX века с точки зрения развития графов существенно отличается от первой его половины. Во-первых, теория графов была признана математиками как самостоятельная математическая дисциплина.
Слайд 10Появились не только монографии К.Бержа «Теория конечных графов и её применение», 1962
Появились не только монографии К.Бержа «Теория конечных графов и её применение», 1962

Во-вторых положение сильно изменилось с связи с появлением малогабаритными, быстродействующими и надёжными ЭВМ, бурным развитием математической логики, машинной математике, автоматики, кибернетики, теории информации,
Немного из истории
математической экономики, теории игр исследования операций математической лингвистики и других областей, где, в отличии от классического анализа непрерывных величин.
Слайд 11На первый план выдвигаются рассуждения и построения дискретно-комбинаторного характера. Также резко возросло
На первый план выдвигаются рассуждения и построения дискретно-комбинаторного характера. Также резко возросло

Графами можно изображать, например, схемы дорог, коммуникаций, электрических цепей, молекул химических соединений, связей между людьми или группами людей. В терминах теории графов формируется большинство задач, связанных с дискретными объектами. Такие задачи возникают при проектировании интегральных схем и схем управления,
Немного из истории
блок-схем программ, в экономике, статистике, биологии, в теории расписаний, дискретной оптимизации других областей.
Слайд 12 Таким образом, теория графов стала одной из существенных частей математического аппарата
Таким образом, теория графов стала одной из существенных частей математического аппарата

Всё это привело к тому, что теория графов появилась в учебных программах наших университетов и технических вузах. И, наверно, пришло время ввести популярно изложенную теорию графов в учебные программы средних школ. Например, в США и многих других странах это сделали несколько десятков лет назад.
Немного из истории
Слайд 13Задача о Кёнигсбергских
мостах
Как уже говорилось выше, основы теории графов как
Задача о Кёнигсбергских
мостах
Как уже говорилось выше, основы теории графов как

Бывший Кёнигсберг(ныне Калининград)расположен на реке Прегель. В пределах города река омывает 2 острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены. Кёнигсберцы предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причём на каждом мосту следовало побывать только 1 раз.
Прогуляться по городским мостам предложили и Эйлеру. После безуспешной попытки совершить нужный обход он начертил упрощённую схему мостов. Получился граф, вершины которого–части города, а рёбра–мосты(рис.4).
Слайд 14 В итоге Эйлер доказал общее утверждение: для того чтобы обойти все
В итоге Эйлер доказал общее утверждение: для того чтобы обойти все

1) из любой вершины графа должен существовать путь по его рёбрам в любую другую вершину (графы, удовлетворяющие этому требованию, называют связными);
из каждой вершины должно выходить чётное количество рёбер.
2) Замкнутый путь, проходящий по одному разу по всем рёбрам графа, называют с тех пор эйлеровым циклом.
Если отбросить условие возвращения в исходную вершину, то можно допустить наличие двух вершин, из которых выходит нечётное количество рёбер. В этом случае начинать движение следует с одной из этих двух вершин, а заканчивать - в другой.
Слайд 15 Возможно, многим подобного рода задачи знакомы ещё по журналам «Мурзилка», «Весёлые
Возможно, многим подобного рода задачи знакомы ещё по журналам «Мурзилка», «Весёлые

А как же обстоит дело с кёнигсбергскими мостами? Здесь при каждой из четырёх вершин нечётное число рёбер, так что нет не только эйлерова цикла, но и пути из одной вершины в другую, проходящего по всем рёбрам графа.
рис.5
рис.4
Слайд 16 В 1859 г. английский математик Уильям Гамильтон выпустил в продажу головоломку.
В 1859 г. английский математик Уильям Гамильтон выпустил в продажу головоломку.

Игрушка не имела такой популярности, какой ещё недавно пользовался «кубик Рубика», но оставила след в математике. Замкнутый путь по рёбрам графа, проходящий по одному разу через все вершины, называют гамильтоновым циклом. В отличие от эйлерова цикла условия существования на произвольном графе гамильтонова цикла до сих пор не установлены.
Графы изоморфные и плоские
Слайд 17 Если поставить проволочный додекаэдр на плоскость, а затем поднести источник света
Если поставить проволочный додекаэдр на плоскость, а затем поднести источник света

Из опытов с проекцией видно, что свойства графов не меняются с изменением положения его вершин, не зависят от того, какими линиями они соединены. Два графа, изображённых на рис.9, в этом смысле одинаковы: у них одинаковое число вершин и если две вершины одного графа соединены ребром, то вершины второго графа, имеющие те же номера, тоже соединены ребром. Это замечание более строго формулируется так: да графа называются изоморфными (от греческого «изос» - равный, «морфе» - вид, форма), если между их вершинами можно установить взаимно однозначное соответствие, при котором вершинам, соединенным ребром, соответствуют вершины, также соединённые ребром.
Слайд 18В трёх избушках жили трое друзей. Около их домиков находилось три колодца:
В трёх избушках жили трое друзей. Около их домиков находилось три колодца:

Задача "Домики-колодцы"
рис.13
Мы знаем, что у изоморфных графов некоторых ребра пересекаются. А всегда ли граф можно изобразить на плоскости так, чтобы его рёбра не пересекались? Оказывается, нет. Графы, для которых это возможно называются плоскими.
Давайте рассмотрим задачу с плоскими графами
Слайд 19 Второй граф, с шестью вершинами и девятью рёбрами (рис.14), носит название
Второй граф, с шестью вершинами и девятью рёбрами (рис.14), носит название

Польский математик Казимеж Куратовский установил, что никаких принципиально иных не плоских графов не существует. Точнее, если граф не укладывается на плоскость, то в нём «сидит» по крайней мере, один из этих двух графов (полный граф с пятью вершинами или «домики – колодцы»), быть может, с дополнительными вершинами на рёбрах.
рис. 14
Слайд 20Плоские графы обладают многими интересными свойствами. Так, Эйлер обнаружил простую связь между
Плоские графы обладают многими интересными свойствами. Так, Эйлер обнаружил простую связь между

В – P + Г = 2
Если вспомнить, как с помощью лампочки плоский граф, изоморфный графу, состоящему из вершин и рёбер выпуклого многогранника, то легко понять, что эта формула верна для любого выпуклого многогранника. Этот факт, как недавно выяснилось, был известен ещё Рене Декарту.
Слайд 21Во многих случаях применения графов рёбра, соединяющие вершины, имеют чётко выраженное направление.
Во многих случаях применения графов рёбра, соединяющие вершины, имеют чётко выраженное направление.

Графом является и система улиц города. Его вершины – площади или перекрёстки, а рёбра – улицы. В больших городах на некоторых улицах устанавливается одностороннее движение. Естественно, что такой граф должен иметь направленные рёбра. Тогда улицы с двухсторонним движением можно обозначить парами рёбер с противоположным направлением.
Направленные графы
Слайд 22 Графы, в которых все рёбра имеют направление, называются орграфами. На них
Графы, в которых все рёбра имеют направление, называются орграфами. На них

Как видим, хотя из A может выезжать в час 7 тыс. машин, но въехать в B могут только 4 тыс. из них. Несложно проверить, что 4 тыс. машин в час остальные дороги в состоянии пропустить.
С другой стороны, из B в A могут выехать 3 тыс. машин в час, однако въехать в A смогут лишь 2 тыс. Поток в 2 тыс. машин из B в A остальные дороги, как нетрудно убедиться, также смогут пропустить.
Орграфы
Слайд 23 Если граф дорог боле сложен, то найти решение уже не легко.
Если граф дорог боле сложен, то найти решение уже не легко.

Вот ещё одно применение орграфа. При составлении больших проектов, содержащих различные виды работ, часто возникает ситуация, когда ту или иную работу можно начать лишь по окончании других. Так, при строительстве дома нельзя приступить к отделочным работам, пока не возведены стены, и нельзя возводить стены, до укладки фундамента. Последовательность работ изображается в виде орграфа (рис. 17). Здесь вершины – производимые работы (с указанием их продолжительности), а стрелки указывают, какие из них могут выполняться только по окончании предыдущих. Такие орграфы называются сетевыми графиками. Они применяются при планировании деятельности предприятия.
Слайд 24Например, зная дату начала строительства и время выполнения каждой работы, можно выяснить,
Например, зная дату начала строительства и время выполнения каждой работы, можно выяснить,

Сетевые графики используют не только строители, но и конструкторы машин с большим количеством узлов и деталей, диспетчеры железных дорог и многие другие специалисты.
Слайд 25Ориентированные графы
Ориентированный граф - это граф, на ребрах которого обозначены разрешенные
Ориентированные графы
Ориентированный граф - это граф, на ребрах которого обозначены разрешенные

Слайд 26- ориентированный цикл - это замкнутый простой путь в ориентированном графе;
- сильно
- ориентированный цикл - это замкнутый простой путь в ориентированном графе; - сильно

В задачах на ориентированный граф обычно упоминаются всякие реки, потоки или дороги с односторонним движением. Иногда - односторонние отношения между людьми ;-)
Задача 1. Барон Мюнхаузен, прилетев с Луны, рассказал, что в каждое лунное море впадает пять рек, а из каждого лунного моря вытекает шесть рек. Докажите, что он говорит неправду.
Решение: Пусть на Луне N морей. Посчитаем реки двумя способами: по тому, откуда они вытекают, и по тому, куда они впадают. Первым способом получается, что рек 6N, а вторым - что 5N. Противоречие, ч.т.д.
(!) Аналогичным рассуждением доказывается, что в ориентированном графе сумма входящих степеней равна сумме исходящих, так как каждая из них равна числу ребер. Действительно, у каждого ориентированного ребра одно начало и один конец (сравните с утверждением про сумму степеней вершин обычного графа!).
Решение задач с помощью ориентированных графов
Слайд 27Задача 2. В королевстве каждый город соединен с каждым дорогой. Может ли
Задача 2. В королевстве каждый город соединен с каждым дорогой. Может ли

Интересно... в каждом примере все ребра идут именно слева направо (особенно легко это получается, если каждый следующий пример строить как расширение предыдущего!). Так давайте всегда проводить все ребра слева направо (при этом избегая рисовать вершины в точности друг над другом). Тогда, выехав из любого города, мы будем оказываться все правее и правее, и никогда не вернемся в исходную точку. Значит, можно.
Можно формализовать это и без геометрических соображений о том, как нарисован граф: занумеровать все вершины и ставить все стрелки от меньшего номера к большему.
Замечание. В построенном графе каждая вершина - отдельная компонента сильной связности.
Слайд 28Требуются, требуются,
требуются...
Представим себе, что организуется географическая экспедиция на острова Тихого океана.
Требуются, требуются,
требуются...
Представим себе, что организуется географическая экспедиция на острова Тихого океана.

Нарисуем граф, у которого две группы вершин: десять соответствуют претендентам и семь – должностям. Рёбрами соединим вершины претендентов с вершинами их специальностей (рис.18).
Казалось бы, всё в порядке, на каждое место есть кандидат. Однако впечатление это обманчиво. Посмотрите: на должность врача имеется лишь один претендент (№3), разумеется, он её и займет. Но тогда на три места географов останутся только 2 претендента. Таким образом, из этой группы желающих не удастся собрать команду экспедиции.
Слайд 29Мы рассмотрели специфический граф. Его вершины распадаются на два множества, такие, что
Мы рассмотрели специфический граф. Его вершины распадаются на два множества, такие, что

Теперь заглянем на биржу труда. Сюда пришли семь человек. Им предложили десять рабочих мест по тем специальностям, которыми они владеют. Снова нарисуем двудольный граф соответствия людей и профессий (рис.19). Этот граф похож на предыдущий, только люди и вакансии поменялись местами. Смогут ли все семеро получить работу по специальности?
Слайд 30Каждая фраза русского языка членится на составляющие. Мелкие составляющие входят в более
Каждая фраза русского языка членится на составляющие. Мелкие составляющие входят в более

«(Все1 это2) (сильно3 (поколебало4 (мою5 (авторскую6 уверенность7))))»
В сущности кавычки здесь также могут играть роль скобок, выделяющих максимальную составляющую. В число составляющих мы будем включать и отдельные слова, которые обозначим Х, L. В рассмотренном примере мы выделим следующие составляющие:
L1= (х1, х2, x3, х4, х5, х6, х7)
L2 = (х1, x2)
L3 = (х3, х4, х5, х6, х7)
L4 = (х3, х4, х5, x6, х7)
L5 = (х5, х6, х7)
L6 = (х6, х7)
Граф составляющий
Изобразим данное отношение с помощью графов:
Этот граф является несимметричным деревом, которое наиболее ветвится вправо.
Слайд 31Рассмотрим еще одно дерево составляющих на примере предложения: «Важные лингвистические открытия нередко
Рассмотрим еще одно дерево составляющих на примере предложения: «Важные лингвистические открытия нередко
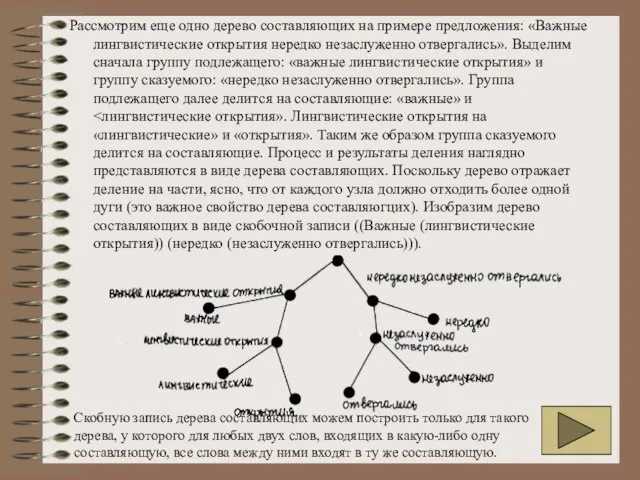
Скобную запись дерева составляющих можем построить только для такого дерева, у которого для любых двух слов, входящих в какую-либо одну составляющую, все слова между ними входят в ту же составляющую.
Слайд 32Между словами, образующими правильную русскую фразу, существуют различные лингвистические отношения. Указать явным
Между словами, образующими правильную русскую фразу, существуют различные лингвистические отношения. Указать явным

Обозначим его символом ( )Оно является асимметричным отношением. Согласно сложившейся традиции, считается, что управление идет от определяемого к определению, от сказуемого к подлежащему, от предлога к существительному, от глагола к прямому дополнению, от глагола к предлогу.
Рассмотрим, как расставляются управления на конкретной фразе с нумерацией слов:
«И1 сатана2 привстав3 с4 весельем5 на6 лике7 лобзанием8 своим9 насквозь10 прожег11 уста12 в13 предательскую14 ночь15 лобзавшие16 Христа17».
Граф управления
Слайд 33Союз (и) можно здесь рассматривать как ритмическую вставку. Обратим внимание на то,
Союз (и) можно здесь рассматривать как ритмическую вставку. Обратим внимание на то,

Одним из типов отношений между вхождением слов во фразу является согласование. Под согласованием понимается наличие явно выраженных общих грамматических признаков, связывающих данную пару слов в коллектив. Например: согласование прилагательного и существительного по роду, числу и падежу (обозначим δ). В предыдущей фразе мы имеем, например: соотношения ХI4δХ15 и Х15δХI4δ т.е. они асимметричны.
Слайд 34Математическое свойство «древесности» трудно совместить с его синтаксической структурой, в том смысле,
Математическое свойство «древесности» трудно совместить с его синтаксической структурой, в том смысле,
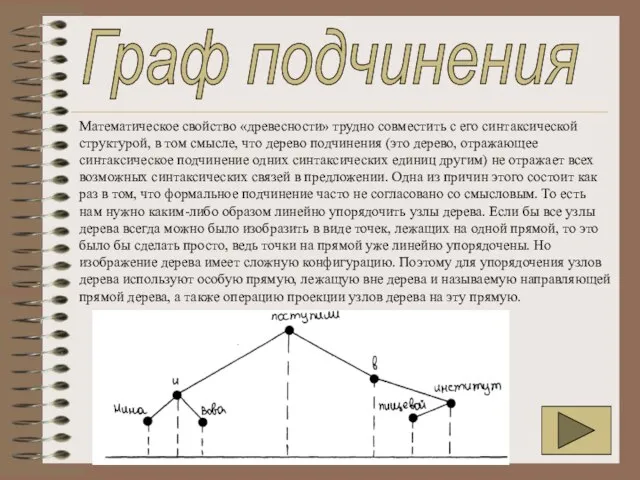
Граф подчинения
Слайд 35А синтаксическое дерево подчинения называют расположенным относительно направляющей прямой, если при проекции
А синтаксическое дерево подчинения называют расположенным относительно направляющей прямой, если при проекции

Но не следует думать, что проективность сама по себе всегда обеспечивает правильный порядок слов. Речь идет о поэзии, свободной от многих форм обычного языка. Благодаря непроективным структурам достигается возвышенность приподнятого стиля, например, в стихотворении А.С. Пушкина.
Слайд 36С интуитивной точки зрения, решение вопроса о том, проста фраза или тяжеловесна,
С интуитивной точки зрения, решение вопроса о том, проста фраза или тяжеловесна,

Теория громоздкости
Слайд 38Теперь давайте определим, как фразы одного писателя или поэта отличаются от других.
Теперь давайте определим, как фразы одного писателя или поэта отличаются от других.
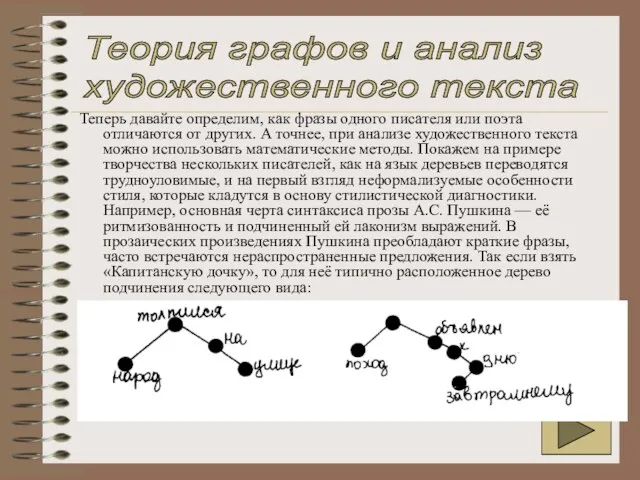
Теория графов и анализ
художественного текста
Слайд 39Пушкинский текст в основном состоит из предложений, в которых не более 11
Пушкинский текст в основном состоит из предложений, в которых не более 11
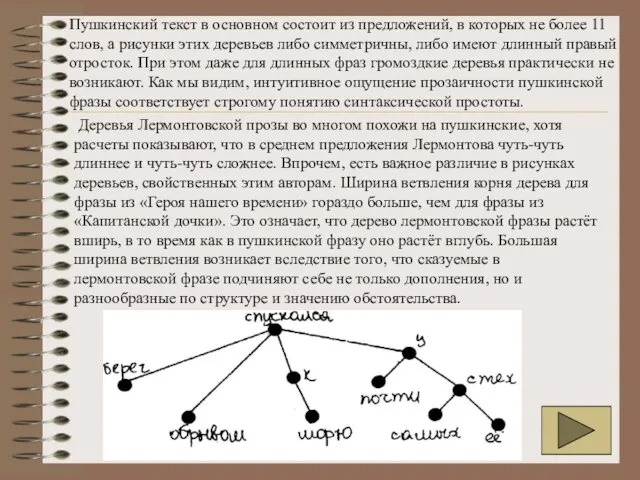
Деревья Лермонтовской прозы во многом похожи на пушкинские, хотя расчеты показывают, что в среднем предложения Лермонтова чуть-чуть длиннее и чуть-чуть сложнее. Впрочем, есть важное различие в рисунках деревьев, свойственных этим авторам. Ширина ветвления корня дерева для фразы из «Героя нашего времени» гораздо больше, чем для фразы из «Капитанской дочки». Это означает, что дерево лермонтовской фразы растёт вширь, в то время как в пушкинской фразу оно растёт вглубь. Большая ширина ветвления возникает вследствие того, что сказуемые в лермонтовской фразе подчиняют себе не только дополнения, но и разнообразные по структуре и значению обстоятельства.
Слайд 40У Н.В. Гоголя в «Вечерах на хуторе близ Диканьки» в стилистической пестроте
У Н.В. Гоголя в «Вечерах на хуторе близ Диканьки» в стилистической пестроте
Слайд 41Сравнив прозу Л.Н. Толстого и Ф.М. Достоевского, можно отметить, что стилю обоих
Сравнив прозу Л.Н. Толстого и Ф.М. Достоевского, можно отметить, что стилю обоих

Слайд 42А теперь выясним, по какому принципу лингвисты поводят анализ художественного текста. И.П.
А теперь выясним, по какому принципу лингвисты поводят анализ художественного текста. И.П.

Количество узлов дерева (т.е. количество слов во фразе)
Количество простых предложений в сложном (помечание стрелок, соответствующих связям между частями сложного предложения)
Число уровней в дереве (длина самого длинного из путей дерева)
Ширина ветвления корня (число узлов подчиненных корню)
Проведем эксперимент. Перед нами строки из произведения «Кавказский пленник» А.С. Пушкина и М.Ю. Лермонтова. Нам нужно определить, какой граф принадлежит Пушкину, а какой Лермонтову. Мы это сделаем с помощью Севбо.
Признаки И.Л. Севбо
Слайд 43Как видите, с помощью графов, зная особенности стиля того или иного писателя,
Как видите, с помощью графов, зная особенности стиля того или иного писателя,
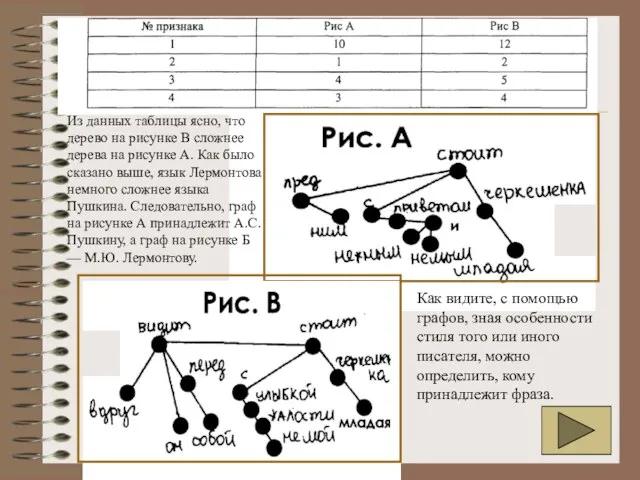
Из данных таблицы ясно, что дерево на рисунке В сложнее дерева на рисунке А. Как было сказано выше, язык Лермонтова немного сложнее языка Пушкина. Следовательно, граф на рисунке А принадлежит А.С. Пушкину, а граф на рисунке Б — М.Ю. Лермонтову.
Слайд 44 Мы часто читаем произведения, переведенные с иностранного языка, но никогда не
Мы часто читаем произведения, переведенные с иностранного языка, но никогда не

Графы и стилистика
переводов иностранных текстов
Слайд 451. В. Шекспир.
That time of year thou mayst in me be hold
When
1. В. Шекспир.
That time of year thou mayst in me be hold
When

Upon those boughs which shake against the cold
In me thou seest the twilight of such day
As after sunset fadeth in the west
Which by and by black night doth take away,
Death’s second self that seals up all the rest.
In my thou seest the glowing of such fire,
That on the ashes of his youth doth lie,
As the death-bed, whereon it must expire,
Consumed with that which it was nourished by.
This thou perciev’st, which makes thy love more strong,
To love that well, which thou must leave ere long.
2. Б. Пастернак.
То время года видишь ты во мне,
Когда из листьев редко, где какой,
Дрожа, желтеет в веток голизне,
А птичий свист везде сменил покой.
Во мне ты видишь бледный край
небес,
Где от заката памятка одна
И, постепенно взявши перевес,
Их отпечатывает темнота.
Во мне ты видишь то сгоранье дна,
Когда зола, что пламенем была,
Становится могилою огня,
А то, что грело, изошло дотла
И, это видя, помни: нет цены
Свиданьям, дни которых сочтены.
Слайд 463. В. Брюсов.
То время года видишь ты во мне,
Когда, желтея, листья стали
3. В. Брюсов.
То время года видишь ты во мне,
Когда, желтея, листья стали

И там, где птицы пели о весне,
Оголены , дрожа от стужи, ветки.
Во мне ты сумерки находишь дня,
Что гаснет после яркого заката;
Ночь тёмная, к покою всех клоня
(Двойник твой Смерть!), его влечет куда-то!
Во мне ты видишь отблески огней,
Лежавших в пепле юности своей;
Они окончат жизнь на том ложе.
Снедаемые тем, что их запекло,
И потому, что день ты любишь строже,
Спеши любить то, что почти прошло!
4. В. Бенедиктов.
Во мне перед собой ты видишь время снега,
С кустов зеленая одежда их снята,
Певцов пернатых нет, в оркестре пустота.
Поблёклый лист упал, исчезла песен нега -
Во мне перед собой ты видишь час ночлега,
На западе дрожит чуть светлая черта,
И всё густеет мрак, мрак — этот after ego
Тьмы смертной, вечной тьмы, недалека и та.
Во мне перед тобой дней прошлых лишь остаток,
Лишь искры над золой, а пламень прекращен,
Убитый тем, чем жил и чем питался он.
Люби ж меня сильней! Ты видишь: срок мой краток,
Ты потерять меня страшишься — миг лови!
Чем больше этот страх, тем больше дай любви!
Слайд 47Теперь начертим графы нескольких строк эти стихотворений.
1. Шекспир
2. Пастернак
Теперь начертим графы нескольких строк эти стихотворений.
1. Шекспир
2. Пастернак
Слайд 483. Брюсов
4. Бенедиктов
3. Брюсов
4. Бенедиктов
Слайд 49Для анализа возьмём 5 и б строки, так как их перевод более
Для анализа возьмём 5 и б строки, так как их перевод более
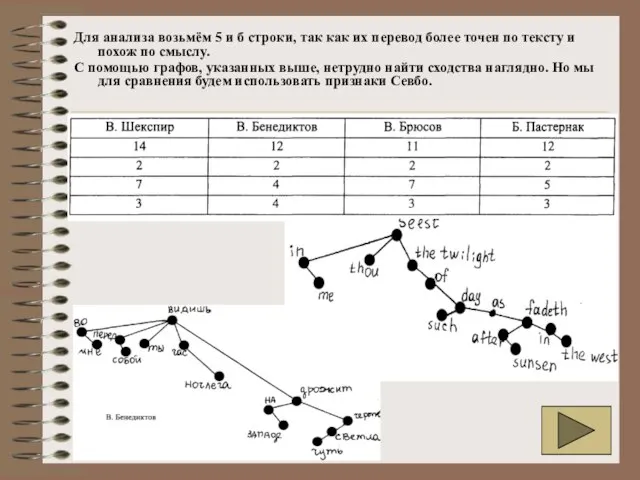
С помощью графов, указанных выше, нетрудно найти сходства наглядно. Но мы для сравнения будем использовать признаки Севбо.
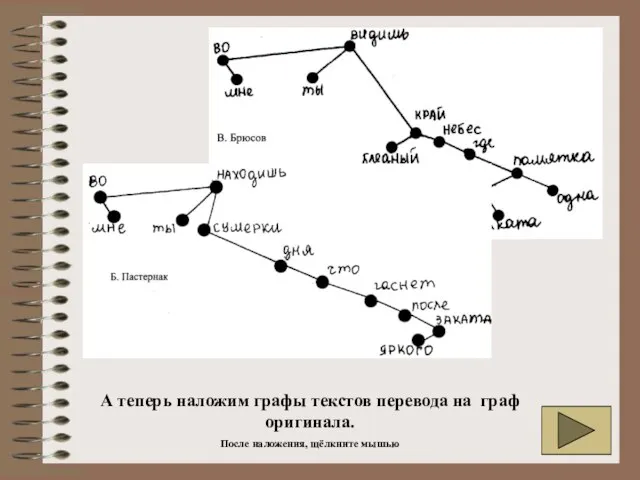
Слайд 50А теперь наложим графы текстов перевода на граф оригинала.
После наложения, щёлкните мышью
А теперь наложим графы текстов перевода на граф оригинала.
После наложения, щёлкните мышью
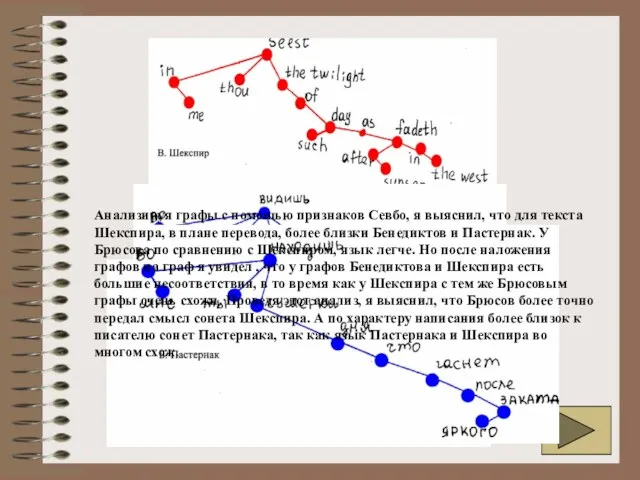
Слайд 51Анализируя графы с помощью признаков Севбо, я выяснил, что для текста Шекспира,
Анализируя графы с помощью признаков Севбо, я выяснил, что для текста Шекспира,
Слайд 52Заключение
В этой презентации мы познакомились с различными сведения о графах, начиная с
Заключение
В этой презентации мы познакомились с различными сведения о графах, начиная с

Слайд 53Список источников:
Энциклопедия для детей, том 11 Математика, Москва, «Аванта+», 1998 год.
Математика. Еженедельное
Список источников:
Энциклопедия для детей, том 11 Математика, Москва, «Аванта+», 1998 год.
Математика. Еженедельное

Оре Ойстин «Графы и их применение» М, 1965
Саркисян А.А., М.Ю. Колягин «Познакомьтесь с топологией» М.,1976
Липатов Е. П. «Теория графов и её применение», 1986
Берж К. «Теория графов и её применение», 1962
Верезина Л.Ю. «Графы и их применение», 1979
Слайд 54Оре Ойстин «Теория графов», 1980
Уилсон Р. «Введение в теорию графов», 1977
Зыков Л.А.
Оре Ойстин «Теория графов», 1980
Уилсон Р. «Введение в теорию графов», 1977
Зыков Л.А.

Крейдлин Г.Е. «Математика помогает лингвистике», 1994
Басанер Р. И Саити Т. «Конечные графы и сети» М, 1971
Шрейдер Ю.А. «Равенство, сходство, порядок» М, 1971
Сайт в Интернете
http://acadclasses.narod.ru/math/lectures.htm


 Sozdanie_Khrama_Gretsii_V_3D_Individualny_Proekt_Popovoy_E_9a
Sozdanie_Khrama_Gretsii_V_3D_Individualny_Proekt_Popovoy_E_9a Отношения в решении задач
Отношения в решении задач Национальная стандартизация
Национальная стандартизация Автоматизация звука Ц
Автоматизация звука Ц Презентация на тему Золотое сечение - божественная мера красоты (7 класс)
Презентация на тему Золотое сечение - божественная мера красоты (7 класс) лекція 2
лекція 2 Конденсаторы
Конденсаторы Аксаков Сергей Тимофеевич
Аксаков Сергей Тимофеевич Логические ошибки
Логические ошибки Каждый день улетают самолёты, Каждый час уезжают поезда Но, а я останусь с Иисусом Навсегда, навсегда, навсегда.
Каждый день улетают самолёты, Каждый час уезжают поезда Но, а я останусь с Иисусом Навсегда, навсегда, навсегда. Исследовательская деятельность как средство развития познавательной активности учащихся на уроках литературы
Исследовательская деятельность как средство развития познавательной активности учащихся на уроках литературы Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 1 г. Ершова Саратовской области» Мастер –
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 1 г. Ершова Саратовской области» Мастер – Приготовление сложной холодной кулинарной продукции в столовой при производственном предприятии на 120 посадочных мест
Приготовление сложной холодной кулинарной продукции в столовой при производственном предприятии на 120 посадочных мест Оборудование ОРУ
Оборудование ОРУ ТЕМА №2: ПОЗНАВАТЕЛЬНЫЕ ПРОЦЕССЫ
ТЕМА №2: ПОЗНАВАТЕЛЬНЫЕ ПРОЦЕССЫ Предотвращение
Предотвращение Популярно о криптографииОсновные понятия
Популярно о криптографииОсновные понятия КТОП Лабораторная работа №1
КТОП Лабораторная работа №1 Презентация квалификационной работы слушателя программы МBA Соловьевой В.В «Разработка системы этических документов как фактор р
Презентация квалификационной работы слушателя программы МBA Соловьевой В.В «Разработка системы этических документов как фактор р Клинический случай
Клинический случай Изобразительное искусство как способ влияния на эмоциональное и физическое состояние человека
Изобразительное искусство как способ влияния на эмоциональное и физическое состояние человека Презентация на тему Трагическая хроника атомной эпохи по отечественным и зарубежным публикациям
Презентация на тему Трагическая хроника атомной эпохи по отечественным и зарубежным публикациям Четырехугольники. Квадрат. Диагностическое домашнее задание
Четырехугольники. Квадрат. Диагностическое домашнее задание DEVELOPMENT PROSPECTS OF THE ALMATY METRO / Ppt-Presentation by Gleb K.Samoilov. – Almaty, 2016. – 47 p.
DEVELOPMENT PROSPECTS OF THE ALMATY METRO / Ppt-Presentation by Gleb K.Samoilov. – Almaty, 2016. – 47 p. Тест по теме «Устройства ПК»
Тест по теме «Устройства ПК» Проект участника РМЦ по ремонту оборудования резьбофрезерного полуавтомата модели
Проект участника РМЦ по ремонту оборудования резьбофрезерного полуавтомата модели Система стандартов«Интеграционная платформы информационных систем органов государственной власти» (ИП/ОГВ)
Система стандартов«Интеграционная платформы информационных систем органов государственной власти» (ИП/ОГВ) 1. Целые и рациональные числа. Математика (СПО 1 курс)
1. Целые и рациональные числа. Математика (СПО 1 курс)