Коллективные моды магнитного резонанса в спин-щелевых магнетиках

Гейзенберговский обмен и проблема основного состояния
антиферромагнетиков
H =Σ Ji,i+1 SiS i+1
H = Ji,i+1 Σ [SzjSzj+1+1/2(S+jS-j+1 + S-jS+ j+1 )]
S+i = Sxi+iSyi Si= Sxi-iSyi
Это – классическое основное состояние для J > 0
Но оно не является
cобственным
для гамильтониана
-
-

0
-1/4
-3/4
-E/NJ
-ln2+1/4 (H.Bethe, 1931)
=0
z
ξ
=
Цепочка спинов S=1/2 (анзац Бете)

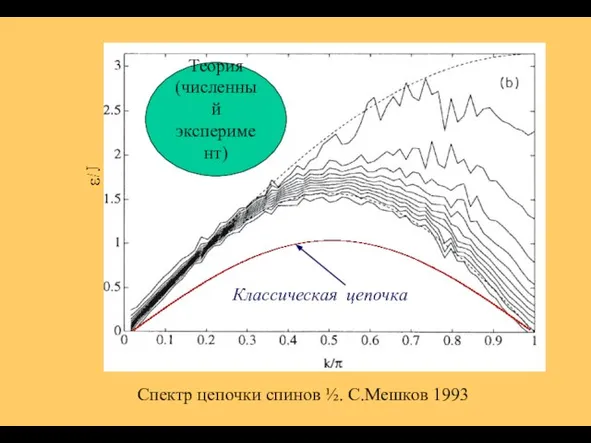
Спектр цепочки спинов ½. С.Мешков 1993
Классическая цепочка
Теория
(численный
эксперимент)

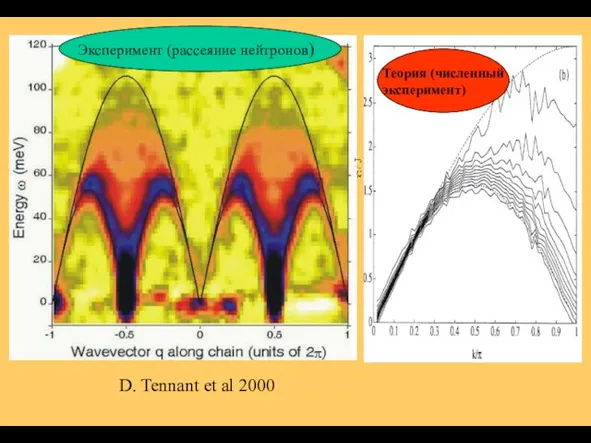
Спектр возбуждений
в KCuF3
D. Tennant et al 2000
Теория (численный
эксперимент)
Эксперимент (рассеяние нейтронов)

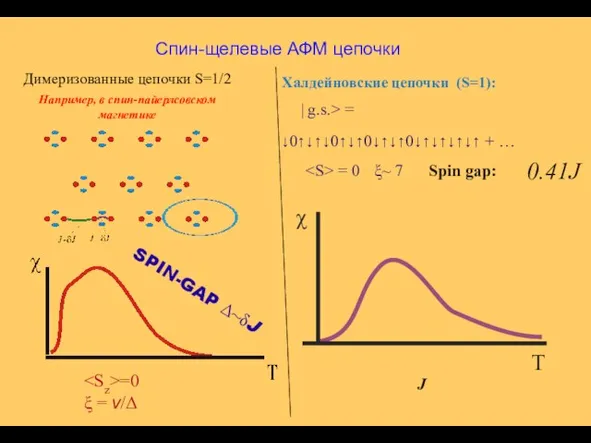
Димеризованные цепочки S=1/2
Например, в спин-пайерлсовском магнетике
Спин-щелевые АФМ цепочки
SPIN-GAP Δ~δJ
=0
ξ = v/Δ
Халдейновские цепочки (S=1):
| g.s.> =
↓0↑↓↑↓0↑↓↑0↓↑↓↑0↓↑↓↑↓↑↓↑ + …
= 0
ξ~ 7
0.41J
Spin gap:
χ
T
J

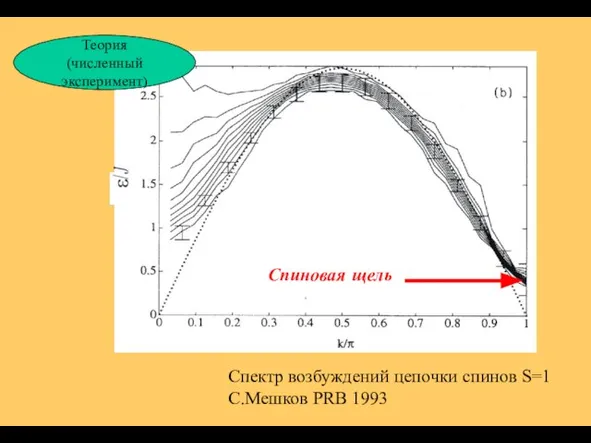
Спектр возбуждений цепочки спинов S=1
С.Мешков PRB 1993
Спиновая щель
Теория
(численный эксперимент)

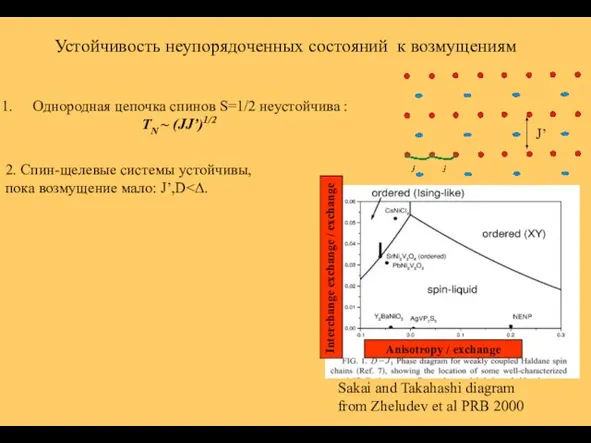
Устойчивость неупорядоченных состояний к возмущениям
Однородная цепочка спинов S=1/2 неустойчива :
TN ~ (JJ’)1/2
2. Спин-щелевые системы устойчивы,
пока возмущение мало: J’,D<Δ.
J’
Sakai and Takahashi diagram
from Zheludev et al PRB 2000
Interchange exchange / exchange
Anisotropy / exchange

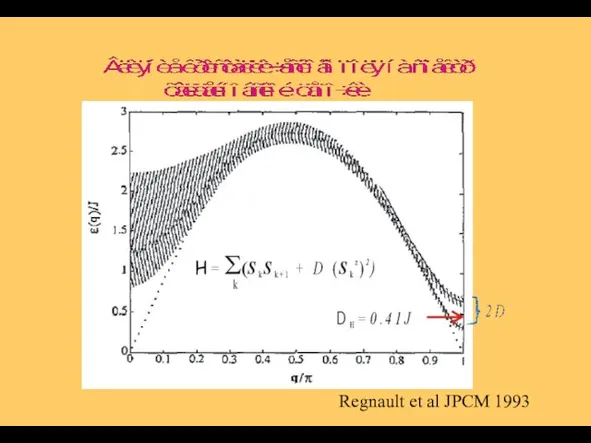
Regnault et al JPCM 1993

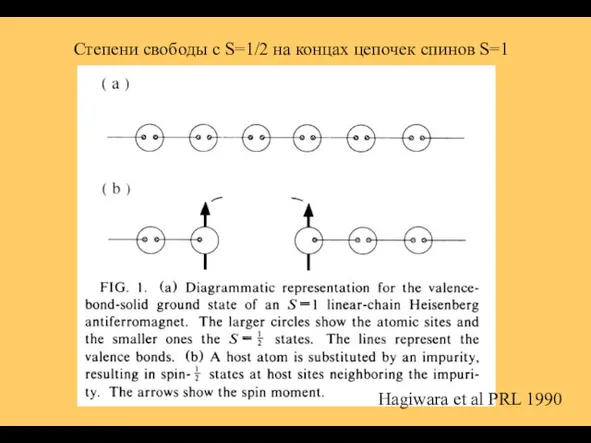
Степени свободы c S=1/2 на концах цепочек спинов S=1
Hagiwara et al PRL 1990

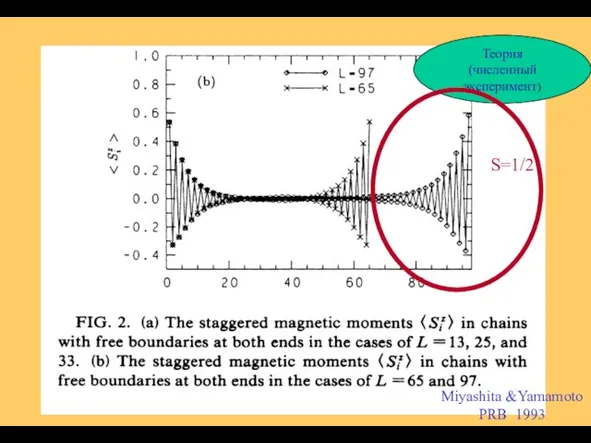
Miyashita &Yamamoto
PRB 1993
Теория
(численный эксперимент)
S=1/2

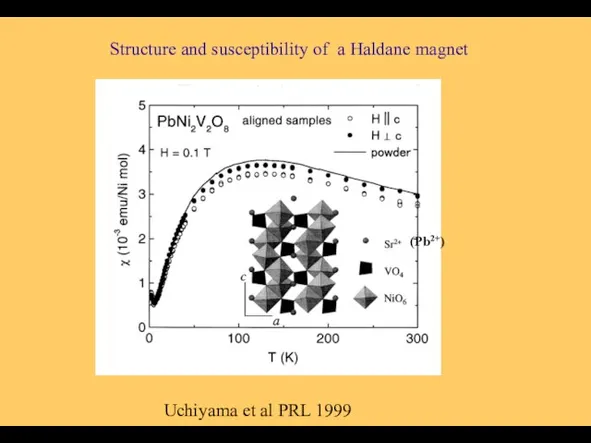
Structure and susceptibility of a Haldane magnet
Uchiyama et al PRL 1999
(Pb2+)

↑
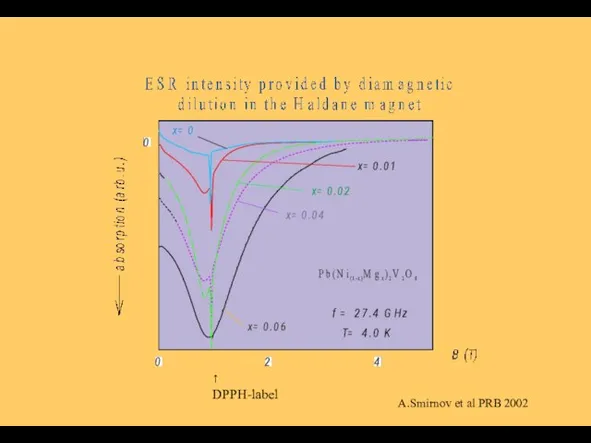
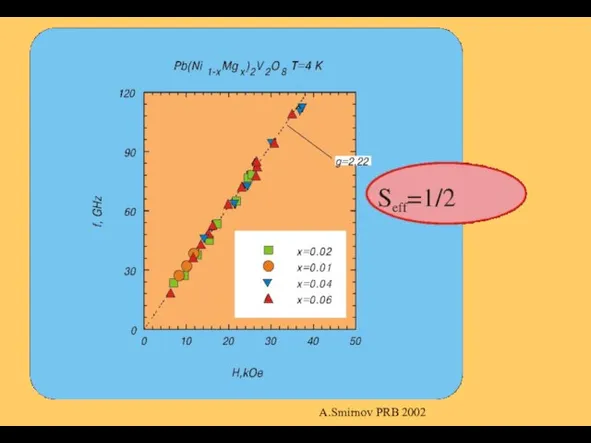
DPPH-label
A.Smirnov et al PRB 2002

A.Smirnov PRB 2002

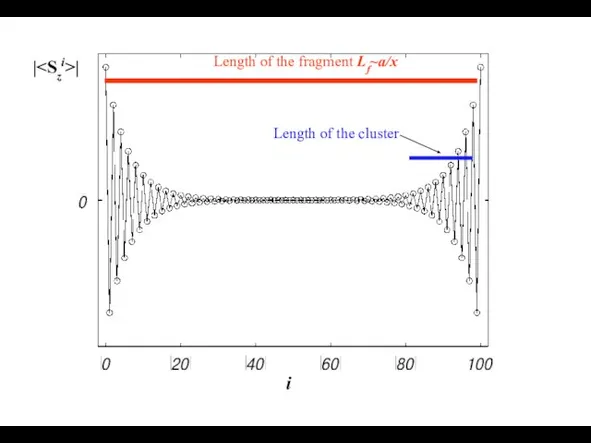
Length of the fragment Lf~a/x
Length of the cluster
|
|
i

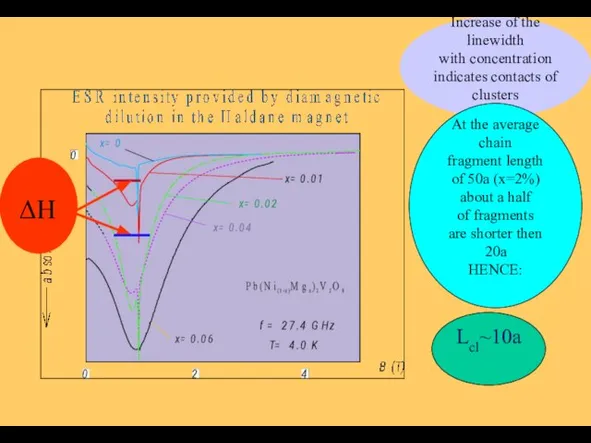
ΔH
Lcl~10a
Increase of the linewidth
with concentration
indicates contacts of clusters
At the average chain
fragment length
of 50a (x=2%)
about a half
of fragments
are shorter then 20a
HENCE:

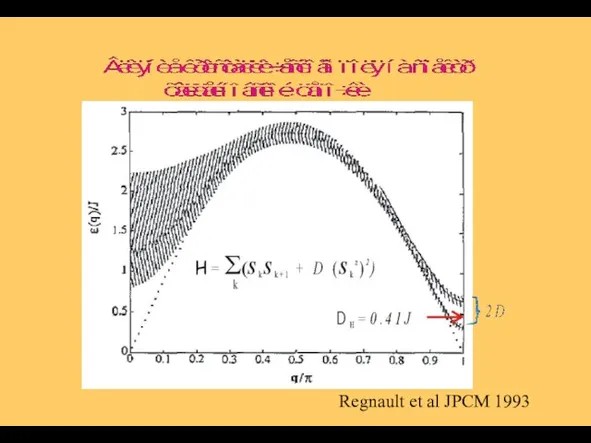
Regnault et al JPCM 1993

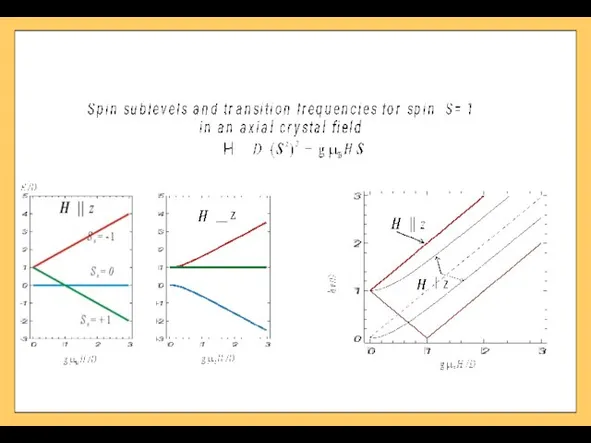
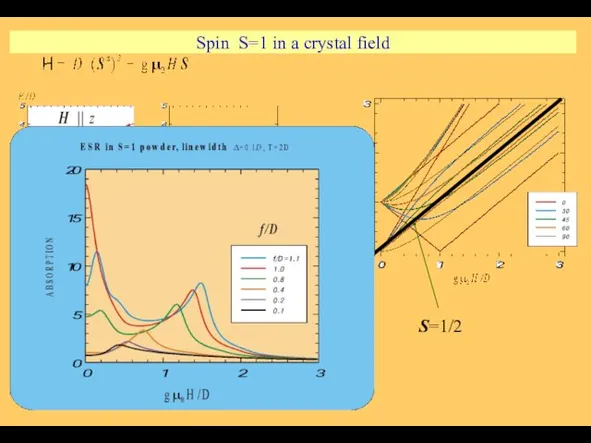
S=1/2
Spin S=1 in a crystal field

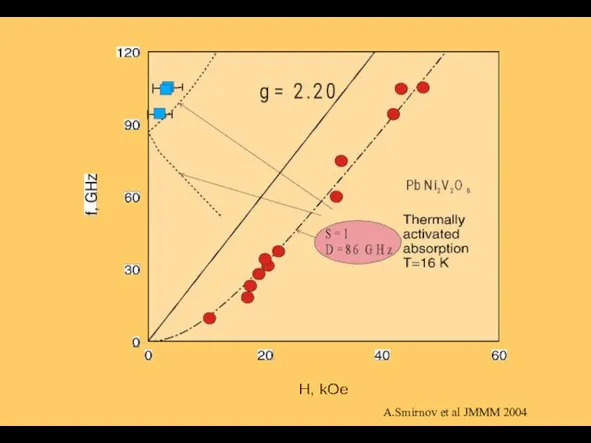
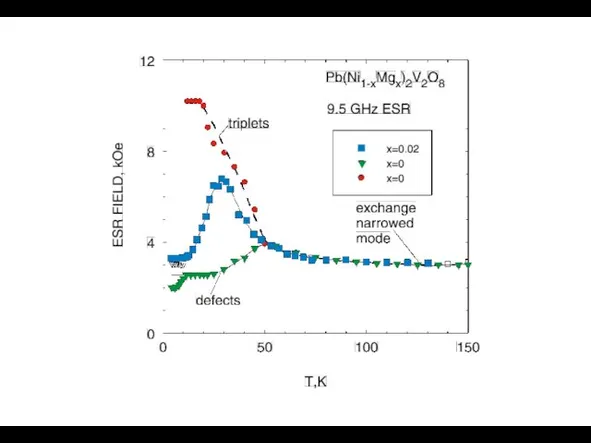
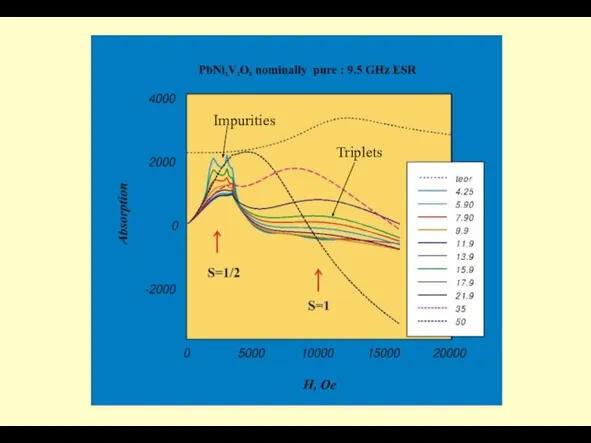
A.Smirnov et al JMMM 2004

Triplets
Impurities

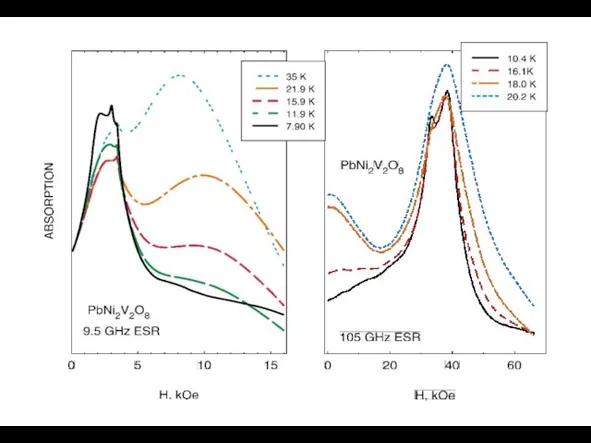
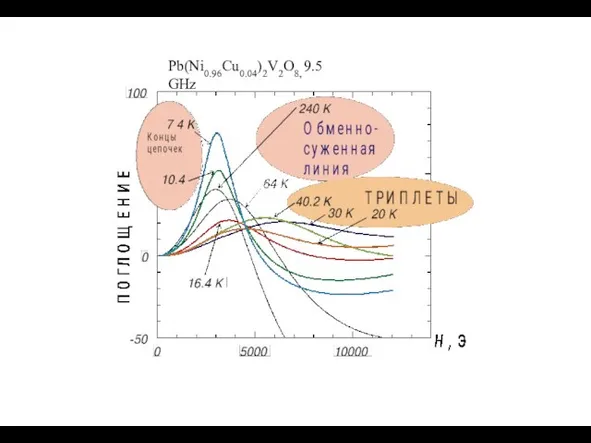
Pb(Ni0.96Cu0.04)2V2O8, 9.5 GHz

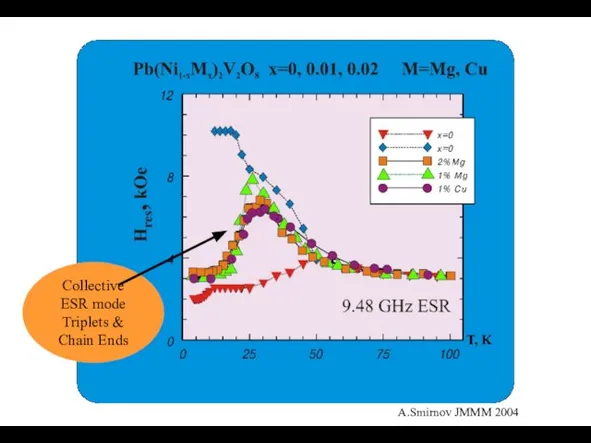
Collective ESR mode
Triplets & Chain Ends
A.Smirnov JMMM 2004

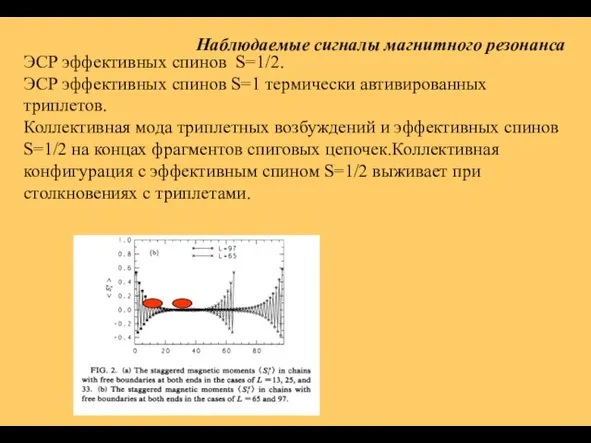
ЭСР эффективных спинов S=1/2.
ЭСР эффективных спинов S=1 термически автивированных триплетов.
Коллективная мода триплетных возбуждений и эффективных спинов S=1/2 на концах фрагментов спиговых цепочек.Коллективная конфигурация с эффективным спином S=1/2 выживает при столкновениях с триплетами.
Наблюдаемые сигналы магнитного резонанса

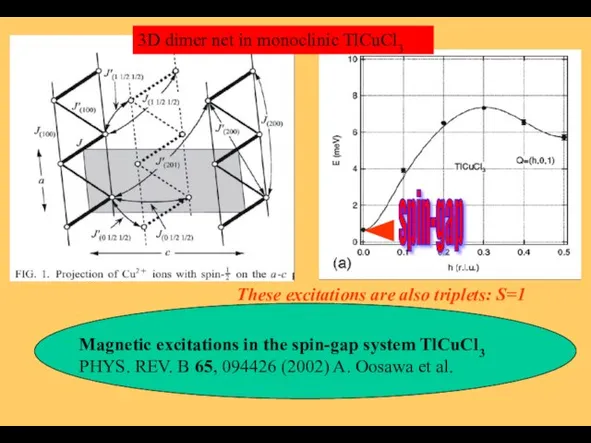
Magnetic excitations in the spin-gap system TlCuCl3
PHYS. REV. B 65, 094426 (2002) A. Oosawa et al.
spin-gap
3D dimer net in monoclinic TlCuCl3
These excitations are also triplets: S=1

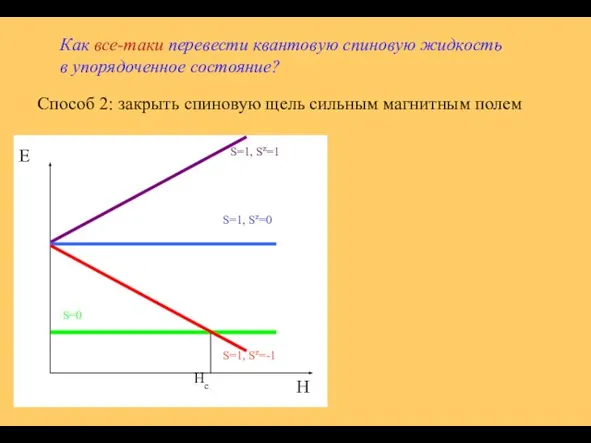
Как все-таки перевести квантовую спиновую жидкость
в упорядоченное состояние?
Способ 2: закрыть спиновую щель сильным магнитным полем

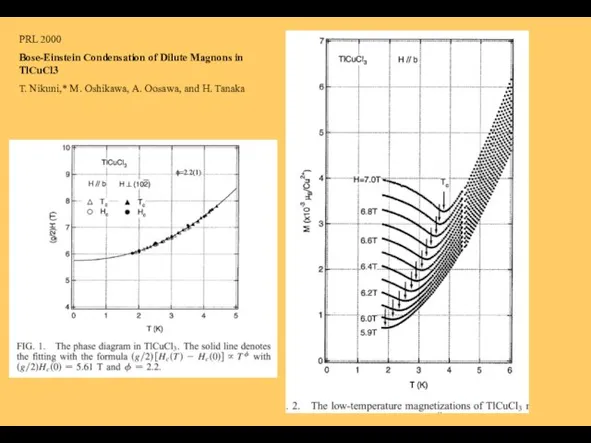
PRL 2000
Bose-Einstein Condensation of Dilute Magnons in TlCuCl3
T. Nikuni,* M. Oshikawa, A. Oosawa, and H. Tanaka

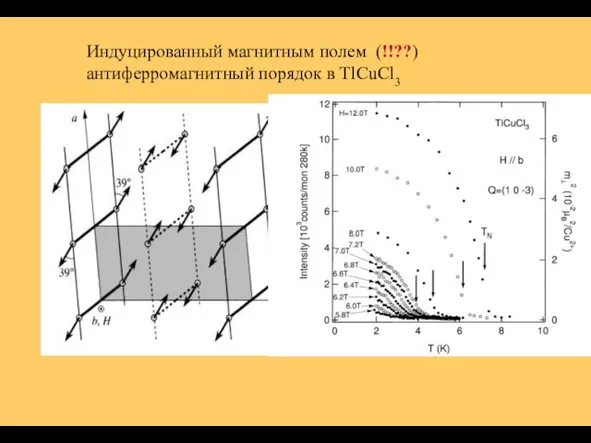
Индуцированный магнитным полем (!!??)
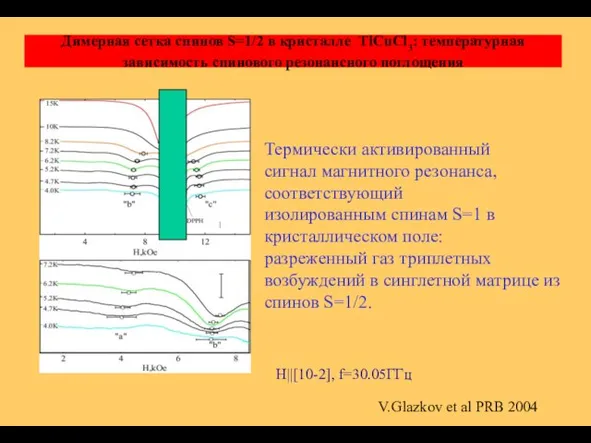
антиферромагнитный порядок в TlCuCl3

Димерная сетка спинов S=1/2 в кристалле TlCuCl3: температурная зависимость спинового резонансного поглощения
H||[10-2], f=30.05ГГц
V.Glazkov et al PRB 2004
Термически активированный
сигнал магнитного резонанса, соответствующий
изолированным спинам S=1 в кристаллическом поле:
разреженный газ триплетных возбуждений в синглетной матрице из спинов S=1/2.

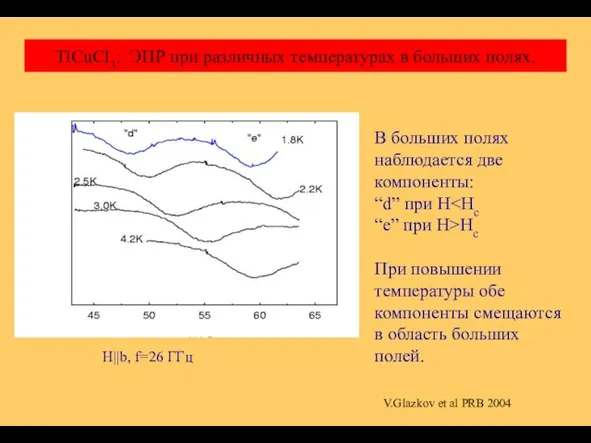
H||b, f=26 ГГц
В больших полях наблюдается две компоненты:
“d” при H
“e” при H>Hc
При повышении температуры обе компоненты смещаются в область больших полей.
TlCuCl3: ЭПР при различных температурах в больших полях.
V.Glazkov et al PRB 2004

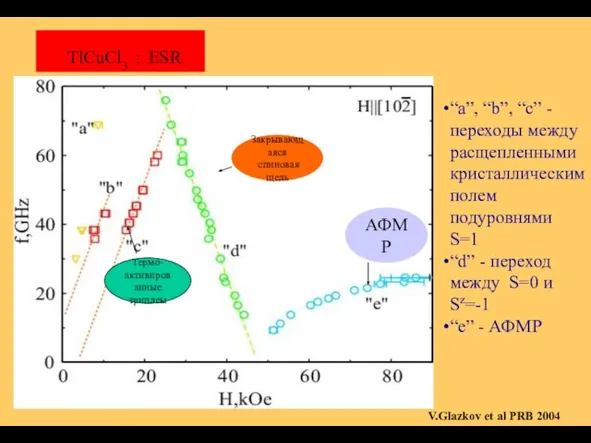
TlCuCl3 : ESR
V.Glazkov et al PRB 2004
Закрывающаяся
спиновая щель
Термо-
активированные
триплеы
АФМР
“a”, “b”, “c” - переходы между расщепленными кристаллическим полем подуровнями S=1
“d” - переход между S=0 и Sz=-1
“e” - АФМР

TCuCl3: магнитный резонанс термоактивированных триплетов
H||[10-2]
V.Glazkov et al PRB 2004

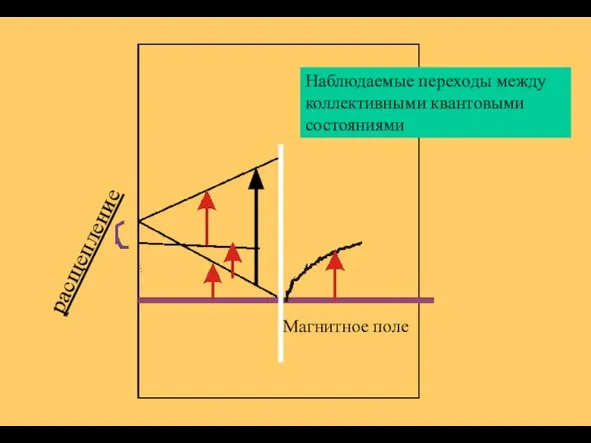
Наблюдаемые переходы между коллективными квантовыми состояниями
расщепление
Магнитное поле

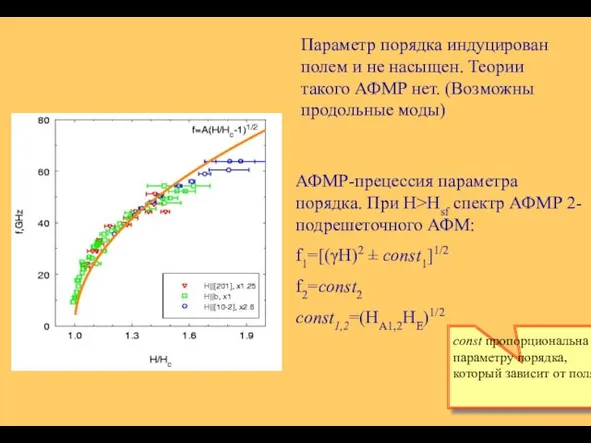
Параметр порядка индуцирован полем и не насыщен. Теории такого АФМР нет. (Возможны продольные моды)
АФМР-прецессия параметра порядка. При H>Hsf спектр АФМР 2-подрешеточного АФМ:
f1=[(γH)2 ± const1]1/2
f2=const2
const1,2=(HA1,2HE)1/2