Комбинации шара (сферы) с многогранниками и фигурами вращения

Шар (сфера) называются описанными около многогранника, если все вершины многогранника принадлежат поверхности шара (сфере).
R
R
R
R
R
R
R
R – радиус шара (сферы), описанных около многогранника.

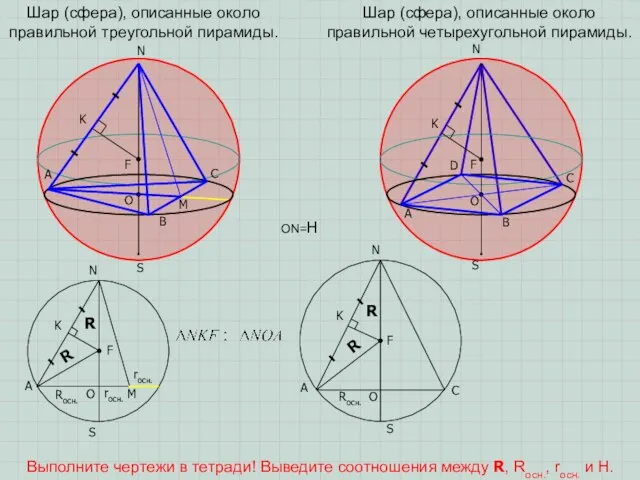
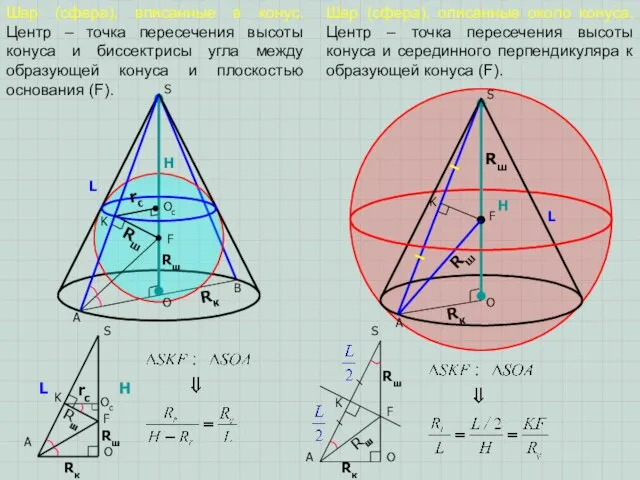
ПРИМЕЧАНИЕ 1. Около любой правильной пирамиды можно описать сферу (шар). Центр этой сферы (шара) – точка пересечения прямой, содержащей высоту пирамиды и серединного перпендикуляра к боковому ребру, проведенному в плоскости, содержащей высоту и боковое ребро пирамиды.
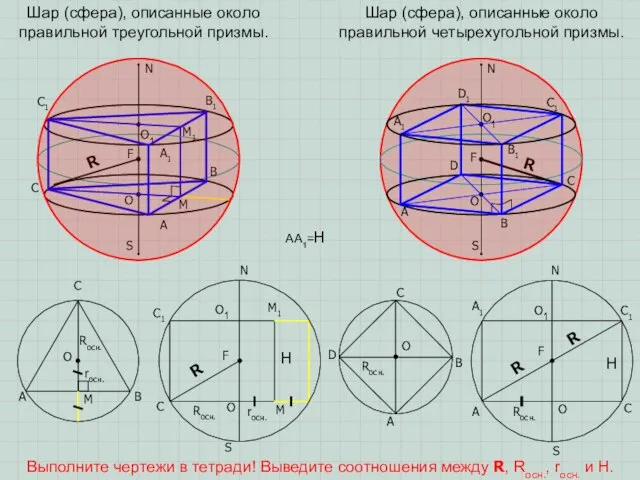
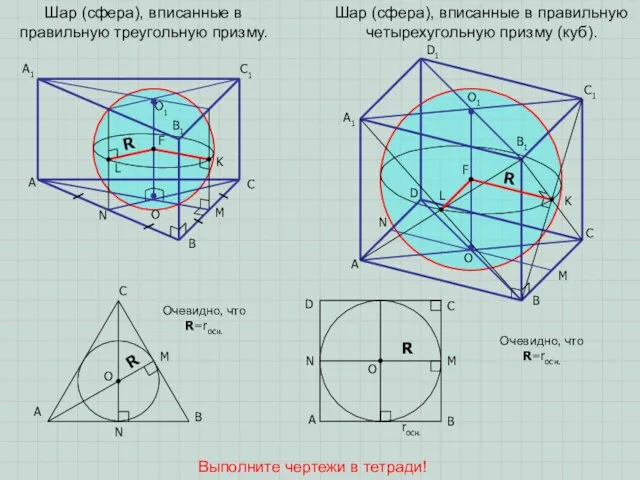
ПРИМЕЧАНИЕ 2. Около любой правильной призмы можно описать сферу (шар). Центр этой сферы (шара) – середина отрезка, соединяющего центры описанных около оснований призмы окружностей.
ПРИМЕЧАНИЕ 3. Если около основания прямой призмы можно описать окружность, то около призмы можно описать сферу (шар). Центром описанной сферы (шара) является середина отрезка, соединяющего центры описанных около основания призмы окружностей.
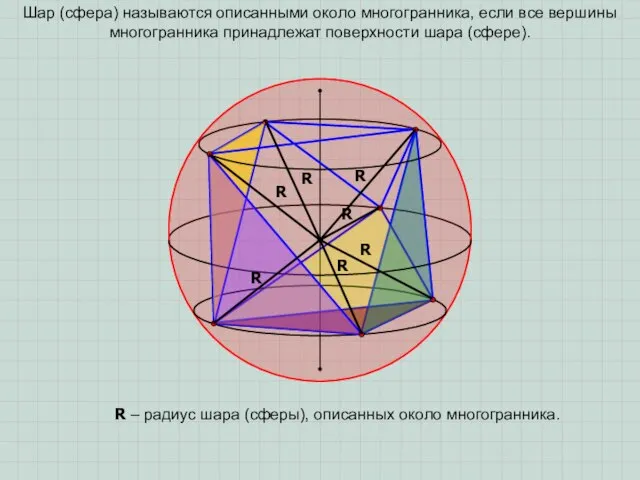
Напомним, что:
около любого треугольника можно описать окружность;
около четырехугольника можно описать окружность, если суммы его противоположных углов равны 1800 (прямоугольник, квадрат, равнобокая трапеция и т.д.);
около любого правильного многоугольника можно описать окружность.

R
R
Шар (сфера), описанные около правильной треугольной призмы.
Шар (сфера), описанные около правильной четырехугольной призмы.
B
C
D
A
B
C
S
N
A
F
O
F
N
S
B1
C1
M1
A1
O1
B1
C1
A1
O1
D1
Выполните чертежи в тетради! Выведите соотношения между R, Rосн., rосн. и H.
O
F
R
A
A1
C
C1
O
O1
D
B
C
A
S
N
B
C
A
O
M
O
F
O1
C
C1
M
M1
R
rосн.
Rосн.
rосн.
Rосн.
Rосн.
Rосн.
R
N
S
H
H
AA1=H
O
M

Шар (сфера), описанные около правильной четырехугольной пирамиды.
Шар (сфера), описанные около правильной треугольной пирамиды.
F
B
C
S
A
D
O
N
C
A
S
A
F
O
M
N
rосн.
Rосн.
R
rосн.
R
R
S
N
F
R
O
Rосн.
Выполните чертежи в тетради! Выведите соотношения между R, Rосн., rосн. и H.
ON=H
B
C
A
F
O
M
S
N
K
K
K
K

Шар (сфера) называются вписанными в многогранник, если все грани многогранника касаются поверхности шара (сферы).
Напомним, что касательная плоскость перпендикулярна радиусу шара (сферы), проведенному к точке касания!

ПРИМЕЧАНИЕ 2. Если в основание пирамиды можно вписать окружность, а основание высоты пирамиды является центром этой окружности, то в пирамиду можно вписать сферу (шар).
ПРИМЕЧАНИЕ 1. В любую правильную пирамиду можно вписать сферу (шар). Центр этой сферы (шара) – точка пересечения высоты пирамиды и биссектрисы двугранного угла между боковой гранью и плоскостью основания пирамиды.
ПРИМЕЧАНИЕ 3. Если в основание прямой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности, то в призму можно вписать сферу (шар). Центром вписанной сферы (шара) является середина отрезка, соединяющего центры вписанных в основания призмы окружностей.
Напомним, что:
в любой треугольник можно вписать окружность;
в четырехугольник можно вписать окружность, если суммы его противоположных сторон равны (квадрат, ромб и т.д.);
в любой правильный многоугольник можно вписать окружность.

B
C
S
M
N
O
L
A
K
F
C
S
N
O
F
L
NFL= NFO⇒
⇒∠LNF=∠ONF
B
C
S
M
N
O
K
A
F
S
M
N
O
K
F
MFK= MFO⇒
⇒∠KMF=∠OMF
Шар (сфера), вписанные в правильную треугольную пирамиду.
Шар (сфера), вписанные в правильную четырехугольную пирамиду.
Достаточно рассмотреть сечение NSC:
Достаточно рассмотреть сечение NSM:
rосн.
Rосн.
D
rосн.
R
R
R
R
OS=H
Выполните чертежи в тетради! Выведите соотношения между R, Rосн., rосн. и H.

B
C
M
N
O
L
A
F
B
C
A
D
B1
C1
A1
D1
Шар (сфера), вписанные в правильную треугольную призму.
Шар (сфера), вписанные в правильную четырехугольную призму (куб).
B1
C1
A1
F
O
O1
O1
K
K
L
Выполните чертежи в тетради!
B
C
A
M
N
O
B
C
A
D
O
M
N
M
N
Очевидно, что R=rосн.
rосн.
Очевидно, что R=rосн.
R
R
R
R

Rш
Rш
Rк
O
F
L
A
S
H
K
Rш
Шар (сфера), вписанные в конус. Центр – точка пересечения высоты конуса и биссектрисы угла между образующей конуса и плоскостью основания (F).
Шар (сфера), описанные около конуса. Центр – точка пересечения высоты конуса и серединного перпендикуляра к образующей конуса (F).
B
O
A
F
S
Oс
K
H
L
Rк
S
O
A
F
K
Rк
Rш
H
L
Rш
rс
rс
Oс
Rш
Rш
Rк
S
O
A
F
K
Rш

Шар (сфера), вписанные в цилиндр. Центр – середина отрезка, соединяющего центры оснований цилиндра.
Шар (сфера), описанные около цилиндра. Центр – середина отрезка, соединяющего центры оснований цилиндра.
F
Rш
F
Rш
O
Rц
O
Rц
H
H
D
C
B
A
Осевое сечение ABCD – квадрат. Цилиндр – равносторонний.