Слайд 2Цель презентации – обеспечить максимальную наглядность изучения темы.
Цели урока:
- Сформировать у учащихся

навыки выполнения арифметических действий с комплексными числами;
Способствовать развитию познавательного интереса учащихся;
Создание условий для формирования интеллектуальной и творческой видов компетентностей.
Слайд 3План урока:
актуализация опорных знаний;
(фронтальный опрос)
геометрическая интерпретация комплексных чисел;
краткая историческая справка;
геометрическое изображение суммы

и разности комплексных чисел;
закрепление изученного материала на практике;
итоги урока.
Слайд 4Актуализация опорных знаний.
Чем вызвана необходимость расширения множества действительных чисел?
Дать определение комплексного числа.
Сформулировать

условие равенства двух комплексных чисел
Дать определение сопряженных комплексных чисел. Привести примеры.
Слайд 5Актуализация опорных знаний.
Выполнить действия:
1) (7+3i)+(4-2i)-(1-4i)=
10+5i
2)8i*4i=
-32

Слайд 6Актуализация опорных знаний.
3) (2-i)*(-5)=
-10+5i
4)

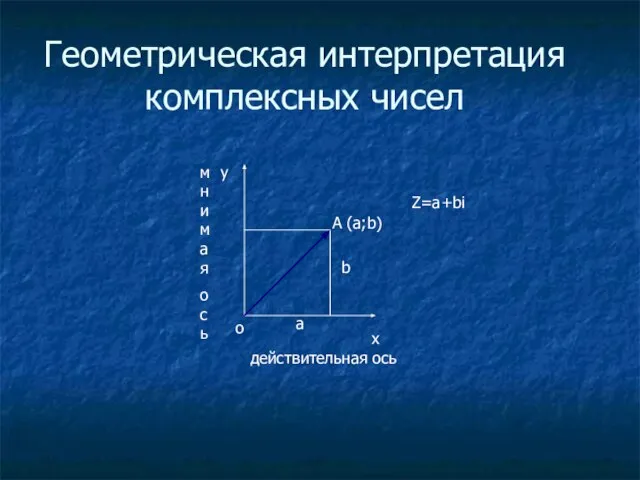
Слайд 7Геометрическая интерпретация комплексных чисел
х
у
о
А (a;b)
а
b
Z=а+bi
действительная ось
мнимая
ось
Слайд 8Историческая справка
Понятие «модуль» и «аргумент» комплексного числа ввел французский ученый Жан Лерон

Д Аламбер
Геометрическое истолкование комплексных чисел и действий над ними окончательно закрепилось в математике после выхода работы немецкого математика Фридриха Гаусса «Теория биквадратных излишков. Гаусс Заменил название «мнимые числа» на термин «комплексные»
Слайд 9Историческая справка
Историческая справка

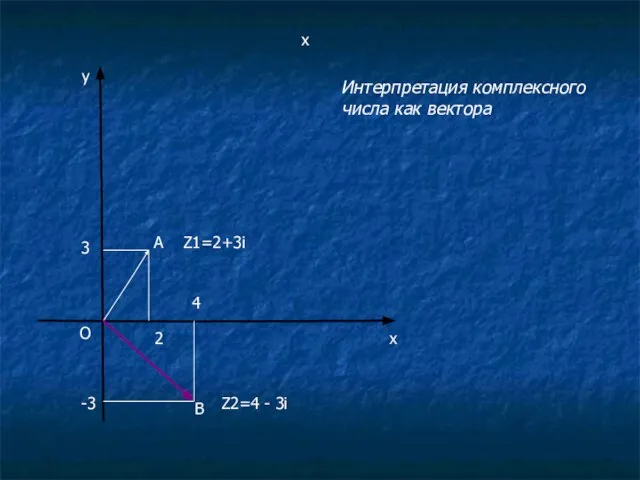
Слайд 10х
х
у
О
А
2
3
Z1=2+3i
B
4
-3
Z2=4 - 3i
Интерпретация комплексного числа как вектора
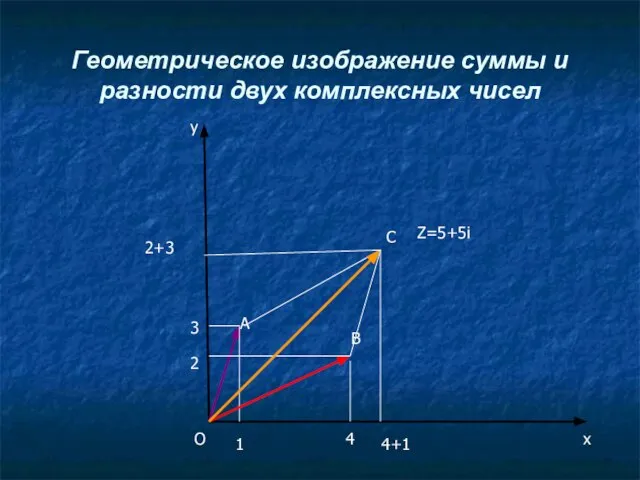
Слайд 11Геометрическое изображение суммы и разности двух комплексных чисел
у
х
А
О
1
3
4
2
В
С
4+1
2+3
Z=5+5i
Слайд 12Геометрическое изображение суммы и разности двух комплексных чисел
Найти геометрическое изображение разности комплексных
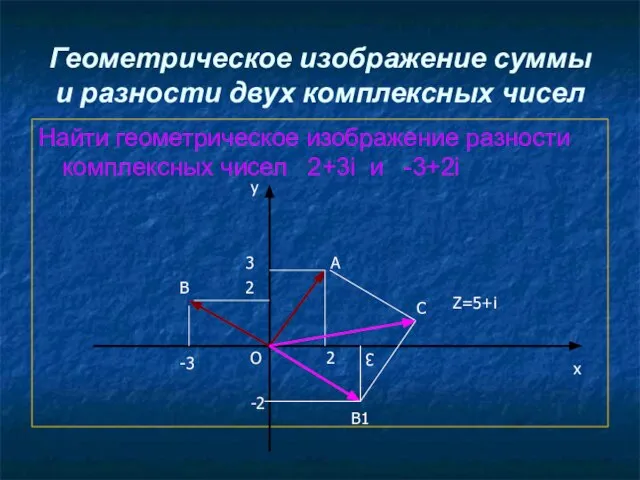
чисел 2+3i и -3+2i
у
х
О
А
2
3
В
-3
2
В1
3
-2
С
Z=5+i
Слайд 13Восприятие и осознание нового материала
Выполните сложение и вычитание комплексных чисел в геометрической
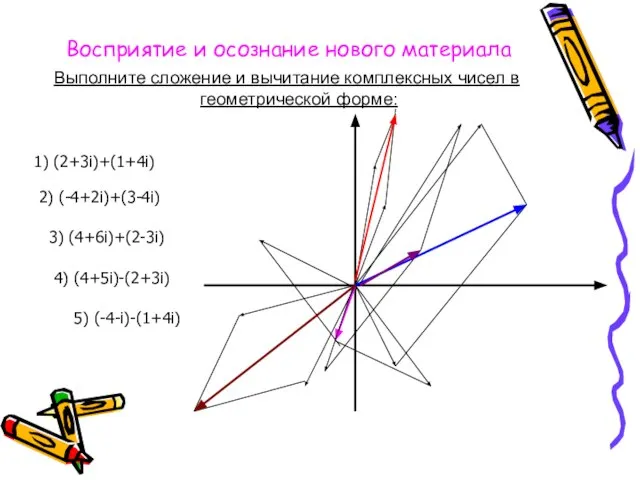
форме:
1) (2+3i)+(1+4i)
2) (-4+2i)+(3-4i)
3) (4+6i)+(2-3i)
4) (4+5i)-(2+3i)
5) (-4-i)-(1+4i)












 Спасо-Преображенский собор (г. Переславль-Залесский. Храмы Золотого кольца России)
Спасо-Преображенский собор (г. Переславль-Залесский. Храмы Золотого кольца России) Презентация на тему Скорость. Время. Расстояние 3 класс
Презентация на тему Скорость. Время. Расстояние 3 класс Род несклоняемых существительных (5 класс)
Род несклоняемых существительных (5 класс) Промышленные подходы привлечения поискового трафика
Промышленные подходы привлечения поискового трафика Планируемое количество мест по направлениям подготовки/специальностям на 2017/2018 учебный год
Планируемое количество мест по направлениям подготовки/специальностям на 2017/2018 учебный год Imperfectum indicativi activi et passivi (прошедшее время несовершенного вида изъявительного наклонения )
Imperfectum indicativi activi et passivi (прошедшее время несовершенного вида изъявительного наклонения ) Пример портфолио
Пример портфолио Учебные мотивы на разных этапах онтогенеза.
Учебные мотивы на разных этапах онтогенеза. 5 октября празднуется Всемирный ДЕНЬ УЧИТЕЛЯ! И мы, ученики 3 «Б» класса лицея № 6 г. Бердска, подготовили поздравления для наш
5 октября празднуется Всемирный ДЕНЬ УЧИТЕЛЯ! И мы, ученики 3 «Б» класса лицея № 6 г. Бердска, подготовили поздравления для наш Информационная бизнес-платформа InterKent
Информационная бизнес-платформа InterKent Книги, которые нужно прочитать до 25 лет
Книги, которые нужно прочитать до 25 лет «ЧТОБЫ ЗНАЛИ И ПОМНИЛИ !»
«ЧТОБЫ ЗНАЛИ И ПОМНИЛИ !» ехали, ехали
ехали, ехали Famous people o Great Britain
Famous people o Great Britain Этапы разработки и исследования моделей на компьютере
Этапы разработки и исследования моделей на компьютере 20161210_9_klass_ugolnaya_prom
20161210_9_klass_ugolnaya_prom Каранин
Каранин Михаил Александрович Шолохов
Михаил Александрович Шолохов Деловой этикет. Лекция 8
Деловой этикет. Лекция 8 Элементы фирменного стиля предприятия
Элементы фирменного стиля предприятия Электрические машины
Электрические машины Правила безопасного поведения во время зимних каникул
Правила безопасного поведения во время зимних каникул Валы и оси
Валы и оси Квиллинг
Квиллинг Элетронная таблица Excel
Элетронная таблица Excel Рождество в неоновом свете
Рождество в неоновом свете Презентация V.I.C.
Презентация V.I.C. Основные глобальные проблемы пленеты Земля
Основные глобальные проблемы пленеты Земля