Содержание
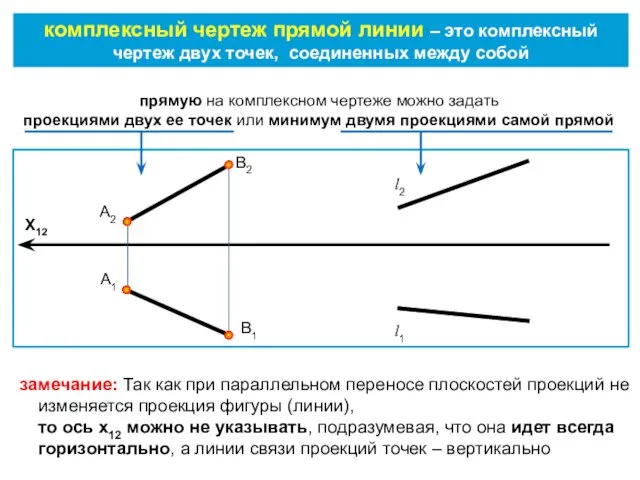
- 2. комплексный чертеж прямой линии – это комплексный чертеж двух точек, соединенных между собой X12 А2 А1
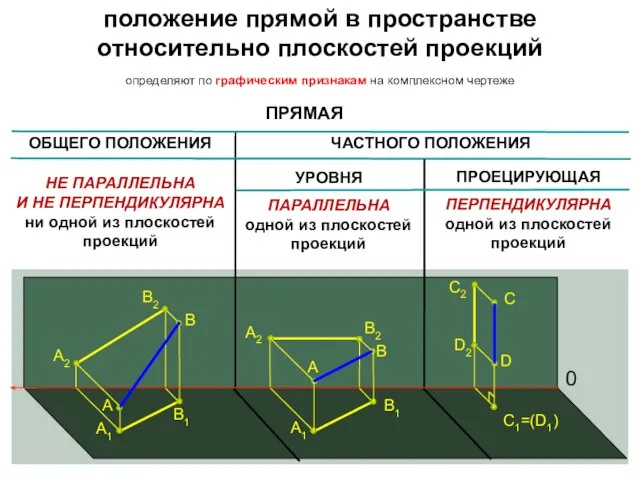
- 3. положение прямой в пространстве относительно плоскостей проекций A1 B1 A A2 B B2 A1 B1 A
- 4. ПРЯМЫЕ ОБЩЕГО ПОЛОЖЕНИЯ
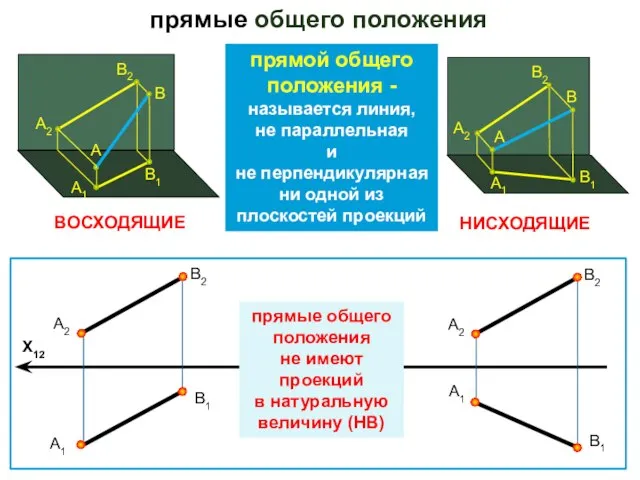
- 5. прямые общего положения X12 А2 А1 В1 В2 ВОСХОДЯЩИЕ НИСХОДЯЩИЕ А2 А1 В1 В2 прямой общего
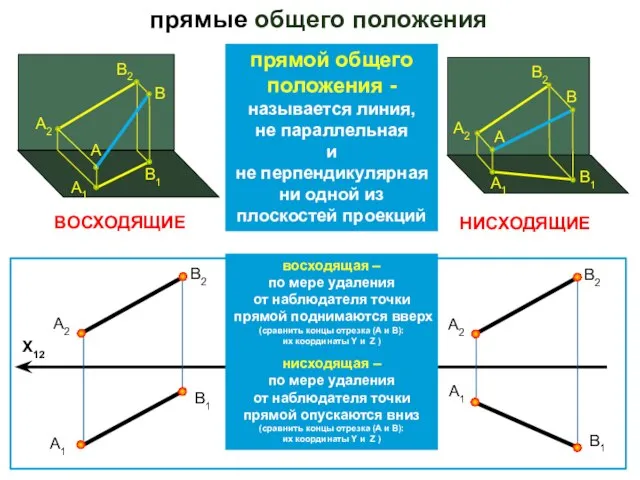
- 6. прямые общего положения X12 А2 А1 В1 В2 ВОСХОДЯЩИЕ НИСХОДЯЩИЕ А2 А1 В1 В2 прямой общего
- 7. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ: ПРЯМЫЕ УРОВНЯ, ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ
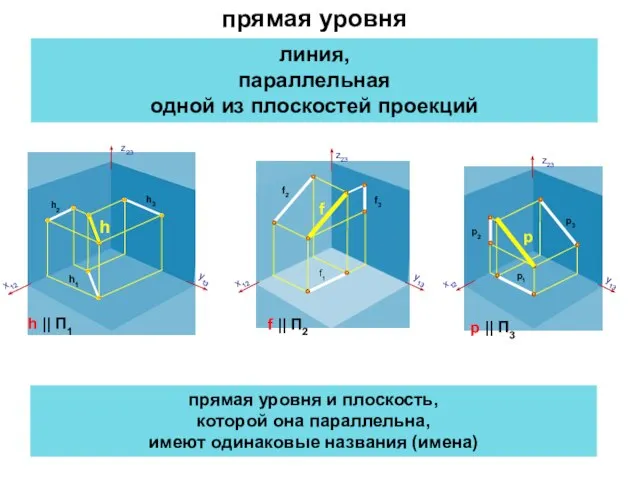
- 8. прямая уровня и плоскость, которой она параллельна, имеют одинаковые названия (имена) прямая уровня линия, параллельная одной
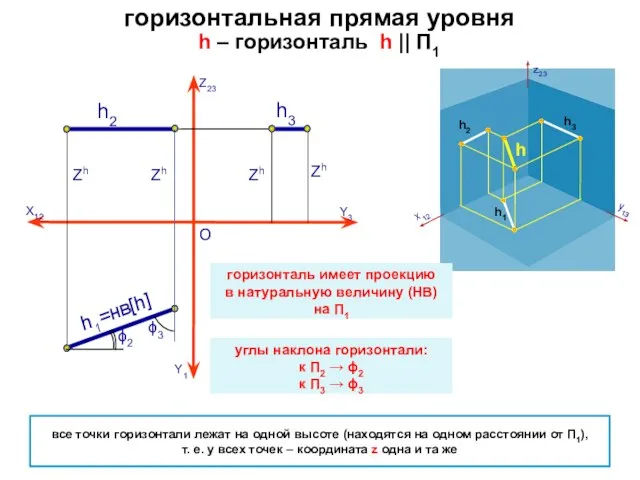
- 9. h – горизонталь h || П1 горизонтальная прямая уровня О все точки горизонтали лежат на одной
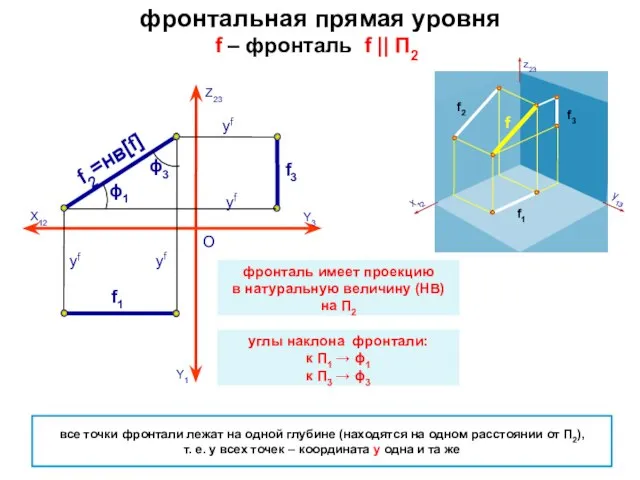
- 10. фронтальная прямая уровня f – фронталь f || П2 О все точки фронтали лежат на одной
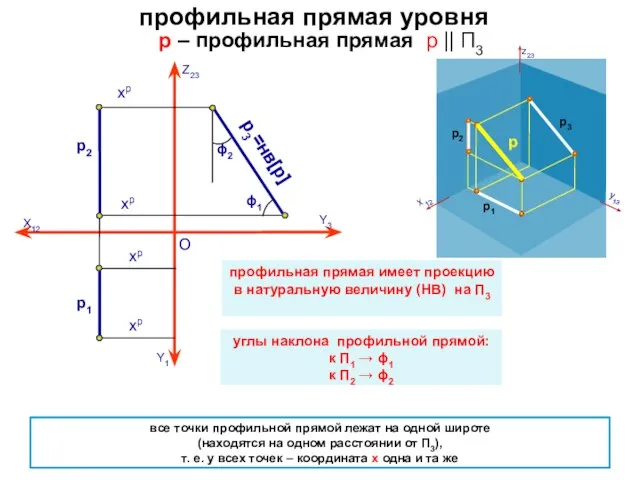
- 11. профильная прямая уровня р – профильная прямая p || П3 О все точки профильной прямой лежат
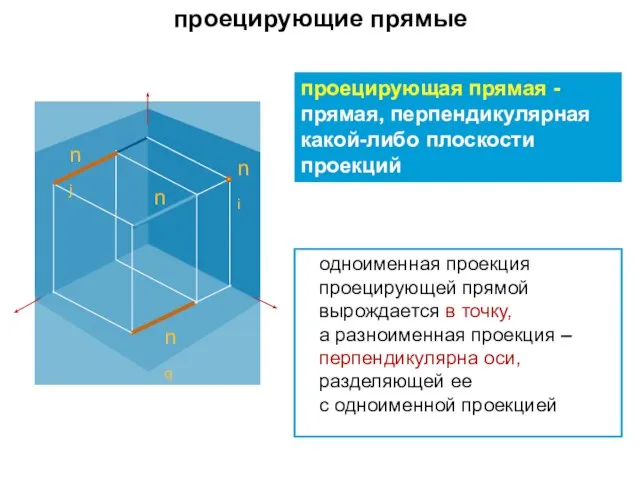
- 12. проецирующая прямая - прямая, перпендикулярная какой-либо плоскости проекций одноименная проекция проецирующей прямой вырождается в точку, а
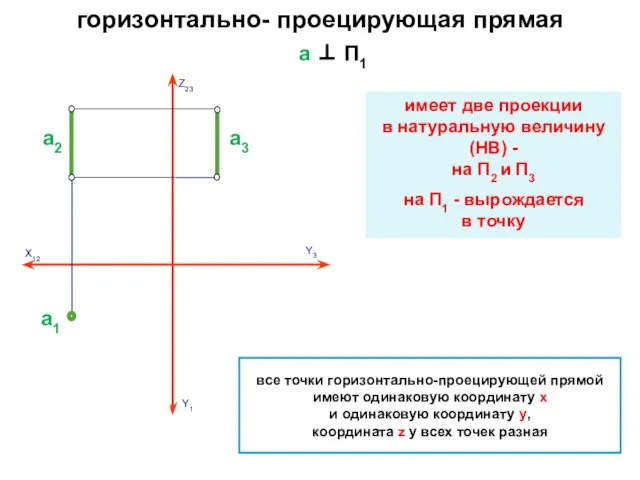
- 13. горизонтально- проецирующая прямая a ⊥ П1 имеет две проекции в натуральную величину (НВ) - на П2
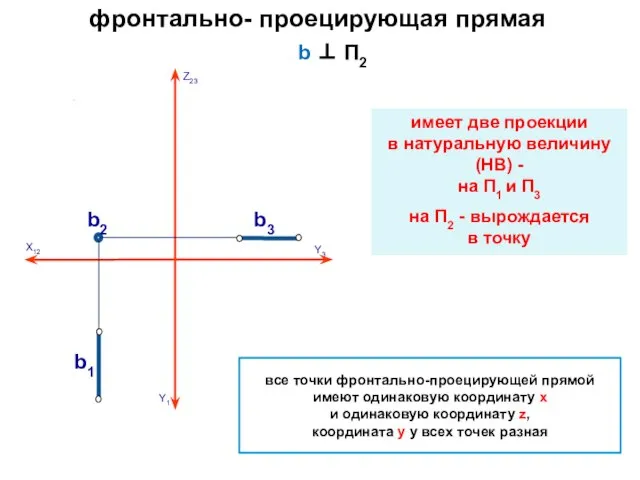
- 14. фронтально- проецирующая прямая b ⊥ П2 имеет две проекции в натуральную величину (НВ) - на П1
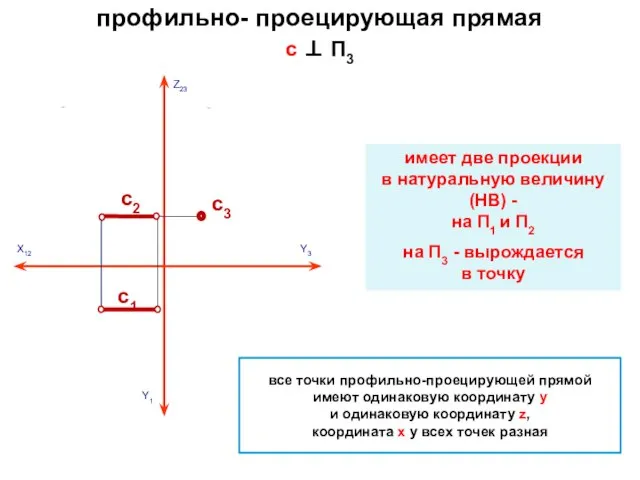
- 15. профильно- проецирующая прямая c ⊥ П3 имеет две проекции в натуральную величину (НВ) - на П1
- 16. прямые уровня: - наличие одной проекции в натуральную величину, - две другие проекции параллельны координатным осям,
- 17. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ
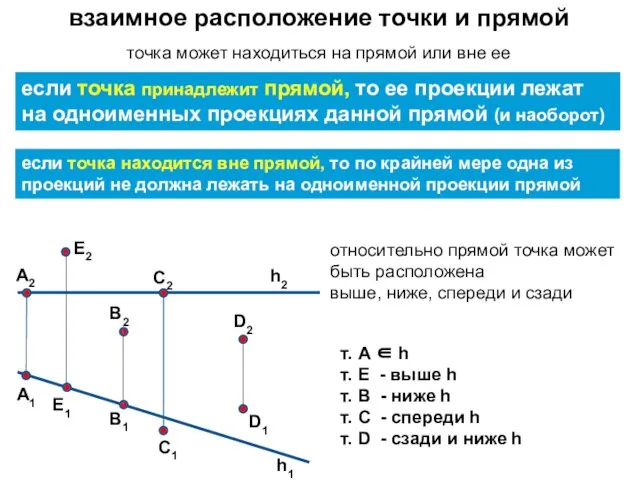
- 18. взаимное расположение точки и прямой точка может находиться на прямой или вне ее если точка принадлежит
- 19. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
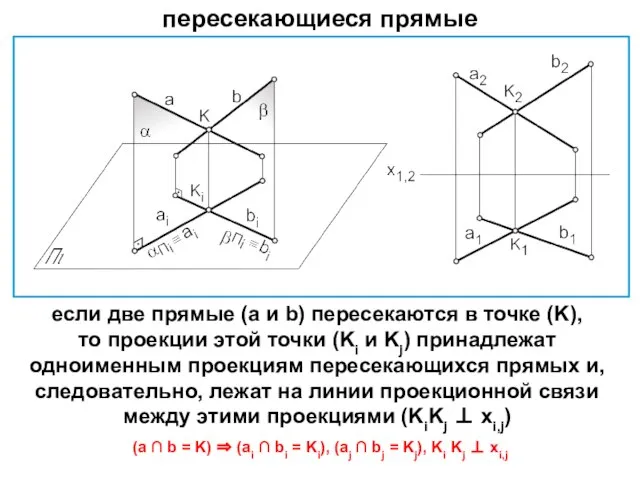
- 20. пересекающиеся прямые если две прямые (a и b) пересекаются в точке (K), то проекции этой точки
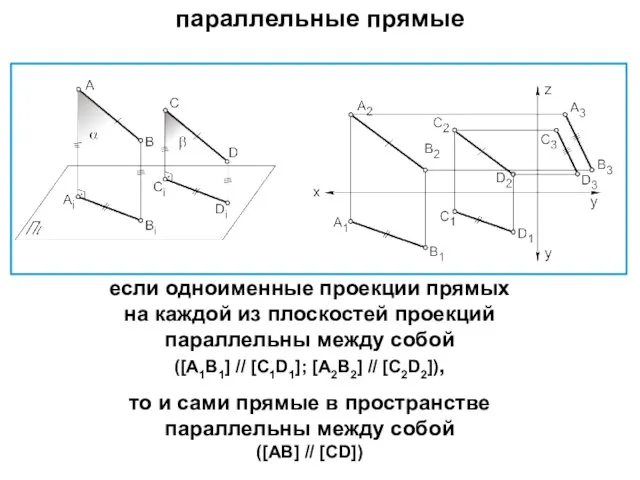
- 21. если одноименные проекции прямых на каждой из плоскостей проекций параллельны между собой ([A1B1] // [C1D1]; [A2B2]
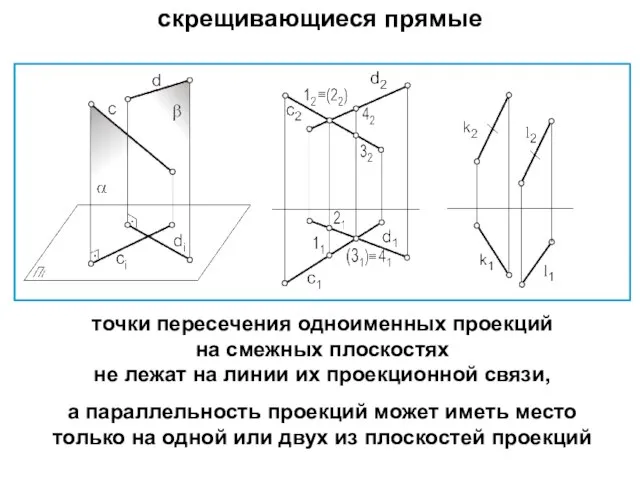
- 22. скрещивающиеся прямые точки пересечения одноименных проекций на смежных плоскостях не лежат на линии их проекционной связи,
- 23. ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ ЛИНИИ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ЭТОЙ ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ
- 24. натуральная величина отрезка прямой способ прямоугольного треугольника Дано: [АВ] ; [АiBi]; [AjBj] теорема: Натуральная величина отрезка
- 25. Пi Пj Xi,j Aj Ai Вj B Bi A BI BIj kB kA kAB kAB ///
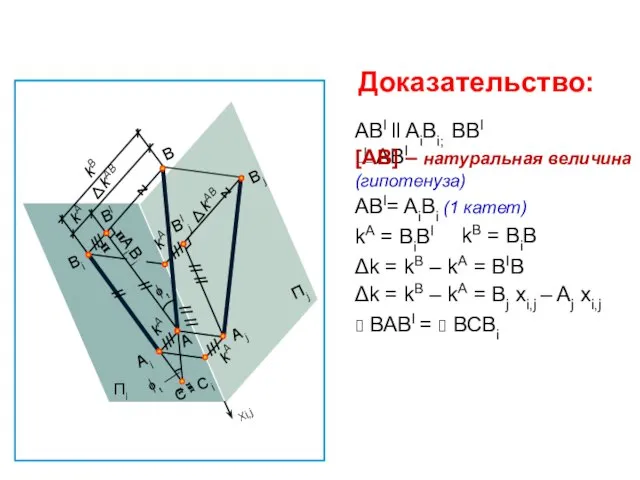
- 26. [АВ] – натуральная величина (гипотенуза ) α - угол наклона отрезка АВ к плоскости П1 и
- 27. [АВ] – натуральная величина (гипотенуза ) α - угол наклона отрезка АВ к плоскости П1 и
- 28. НАХОЖДЕНИЕ НЕДОСТАЮЩЕЙ ПРОЕКЦИИ ТОЧКИ НА ПРОФИЛЬНОЙ ПРЯМОЙ
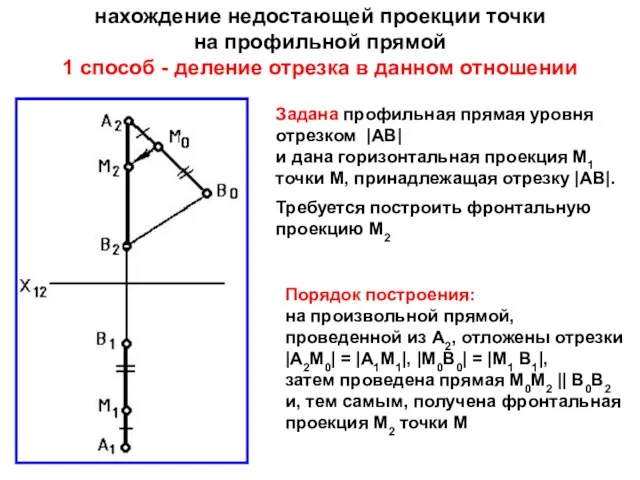
- 29. нахождение недостающей проекции точки на профильной прямой 1 способ - деление отрезка в данном отношении Задана
- 31. Скачать презентацию






![натуральная величина отрезка прямой способ прямоугольного треугольника Дано: [АВ] ; [АiBi]; [AjBj]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/887988/slide-23.jpg)
![[АВ] – натуральная величина (гипотенуза ) α - угол наклона отрезка АВ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/887988/slide-25.jpg)
![[АВ] – натуральная величина (гипотенуза ) α - угол наклона отрезка АВ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/887988/slide-26.jpg)

 В мире боевых искусств
В мире боевых искусств Политические партии
Политические партии Zrozumieć kobietę
Zrozumieć kobietę Северный Ледовитый океан 7 класс
Северный Ледовитый океан 7 класс Образование в области прав ребенка как мультикультурный проект
Образование в области прав ребенка как мультикультурный проект Государство как субъект МЧП. Лекция 7
Государство как субъект МЧП. Лекция 7 Сложные проценты на фондовом рынке
Сложные проценты на фондовом рынке Измерительная техника
Измерительная техника Колобок в стране
Колобок в стране Современные масс-медиа о событиях Второй Мировой войны: структурный анализ дискурса вражды
Современные масс-медиа о событиях Второй Мировой войны: структурный анализ дискурса вражды Презентация на тему Симметрия в природе
Презентация на тему Симметрия в природе Would you like to join our sport club?
Would you like to join our sport club? Департамент специальных событий
Департамент специальных событий Структура питч-презентации
Структура питч-презентации Волшебные нотки
Волшебные нотки Клубы по интересам
Клубы по интересам  Л.В. Чайка, методист ГРЦИО «Тьютор»
Л.В. Чайка, методист ГРЦИО «Тьютор» Господин Митюков и его стипендии
Господин Митюков и его стипендии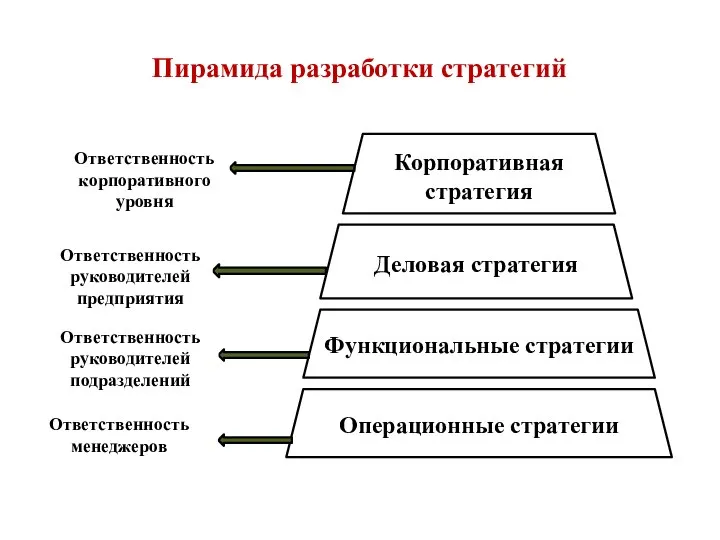 Пирамида разработки стратегий
Пирамида разработки стратегий Презентация
Презентация Презентация по английскому Использование smart board на уроках английского языка
Презентация по английскому Использование smart board на уроках английского языка  Магнитное поле тока
Магнитное поле тока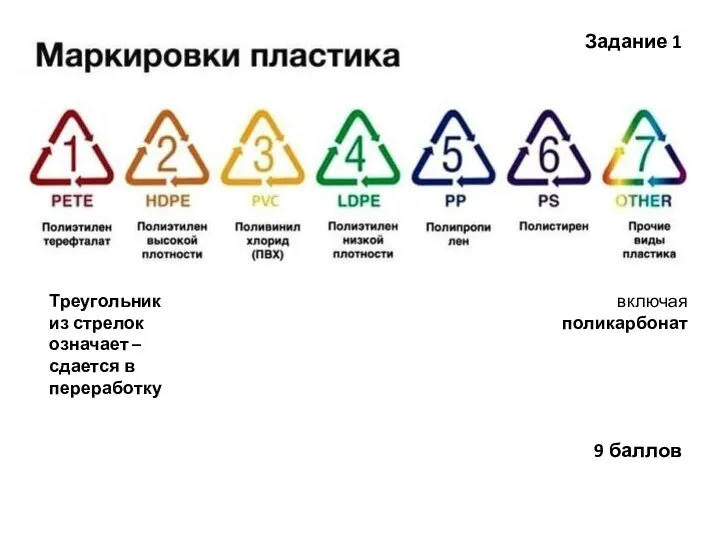 Маркировка пластика
Маркировка пластика Самопрезентация. Пермякова Анастасия Даниловна
Самопрезентация. Пермякова Анастасия Даниловна Фитоиндикация типов леса по А. С. Барабанщикову по Д. А. Цыганову в сравнении с Погребняком
Фитоиндикация типов леса по А. С. Барабанщикову по Д. А. Цыганову в сравнении с Погребняком Иконы Богородицы в истории России
Иконы Богородицы в истории России Федеральный государственный образовательный стандарт общего образования: актуальные вопросы введенияИюль 2010 г.
Федеральный государственный образовательный стандарт общего образования: актуальные вопросы введенияИюль 2010 г. Что такое КПК. Зачем нужен кредитный потребительский кооператив
Что такое КПК. Зачем нужен кредитный потребительский кооператив