Конус

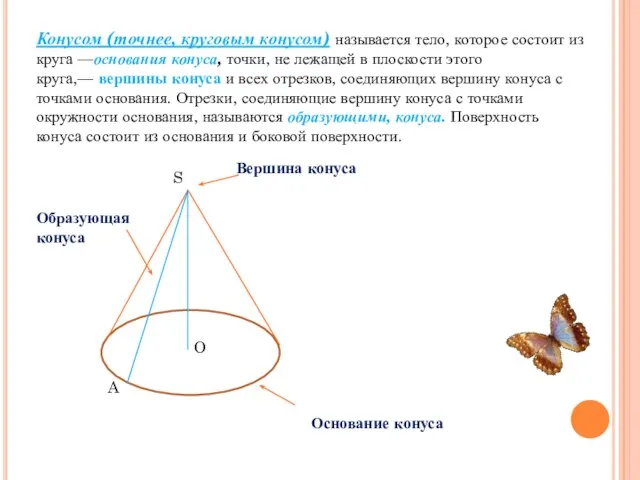
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга —основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.
Вершина конуса
Основание конуса

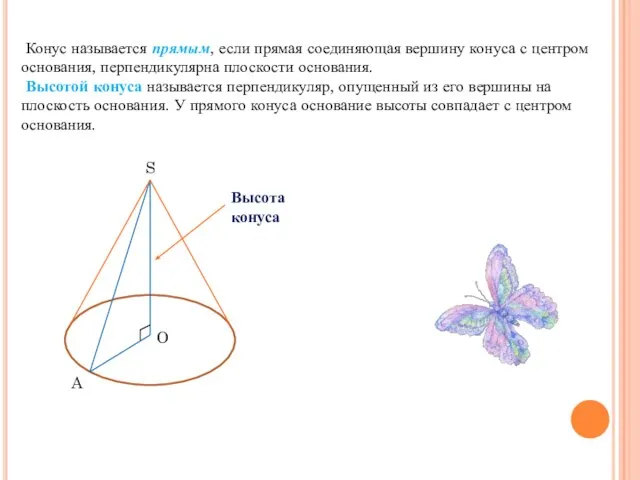
Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.
Высота конуса

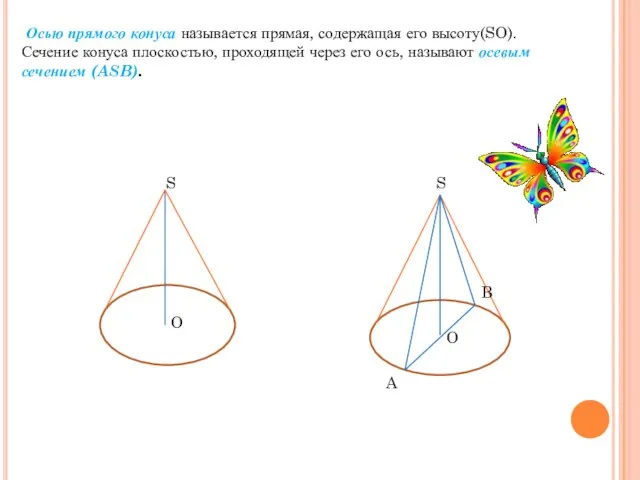
Осью прямого конуса называется прямая, содержащая его высоту(SO).
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением (ASB).

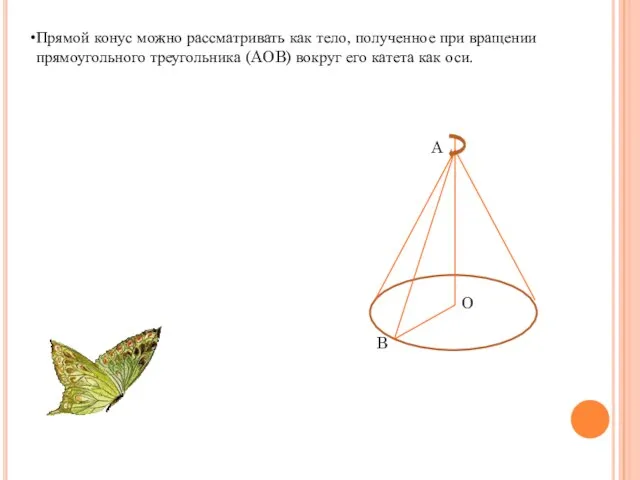
Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника (AOB) вокруг его катета как оси.

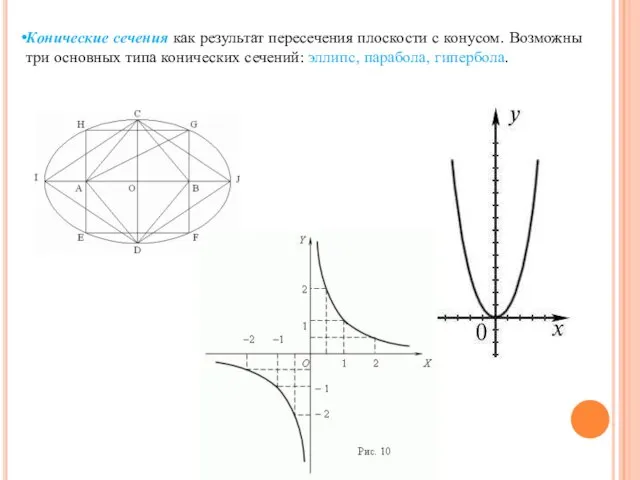
Конические сечения как результат пересечения плоскости с конусом. Возможны три основных типа конических сечений: эллипс, парабола, гипербола.

Сечение конуса плоскостью
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса .

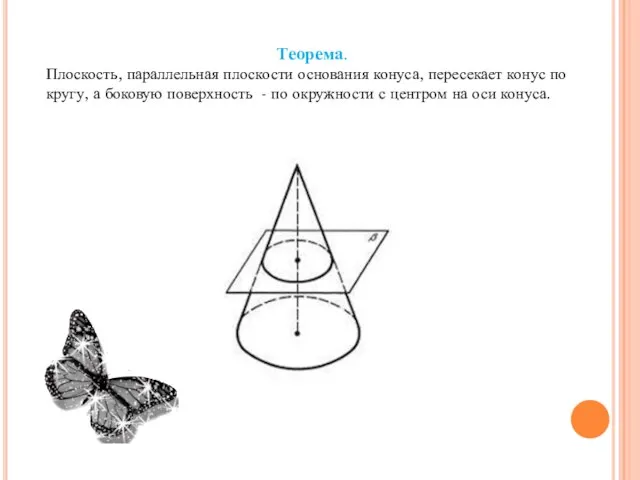
Теорема.
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса.

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую .

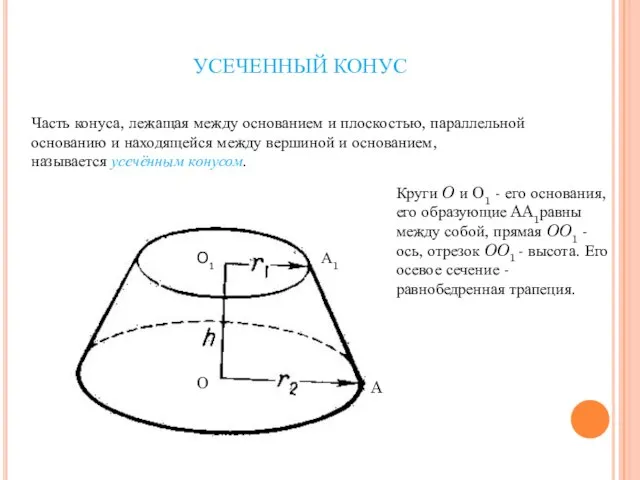
УСЕЧЕННЫЙ КОНУС
Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом.
Круги O и O1 - его основания, его образующие AA1равны между собой, прямая OO1 - ось, отрезок OO1 - высота. Его осевое сечение - равнобедренная трапеция.
O
A
О1
А1

Площадь боковой поверхности конуса: Sбок=ПRL
Площадь полной поверхности конуса: Sпол= ПRL+ПR2
Объем конуса: V=1/3ПR2H
ФОРМУЛЫ

ФОРМУЛЫ
Площадь боковой поверхности усеченного конуса: Sбок=П(R+r)*L
Площадь полной поверхности усеченного конуса: Sпол=ПR2 + Пr2 + П(R+r)L
Объем усеченного конуса: V =1/3ПH(R2 + Rr + r2)

ЗАДАЧКИ

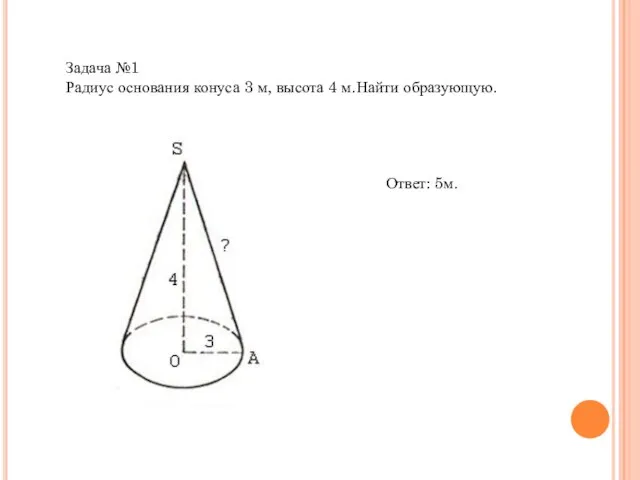
Задача №1
Радиус основания конуса 3 м, высота 4 м.Найти образующую.
Ответ: 5м.

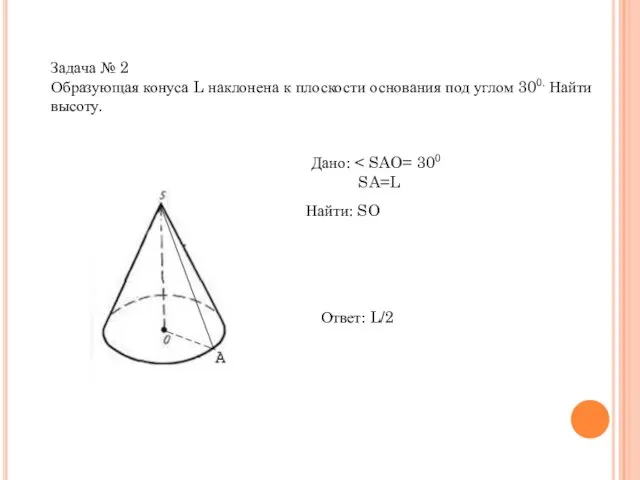
Задача № 2
Образующая конуса L наклонена к плоскости основания под углом 300. Найти высоту.
Дано: < SAO= 300
SA=L
Найти: SO
Ответ: L/2

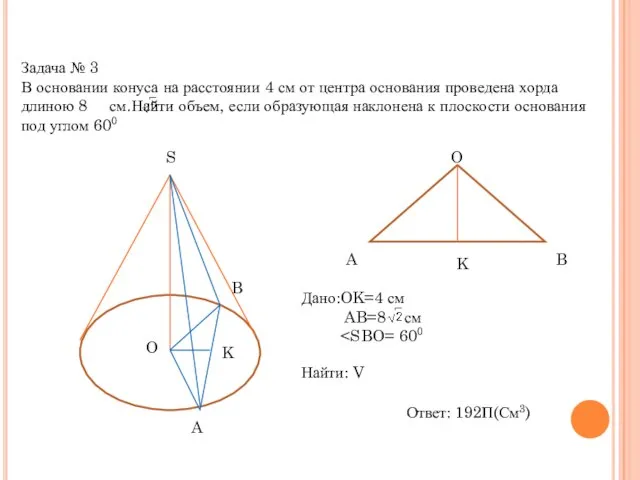
Задача № 3
В основании конуса на расстоянии 4 см от центра основания проведена хорда длиною 8 см.Найти объем, если образующая наклонена к плоскости основания под углом 600
Дано:OK=4 см
AB=8 см
Найти: V
Ответ: 192П(См3)

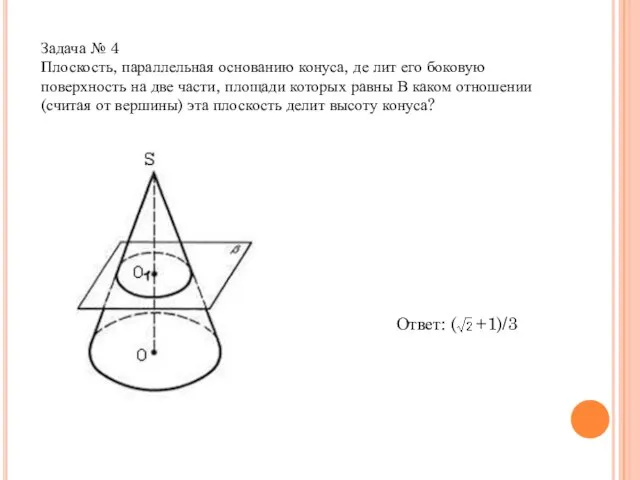
Задача № 4
Плоскость, параллельная основанию конуса, де лит его боковую поверхность на две части, площади которых равны В каком отношении (считая от вершины) эта плоскость делит высоту конуса?
Ответ: ( +1)/3

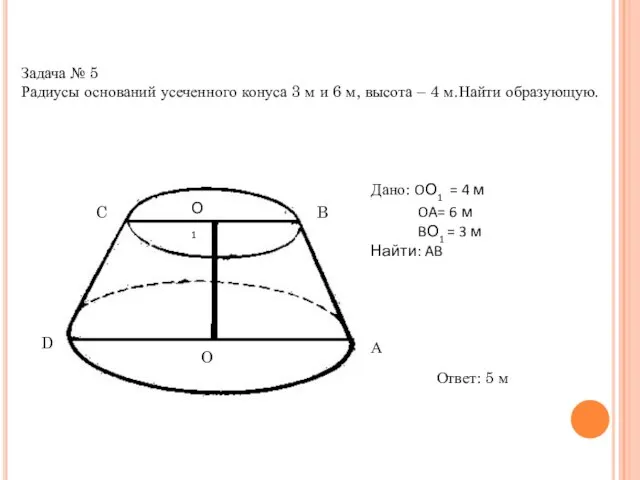
Задача № 5
Радиусы оснований усеченного конуса 3 м и 6 м, высота – 4 м.Найти образующую.
А
B
C
D
O
О1
Дано: OО1 = 4 м
OA= 6 м
BО1 = 3 м
Найти: AB
Ответ: 5 м

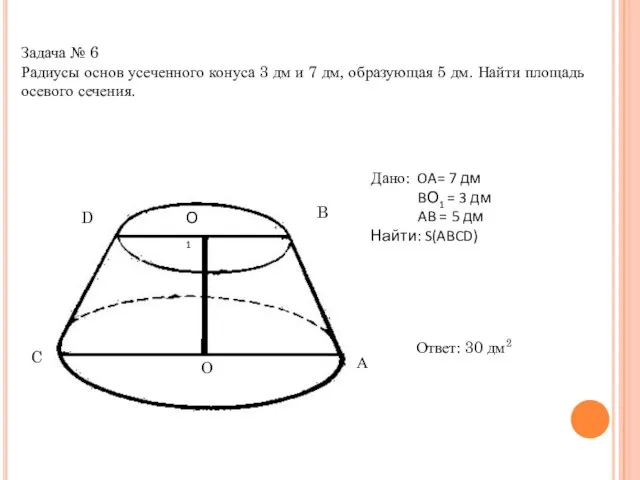
Задача № 6
Радиусы основ усеченного конуса 3 дм и 7 дм, образующая 5 дм. Найти площадь осевого сечения.
C
О1
B
D
O
А
Дано: OA= 7 дм
BО1 = 3 дм
AB = 5 дм
Найти: S(ABCD)
Ответ: 30 дм2

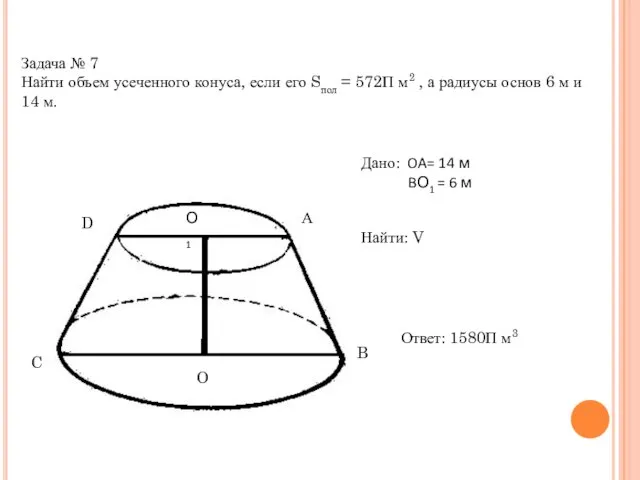
Задача № 7
Найти объем усеченного конуса, если его Sпол = 572П м2 , а радиусы основ 6 м и 14 м.
А
B
C
D
O
О1
Дано: OA= 14 м
BО1 = 6 м
Найти: V
Ответ: 1580П м3