Содержание
- 2. «Уравнение - это золотой ключ, открывающий все математические сезамы». С. Коваль.
- 3. Специальные методы: 1.Метод выделения квадратного двучлена. 2. Метод «переброски» старшего коэффициента. 3. На основании теорем.
- 4. Общие методы: Разложение на множители; Введение новой переменной; Графический метод.
- 5. . Впервые ввёл термин «квадратное уравнение» немецкий философ - знаменитый немецкий философ, родился в 1679 г.
- 6. – английский математик, который ввёл термин «дискриминант». Сильвестр Джеймс Джозеф
- 7. В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов
- 8. Энциклопедия квадратного уравнения
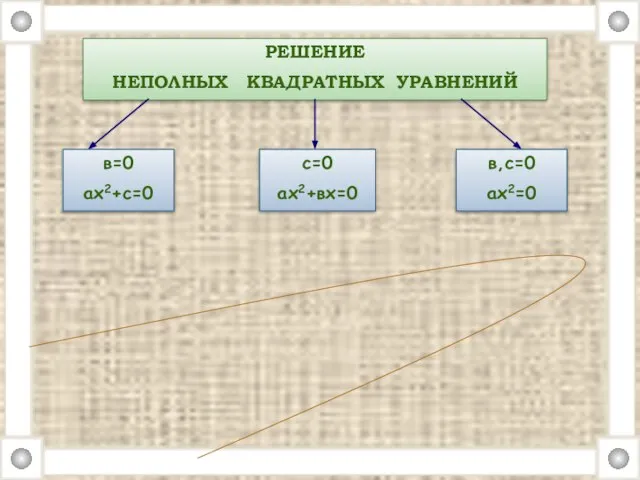
- 9. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ в=0 ах2+с=0 с=0 ах2+вх=0 в,с=0 ах2=0
- 10. Алгоритм решения 1.Переносим с в правую часть уравнения. ах2 = -с. 2.Делим обе части уравнения на
- 11. Выносим x за скобки: х (ах + в) = 0. 2. «Разбиваем» уравнение на два: x
- 12. 1. Делим обе части уравнения на а≠0. х2 = 0 2. Одно решение: х = 0.
- 13. Неполные квадратные уравнения:
- 14. D D = 0 D > 0 Корней нет
- 15. b = 2k (чётное число)
- 16. Теорема Виета x1 и х2 – корни уравнения x1 и х2 – корни уравнения
- 17. Суть метода: привести квадратное уравнение общего вида к неполному квадратному уравнению. Пример: х2 - 6х +
- 18. Корни квадратных уравнений и связаны соотношениями и Пример: Метод «переброски» старшего коэффициента. 2х2 - 9х –
- 19. На основании теорем: Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй
- 20. Метод разложения на множители привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х)
- 21. Введение новой переменной. Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой
- 22. Графический метод Для решения уравнения f(x) = g(x) необходимо построить графики функций y = f(x), y
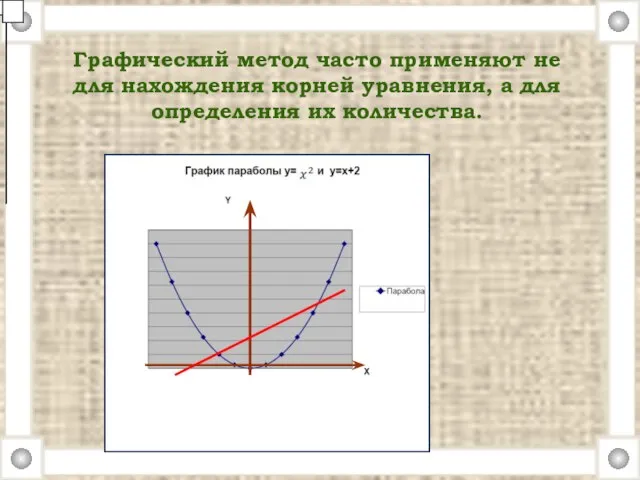
- 23. Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.
- 24. Метод выделения квадрата двучлена. (a + b)2 = a2 + 2ab + b2, (a - b)2
- 25. Метод “переброски” старшего коэффициента ax2 + bx + c = 0 и y2+ by + ac
- 26. Теорема 1. Если в квадратном уравнении a + b + c = 0, то один из
- 27. Теорема 2. Если в квадратном уравнении a + c = b, то один из корней равен
- 28. Метод разложения на множители. Решите уравнение 4х2 + 5х + 1 = 0. 4х2 + 5х
- 30. Скачать презентацию











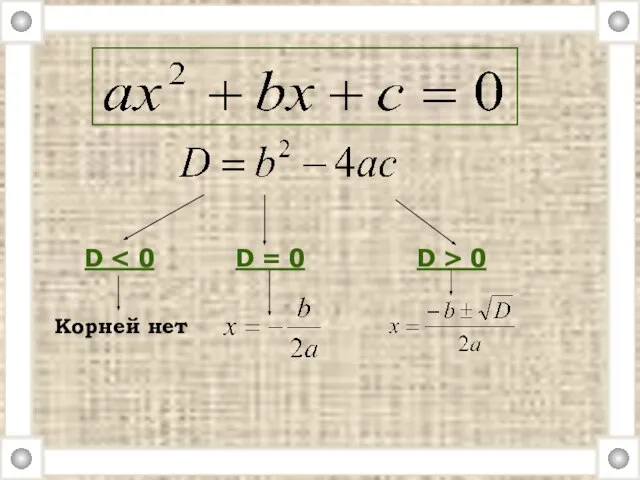













 Презентация на тему Восточная Сибирь
Презентация на тему Восточная Сибирь  Упрощение выражений
Упрощение выражений Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше
Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше Генеалогия
Генеалогия Колизей в Риме
Колизей в Риме 1С-Битрикс: Корпоративный портал
1С-Битрикс: Корпоративный портал Слова антонимы (Противоположности)
Слова антонимы (Противоположности) Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО
Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО Китайский новый год
Китайский новый год 20 причин любить Рёму
20 причин любить Рёму Путь. Перемещение. Определение координаты движущегося тела
Путь. Перемещение. Определение координаты движущегося тела Pancakes day
Pancakes day Критерии и методика отнесения документов к категории для служебного пользования
Критерии и методика отнесения документов к категории для служебного пользования Учебные видеоролики, как ресурс саморазвития
Учебные видеоролики, как ресурс саморазвития Система Box-Design & Nevo
Система Box-Design & Nevo Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова
Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова Дома гороскопа
Дома гороскопа Сложение и вычитание десятичных дробей.
Сложение и вычитание десятичных дробей. Судьба старославянизмов в русском языке
Судьба старославянизмов в русском языке Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула»
Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула» Обобщающий урок по теме:
Обобщающий урок по теме: Маркетинговые исследования
Маркетинговые исследования  Факторы развития когнитивных способностей в процессе обучения
Факторы развития когнитивных способностей в процессе обучения Доступ к данным на основе ado
Доступ к данным на основе ado Весна. Детские рисунки
Весна. Детские рисунки Декларация на товары
Декларация на товары Химическое действие света. Фотография
Химическое действие света. Фотография Моделирование, как метод познания (10 класс)
Моделирование, как метод познания (10 класс)