Содержание
- 2. Окружность Определение: Окружностью называют множество точек плоскости, равноудаленных от данной точки Данная точка называется центром окружности
- 3. Например, составьте уравнение окружности, проходящей через точки А(-2; 5) и В(6; -1), если отрезок АВ является
- 4. у х М(-2; 3) 3 -2
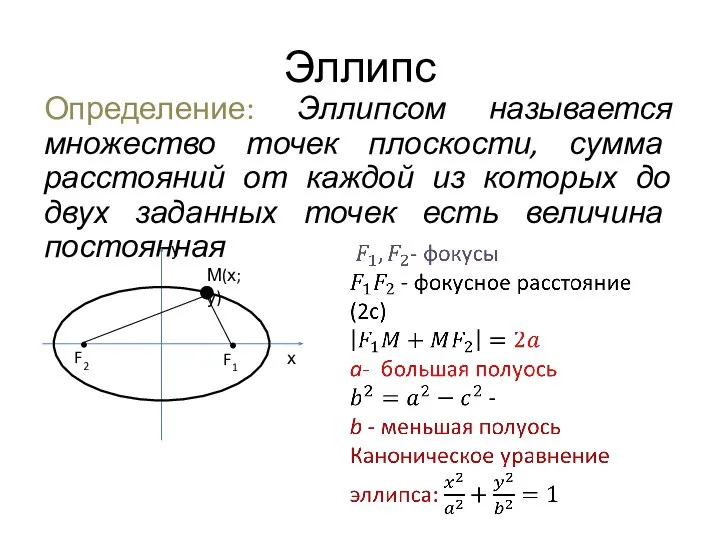
- 5. Эллипс Определение: Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных
- 6. Исследование формы эллипса по его уравнению Значит, эллипс расположен внутри прямоугольника, со сторонами x=a, x=-a, y=b,
- 9. y x 5 -5 3 -3
- 10. -a a b -b x y
- 11. у х a -a b -b
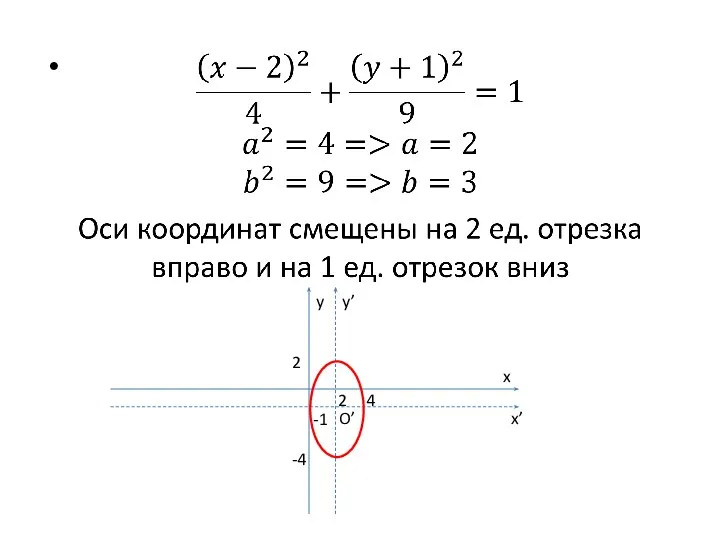
- 12. x y x’ -1 y’ O’ 2 4 2 -4
- 13. Расположение эллипса относительно координатных осей F1(-c;0) F2(c;0) -a a x y -b b y x a
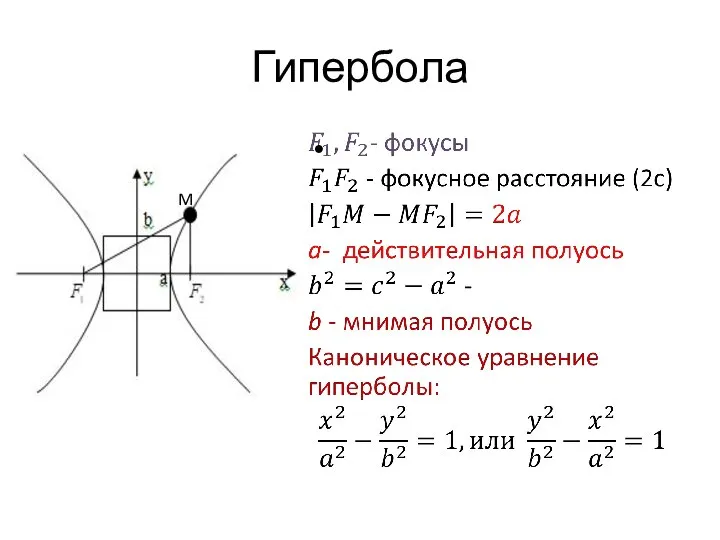
- 14. Гипербола M
- 17. Алгоритм построения гиперболы
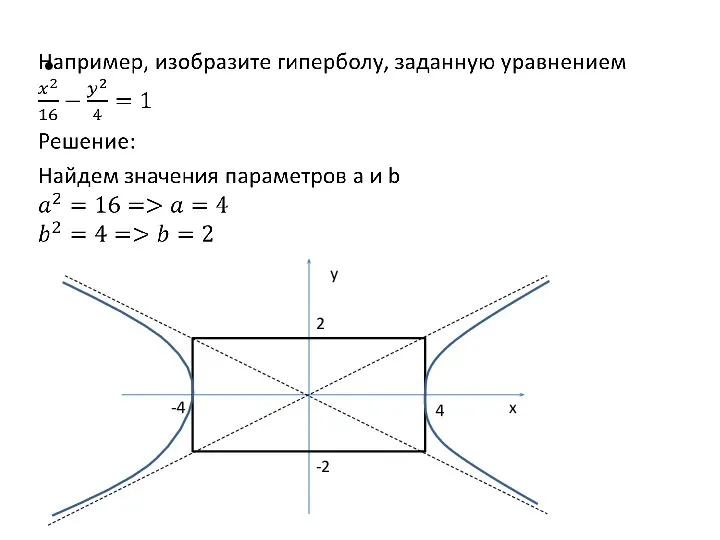
- 18. y x 4 -4 2 -2
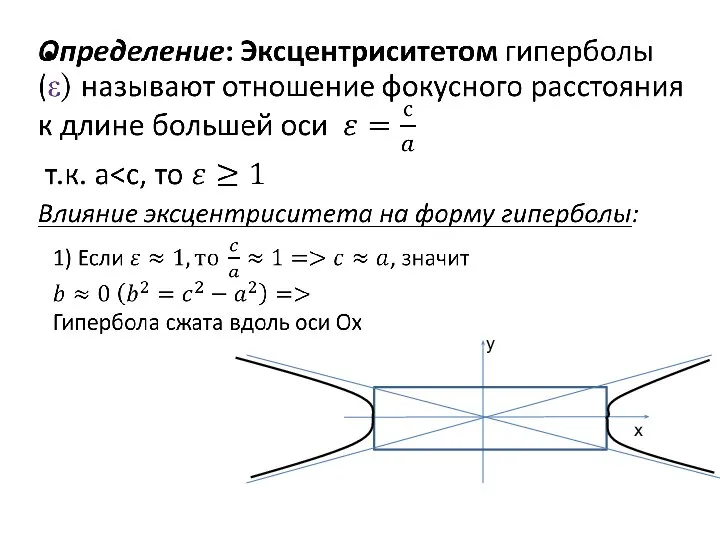
- 19. у х
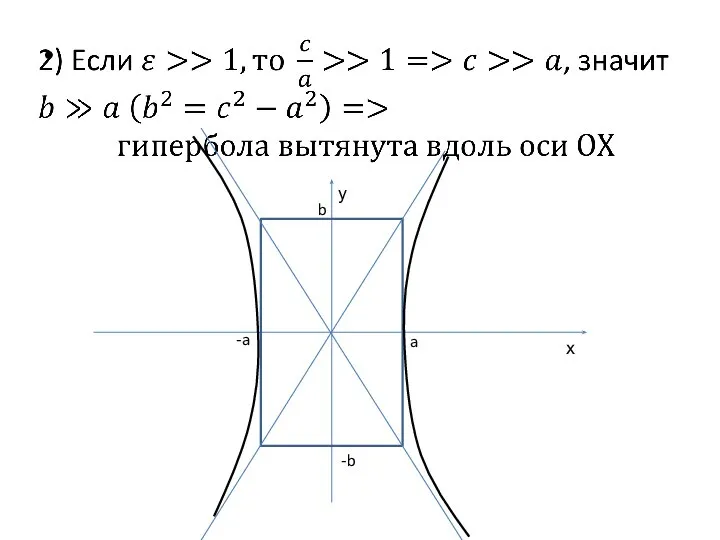
- 20. х у a -a b -b
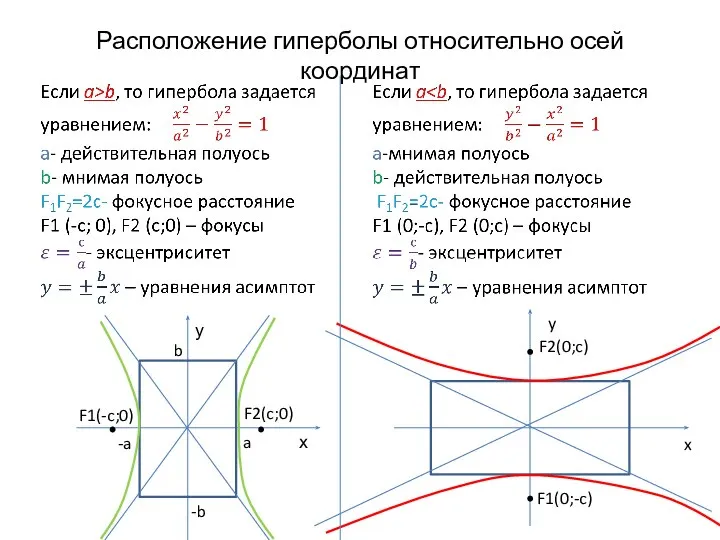
- 21. Расположение гиперболы относительно осей координат у х a -a b -b F2(c;0) F1(-c;0) x y F2(0;c)
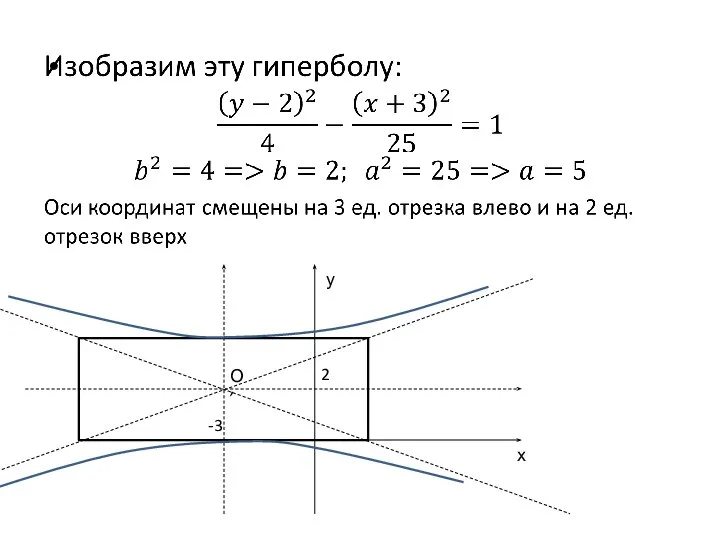
- 23. -3 2 х у О’
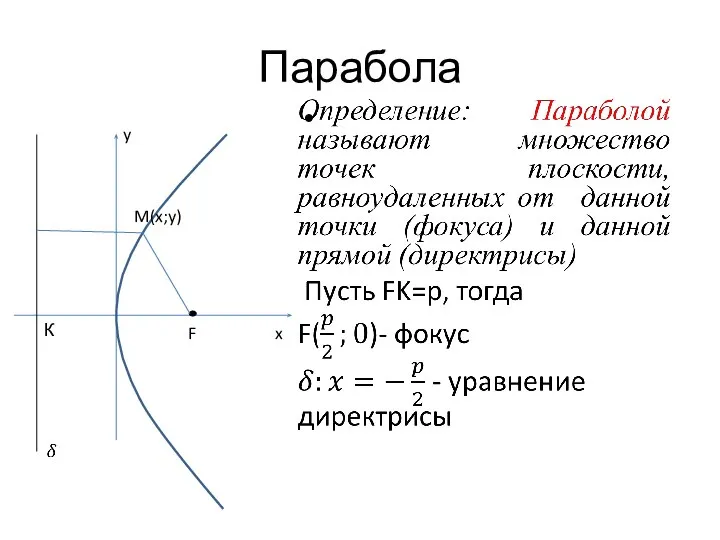
- 24. Парабола x y F M(x;y) К
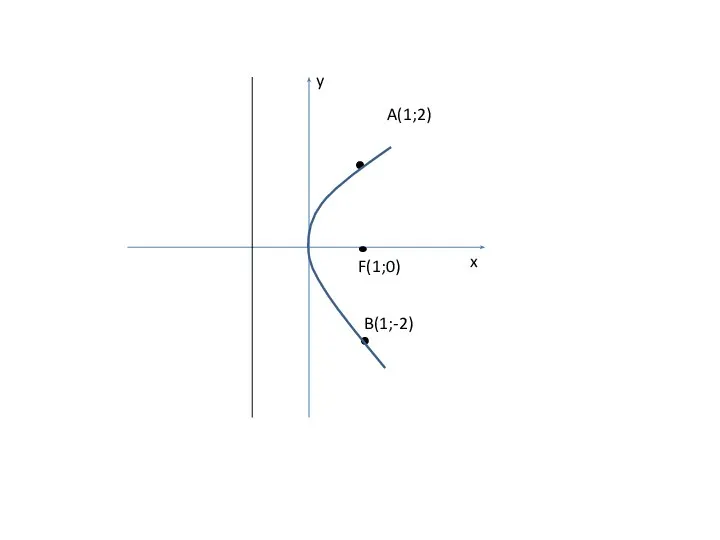
- 26. x y F(1;0) A(1;2) B(1;-2)
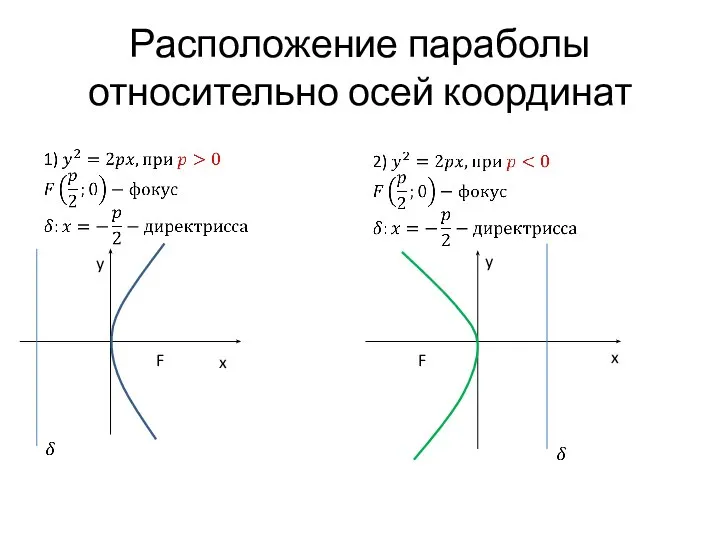
- 27. Расположение параболы относительно осей координат F x y F x y
- 29. Скачать презентацию















 Рождество в разных странах. Традиции
Рождество в разных странах. Традиции Электронная торговая площадка Грузовые перевозки - новая реальность грузовых железнодорожных перевозок
Электронная торговая площадка Грузовые перевозки - новая реальность грузовых железнодорожных перевозок Система взаимодействия с исполнительной и законодательной властью в рамках Программы увеличения потребления минеральных удобре
Система взаимодействия с исполнительной и законодательной властью в рамках Программы увеличения потребления минеральных удобре ПРЕЗЕНТАЦИЯ «Получение первичных профессиональных навыков и умений»
ПРЕЗЕНТАЦИЯ «Получение первичных профессиональных навыков и умений» Презентация на тему АНТРОПОГЕННОЕ ЗАГРЯЗНЕНИЕ ПРИРОДНОЙ СРЕДЫ ФАРМПОЛЛЮТАНТЫ
Презентация на тему АНТРОПОГЕННОЕ ЗАГРЯЗНЕНИЕ ПРИРОДНОЙ СРЕДЫ ФАРМПОЛЛЮТАНТЫ  Экосистема озера
Экосистема озера Реактивное движение
Реактивное движение Хватит слов вокруг социальных медиа. Дайте результат! - презентация
Хватит слов вокруг социальных медиа. Дайте результат! - презентация Стандарты оформления. Документ будет выполнен в стандартной программе Microsoft Word
Стандарты оформления. Документ будет выполнен в стандартной программе Microsoft Word Теоретическая и интегральная подготовка спортсменов
Теоретическая и интегральная подготовка спортсменов  Новый формат ежемесячного мониторинга ДОО в АСИОУ
Новый формат ежемесячного мониторинга ДОО в АСИОУ Методическое мастерство преподавателя ИЯ
Методическое мастерство преподавателя ИЯ Мир эмоций
Мир эмоций Презентация на тему Качество непродовольственных товаров
Презентация на тему Качество непродовольственных товаров  Мезенская роспись
Мезенская роспись Анализ финансоваых результатов деятельности организации
Анализ финансоваых результатов деятельности организации Географическая оболочка
Географическая оболочка  Презентация на тему Литературное чтение
Презентация на тему Литературное чтение  Россия – наша Родина
Россия – наша Родина Токарные инструменты
Токарные инструменты Архитектура Саратова
Архитектура Саратова Анализ финансового состояния предприятия
Анализ финансового состояния предприятия Вышли мыши
Вышли мыши Правовые основы системы налогов и сборов
Правовые основы системы налогов и сборов Создание и организация деятельности малого предприятия
Создание и организация деятельности малого предприятия Владимир Владимирович Маяковский 1893-1930
Владимир Владимирович Маяковский 1893-1930 Генетика человека Элективный курс для учащихся 9 класса
Генетика человека Элективный курс для учащихся 9 класса Концентрационные лагеря немецких фашистов
Концентрационные лагеря немецких фашистов