Теорема Котельникова

Теорема отсчетов
В 1933 году В.А. Котельниковым доказана теорема отсчетов, имеющая важное значение в теории связи: непрерывный сигнал с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам , взятым через интервалы , где F– верхняя частота спектра сигнала.

Ряд Котельникова
В соответствии с этой теоремой сигнал можно представить рядом Котельникова

Сигнал
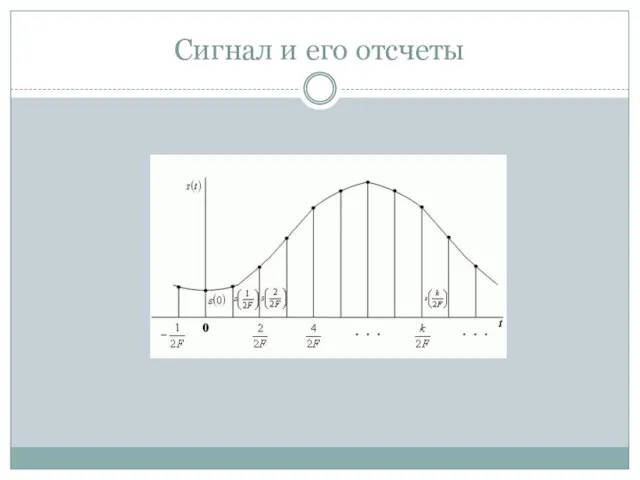
Таким образом, сигнал , можно абсолютно точно представить с помощью последовательности отсчетов , заданных в дискретных точках

Сигнал и его отсчеты

Функции
Функции образуют ортогональный базис в пространстве сигналов, характеризующихся ограниченным спектром.
,если (при )

Диапазон частот
Обычно для реальных сигналов можно указать диапазон частот, в пределах которого сосредоточена основная часть его энергии и которым определяется ширина спектра сигнала. В ряде случаев спектр сознательно сокращают. Это обусловлено тем, что аппаратура и линия связи должны иметь минимальную полосу частот. Сокращение спектра выполняют, исходя из допустимых искажений сигнала. Например, при телефонной связи хорошая разборчивость речи и узнаваемость абонента обеспечиваются при передаче сигналов в полосе частот

Функция отсчетов
Функция
вида называется
функцией отсчетов
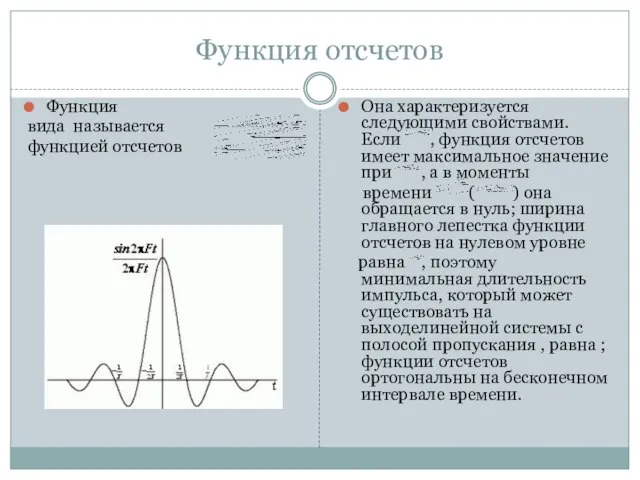
Она характеризуется следующими свойствами. Если , функция отсчетов имеет максимальное значение при , а в моменты
времени ( ) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне
равна , поэтому минимальная длительность импульса, который может существовать на выходелинейной системы с полосой пропускания , равна ; функции отсчетов ортогональны на бесконечном интервале времени.

Способ дискретной передачи
На основании теоремы Котельникова может быть предложен следующий способ дискретной передачи непрерывных сигналов:
Для передачи непрерывного сигнала по каналу связи с полосой пропускания определим мгновенные значения сигнала в дискретные моменты времени , ( ). После этого передадим эти значения по каналу связи каким - либо из возможных способов и восстановим на приемной стороне переданные отсчеты. Для преобразования потока импульсных отсчетов в непрерывную функцию пропустим их через идеальный ФНЧ с граничной частотой

Энергия сигнала
Можно показать, что энергия сигнала находится по формуле :
Выражение 1 :
Для сигнала, ограниченного во времени, выражение (1) преобразуется к виду:
Выражение 2:
Выражение (2) широко применяется в теории помехоустойчивого приема сигналов, но является приближенным, т.к. сигналы не могут быть одновременно ограничены по частоте и времени.