Л.37 (29) Колебания

2
6. Дифференциальное уравнение свободных гармонических колебаний и его решение
Динамическое уравнение
Кинематическое уравнение
Решение – закон косинуса
СЧ ГО
Амплитуда и начальная фаза определяются НУ

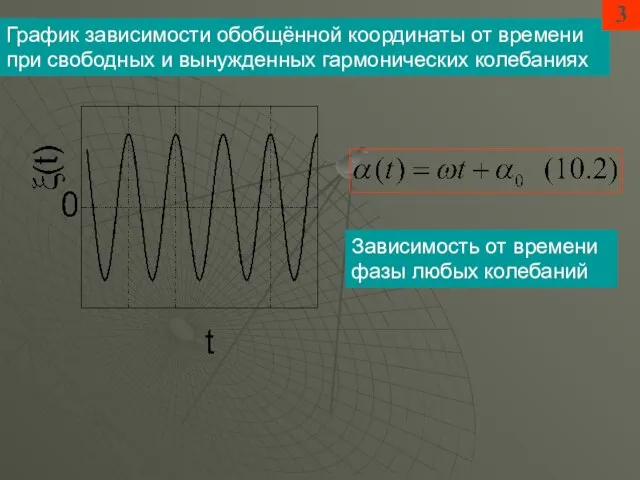
График зависимости обобщённой координаты от времени при свободных и вынужденных гармонических колебаниях
Зависимость от времени
фазы любых колебаний
3

4
7. Дифференциальное уравнение затухающих колебаний и его решение
Динамическое уравнение
Кинематическое уравнение
Решение – закон, по которому совершаются ЗК
Коэффициент затухания
Начальная амплитуда и начальная фаза определяются НУ

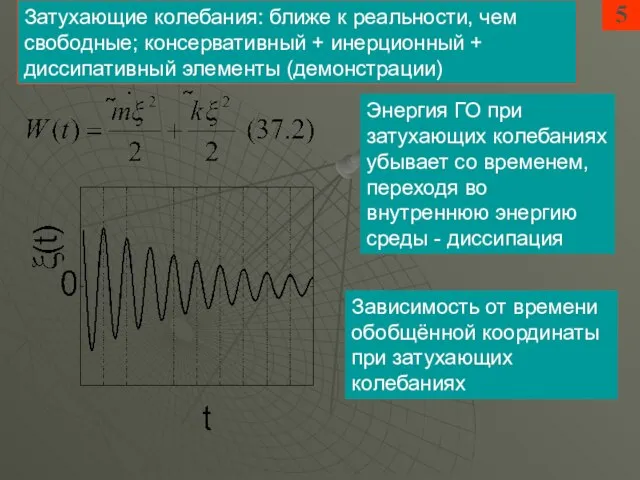
5
Затухающие колебания: ближе к реальности, чем свободные; консервативный + инерционный + диссипативный элементы (демонстрации)
Энергия ГО при затухающих колебаниях убывает со временем, переходя во внутреннюю энергию среды - диссипация
Зависимость от времени
обобщённой координаты при затухающих колебаниях

Практически наиболее интересны слабозатухающие колебания
6
Коэффициент затухания много меньше собственной частоты
Убыль энергии за один период много меньше энергии осциллятора в данный момент
Время релаксации много больше периода колебаний

Логарифмический декремент затухания (ЛДЗ) и добротность – удобные безразмерные характеристики диссипативных свойств осциллятора
7
Определение ЛДЗ
Определение добротности
Связь ЛДЗ с коэффициентом затухания и периодом
Связь ЛДЗ с добротностью

10
8. Дифференциальное уравнение вынужденных колебаний и его решение
Дифференциальное уравнение ВК
Решение – закон ВК
Амплитуда ВК (АЧХ)
Разность фаз ВВС и ВК (ФЧХ)

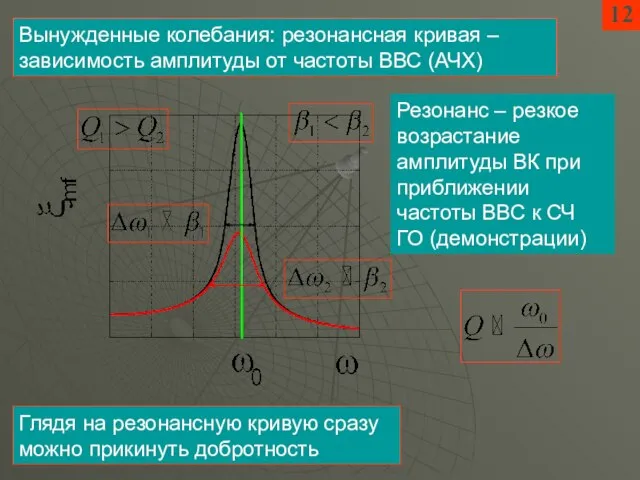
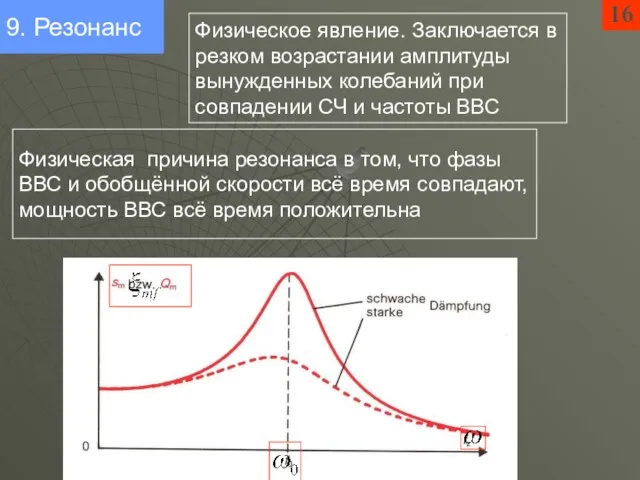
12
Вынужденные колебания: резонансная кривая – зависимость амплитуды от частоты ВВС (АЧХ)
Резонанс – резкое возрастание амплитуды ВК при приближении частоты ВВС к СЧ ГО (демонстрации)
Глядя на резонансную кривую сразу можно прикинуть добротность

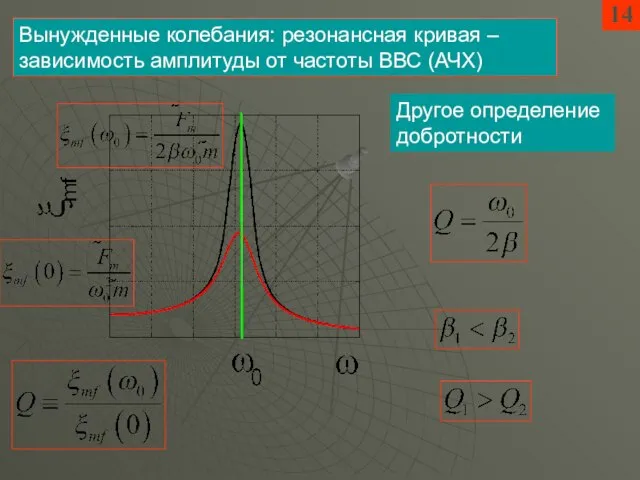
14
Вынужденные колебания: резонансная кривая – зависимость амплитуды от частоты ВВС (АЧХ)
Другое определение добротности

16
9. Резонанс
Физическое явление. Заключается в резком возрастании амплитуды вынужденных колебаний при совпадении СЧ и частоты ВВС
Физическая причина резонанса в том, что фазы ВВС и обобщённой скорости всё время совпадают, мощность ВВС всё время положительна

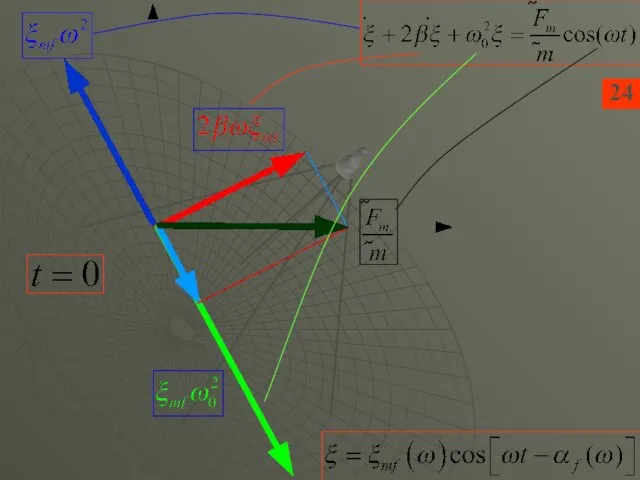
18
Метод векторных диаграмм позволяет наглядно и эффективно анализировать колебания:
анимация из Открытой физики
как бы катет, если - гипотенуза
тоже как бы катет, если - гипотенуза
Это мотивация использования «как бы» векторов для анализа колебательных процессов

Рецепт построения векторных диаграмм
Каждое слагаемое-колебание - стрелка
Амплитуда колебания – длина стрелки
Фаза колебания – угол между положительным направлением горизонтальной оси и стрелкой, положительный – против часовой стрелки
22

24

Векторная диаграмма вынужденных колебаний для случая резонанса
26