Содержание
- 2. Энергия – количественная мера движения материи в различных формах этого движения. С различными формами движения материи
- 3. Прямолинейное движение скалярная величина. Работа S α
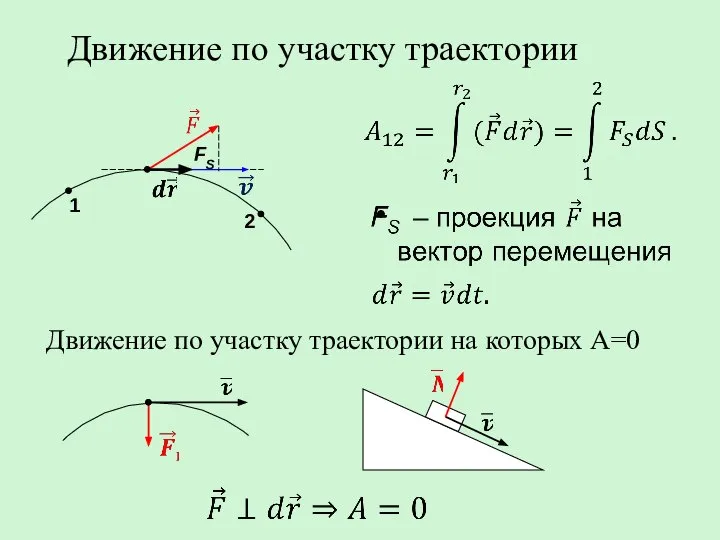
- 4. Движение по участку траектории FS 1 2 Движение по участку траектории на которых A=0
- 5. При графическом изображении FS(S) работа равна площади под кривой. Система СИ: [А] = джоуль, Дж. 1
- 6. Мощность (механизма или машины) – работа, совершаемая за единицу времени. Характеризует скорость совершения работы. Скалярная величина.
- 7. Кинетическая энергия механической системы – энергия механического движения этой системы. Сила вызывает движение тел и совершает
- 10. Использовался второй закон Ньютона, т.е. движение в ИСО. В разных ИСО, движущихся относительно друг друга, скорость
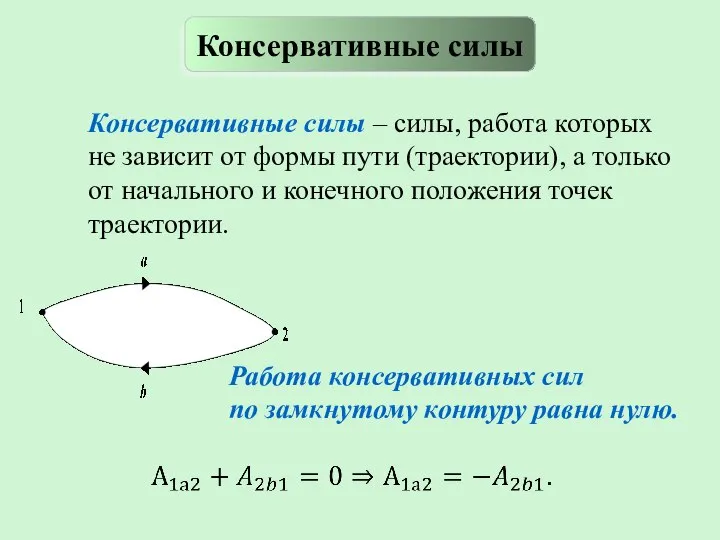
- 11. Консервативные силы – силы, работа которых не зависит от формы пути (траектории), а только от начального
- 12. Примеры консервативных сил (силовых полей):
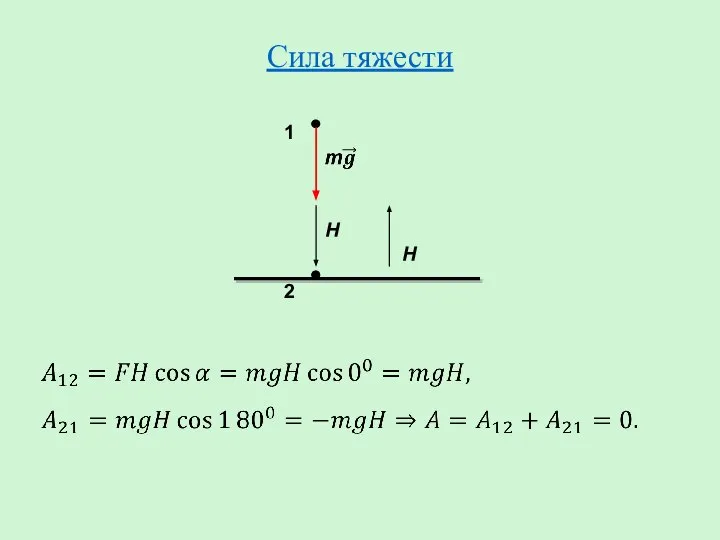
- 13. Сила тяжести
- 14. Сила упругости В одномерном случае F(x) Работа зависит от начального и конечного положения (x1; x2). Если
- 15. Диссипативные силы – силы, работа которых зависит от траектории перемещения тел. Пример: сила трения.
- 16. Потенциальная энергия – энергия системы тел, зависящая от взаимного расположения или их составных частей. Взаимодействие тел
- 17. Тело, находящееся в потенциальном поле другого тела, обладает потенциальной энергией.
- 18. Рассмотрим поле консервативных сил. Пусть перемещаем материальную точку из точки 1 в точку 2. При перемещении
- 19. Работа консервативны сил равна изменению потенциальной энергии, взятому с противоположным знаком. Выражения (8), (9) справедливы как
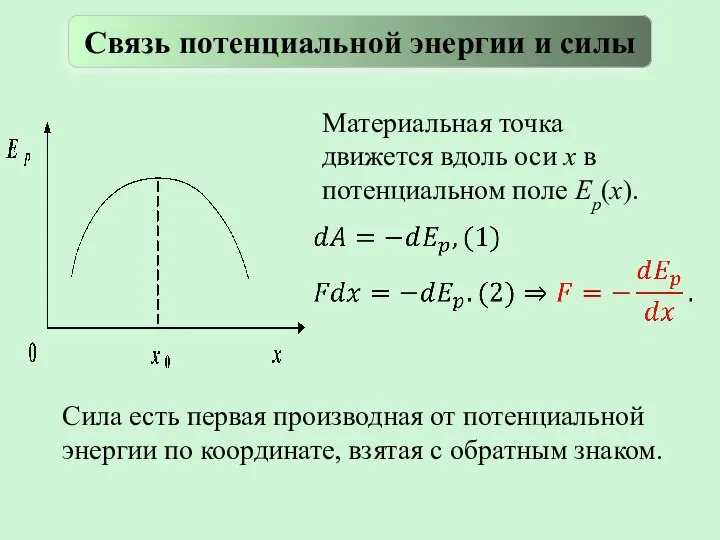
- 20. Материальная точка движется вдоль оси х в потенциальном поле Ep(x). Сила есть первая производная от потенциальной
- 21. В общем случае трехмерного пространства: В векторном виде:
- 22. Уравнение (2) в общем виде: Т.е. Ep определяется с точностью до С, но это не влияет
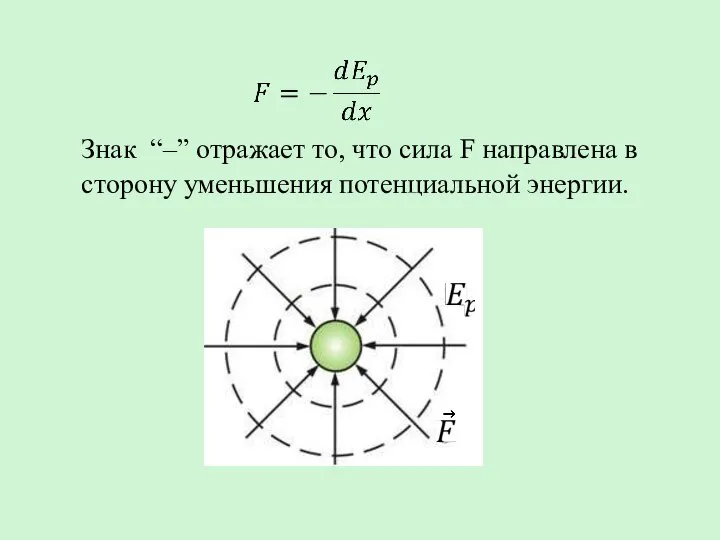
- 23. Знак “–” отражает то, что сила F направлена в сторону уменьшения потенциальной энергии.
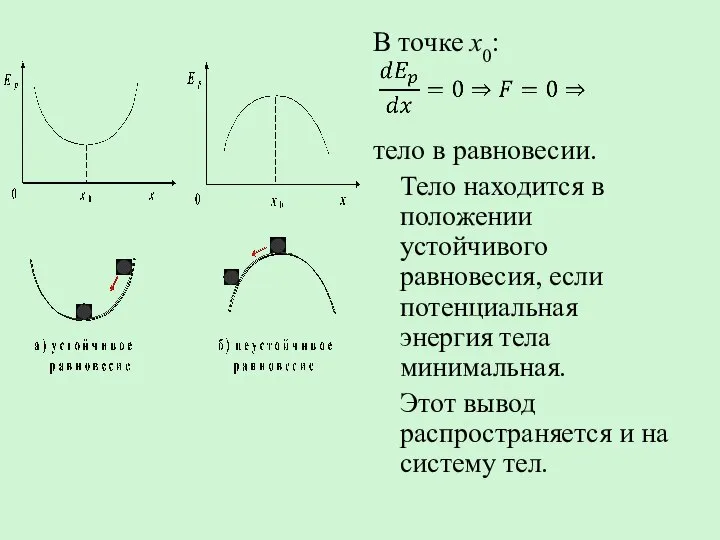
- 24. В точке х0: тело в равновесии. Тело находится в положении устойчивого равновесия, если потенциальная энергия тела
- 25. Потенциальное поле – поле консервативных сил.
- 26. Полная механическая энергия материальной точки (тела, частицы), находящейся в потенциальном поле (в консервативной системе), есть величина
- 27. Одномерное движение тела (материальной точки). В этом случае Ер является функцией лишь одной переменной (например, координаты
- 28. Рассмотрим консервативную систему, т.е. систему, в которой превращение механической энергии в другие виды отсутствует. В ней
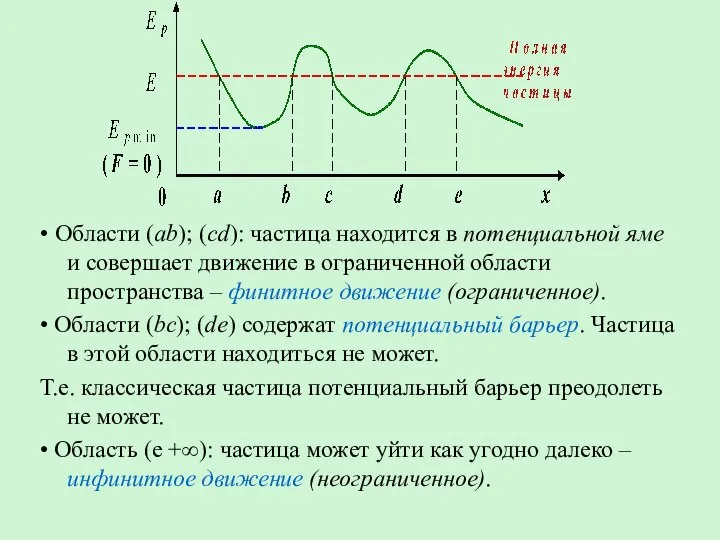
- 29. • Области (ab); (cd): частица находится в потенциальной яме и совершает движение в ограниченной области пространства
- 30. Закон сохранения энергии в механике
- 31. Второй закон Ньютона для i точки: Под действием силы точка за время dt совершает перемещение dri:
- 32. Суммируя по всем точкам, получаем: При переходе системы из одного состояния в другое: работа, совершаемая внешними
- 33. Если внешние неконсервативные силы отсутствуют, т.е. Полная механическая энергия консервативной системы есть величина постоянная, с течением
- 34. Замкнутая система – частный случай. В этом случае внешние силы не рассматриваются, т.е. – полная механическая
- 35. Наряду с консервативными силами в системе могут существовать неконсервативные силы (диссипативные, например, Fтр). В этом случае
- 36. Закон сохранения энергии в механике является частным случаем фундаментального (всеобщего) закона сохранения энергии: сумма всех видов
- 37. Удар – кратковременное взаимодействие двух или более тел. Центральный удар (двух шаров) – удар, при котором
- 38. Сила взаимодействия при ударе тел велика следовательно, внешними силами, действующими на тело, можно пренебречь. Поэтому систему
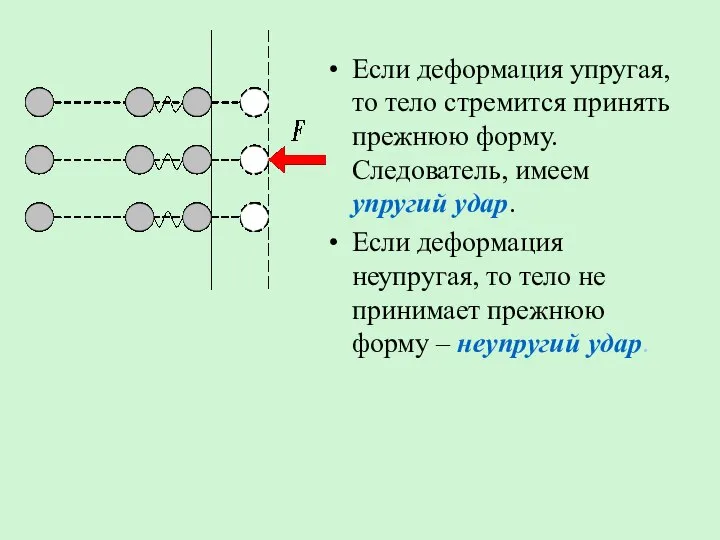
- 39. Если деформация упругая, то тело стремится принять прежнюю форму. Следователь, имеем упругий удар. Если деформация неупругая,
- 40. Во время удара происходит перераспределение энергии между соударяющимися телами. В общем случае относительная скорость тел после
- 41. Абсолютно упругий удар – удар, при котором внутренняя энергия соударяющихся тел не изменяется. Закон сохранения импульса:
- 44. При одинаковых массах происходит обмен скоростями.
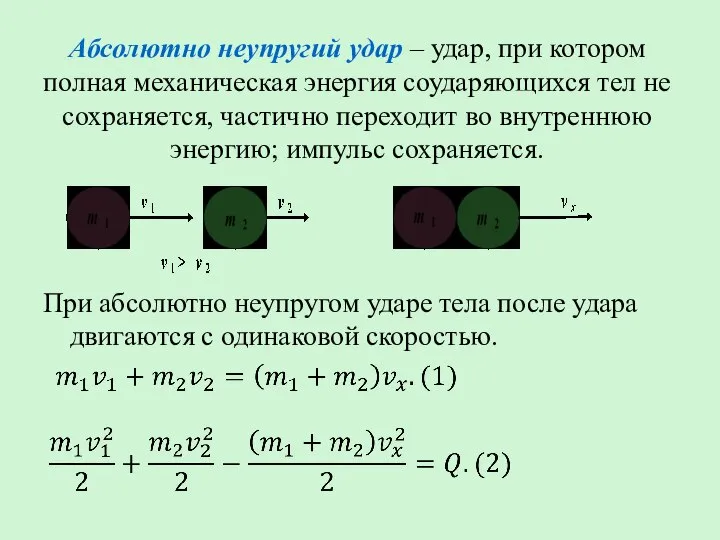
- 45. Абсолютно неупругий удар – удар, при котором полная механическая энергия соударяющихся тел не сохраняется, частично переходит
- 46. ● Наковальня Вся энергия переходит в теплоту или деформацию.
- 48. Скачать презентацию


![При графическом изображении FS(S) работа равна площади под кривой. Система СИ: [А]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183617/slide-4.jpg)




























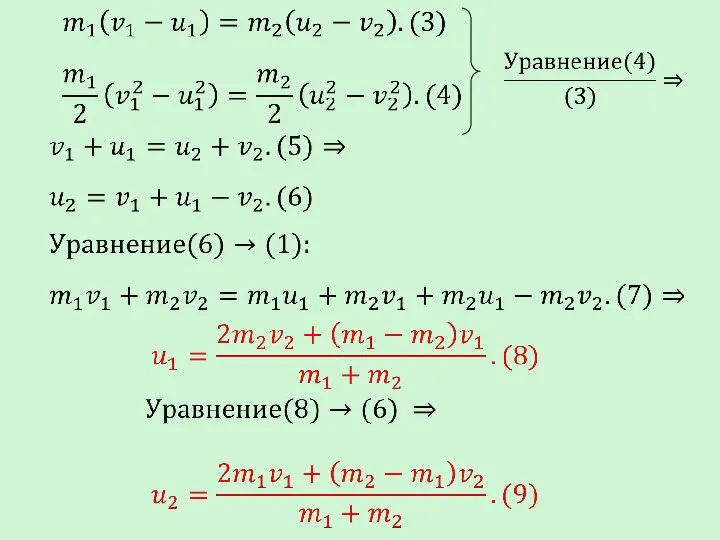
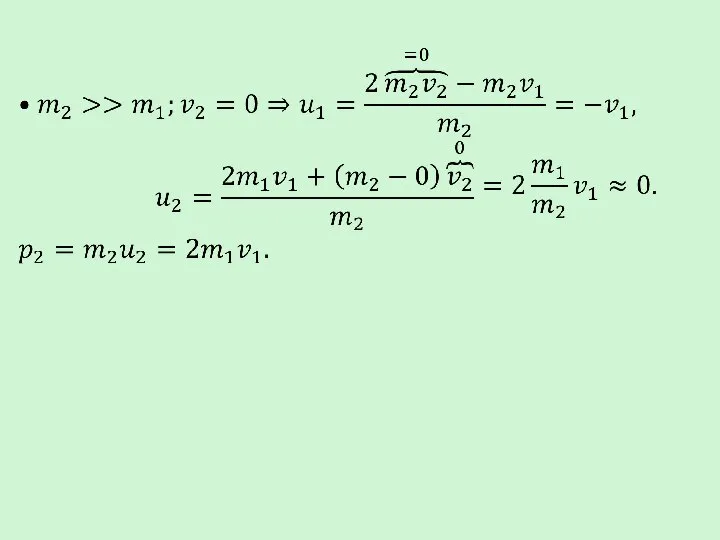


 Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк)
Денежные переводы физических лиц: состояние и тенденции развития (на примере ПАО Сбербанк) Особенности истории информатики
Особенности истории информатики Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты
Мотивирование топ-менеджеров в банковской сфере: подходы и инструменты = 1
= 1 Изустная среда мордовского села
Изустная среда мордовского села Показатели рыночной активности
Показатели рыночной активности Выхухоль. Красная книга
Выхухоль. Красная книга Обработка текстовой и графической информации. Создаём комбинированный документ
Обработка текстовой и графической информации. Создаём комбинированный документ Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год
Телевидение: я выбираю или меня выбирают. Автор и руководитель проекта: Симонова Ольга Владимировна 2004 год Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке
Что я сделаю, чтобы доверенный мне магазин стал лучшим на рынке Туалетная вода для мужчин Faberlic Intense
Туалетная вода для мужчин Faberlic Intense Межпроцедурные анализы и оптимизации
Межпроцедурные анализы и оптимизации Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны
Внешняя политика СССР в 1930-е гг. и накануне Великой Отечественной войны Урок 3 Человек и Бог в православии-повторение
Урок 3 Человек и Бог в православии-повторение 17 век
17 век ПЕРЕГОВОРЫ
ПЕРЕГОВОРЫ Изготовление вечернего платья
Изготовление вечернего платья Теорiя iгор
Теорiя iгор  Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс
Презентация на тему Роль гормонов в обмене веществ, росте и развитии организма биология 8 класс аня хочет санчо панчо
аня хочет санчо панчо Создание таблиц в Microsoft Word
Создание таблиц в Microsoft Word Teenagers’ society problems
Teenagers’ society problems Воля познавать
Воля познавать Любимое блюдо моей семьи
Любимое блюдо моей семьи Ладья. Урок №8
Ладья. Урок №8 Описательные характеристики распределения тестовых результатов
Описательные характеристики распределения тестовых результатов Презентация на тему Одиночество
Презентация на тему Одиночество Ich gehe mit meine Laterne
Ich gehe mit meine Laterne