Лекция

Логика высказываний оперирует простейшими высказываниями, которые могут быть или истинными, или ложными.
В разговорном языке встречаются более сложные повествовательные предложения, истинность которых может меняться при изменении объектов, о которых идет речь.

В логике такие предложения, истинность которых зависит от параметров, обозначают с помощью предикатов.
"Предикат" с английского переводится как сказуемое.

Определение предиката
Формально предикат - функция, аргументами которой могут быть ПРОИЗВОЛЬНЫЕ ОБ'ЕКТЫ из некоторого множества, а значения функции "истина" или "ложь".
Предикат можно рассматривать как расширение понятия высказывания.

Пример
"Маша любит кашу"
"Даша любит кашу"
"Саша любит кашу«
предикат "Икс любит кашу"
и вместо неизвестного Икс могут быть либо Маша, либо Даша, либо Саша.
Подстановка вместо Икс имени конкретного ребенка превращает предикат в обычное высказывание.

Определение
Предикат - это высказывание-функция, значение (истина/ложь) которого зависит от параметров

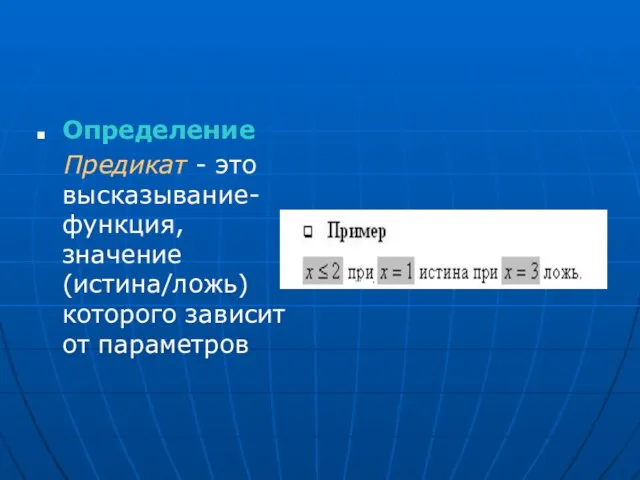
Определение
Одноместным предикатом Р(x) -произвольная функция переменного x, определенная на множестве M и принимающая значение из множества {1; 0}.
"ВСЕ любят Игрека" - одноместный предикат.
Замечание
Высказывания – это 0(нуль)-местный предикат,
булева функция – n-местный предикат.
"ВСЕ любят КОЙ-КОГО [некоторого]" - нульместный предикат, то есть высказывание.

Определение
Двухместный предикат Р(x,y) - функция двух переменных x и y, определенная на множестве М=М1хМ2 и принимающая значения из множества {1;0}.
Пример
Q(x, y) – “x=y” - предикат равенства на множестве RхR=R2
"Икс любит Игрека" -двухместный предикат.

Определение
n-местный предикат - это функция определенная на наборах длины n элементов некоторого множества M, принимающая значения в области True, False.
Множество М называется предметной областью предиката,
а x1, x2, ..xn –предметными переменными

Определение.
Предикат называется тождественно истинным (тождественно ложным), если на всех наборах своих переменных принимает значение 1 (0), выполнимым, если на некотором наборе своих переменных принимает значение 1

Логические операции над предикатами
Замечание
Предикаты при подстановки переменных становятся высказываниями, поэтому с предикатами можно производить все логические операции
Для предикатов справедливы логические операции и две новые операции, специфические.
- операциями навешивания кванторов или операциями квантификации.
Эти операции соответствуют фразам
"для всех" - квантор общности и "некоторые" - квантор существования.
Выражение "существует точно одно Х такое, что..." - квантор существования и единственности

Пример (Экзюпери)
"Ты любишь потому, что ты любишь.
Не существует причин, чтобы любить."
можно записать в виде:

Определение
Присоединение квантора с переменной к предикатной формуле называется навешивание квантора на переменную х.
Переменная при этом называется связанной и вместо нее подставлять константы уже нельзя.
Если квантор навешивается на формулу с несколькими переменными, то он уменьшает число несвязанных переменных в этой формуле

Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М),
в высказывании же х называют связанной квантором всеобщности.

Переменная , на которую навешивается квантор называется связанной.
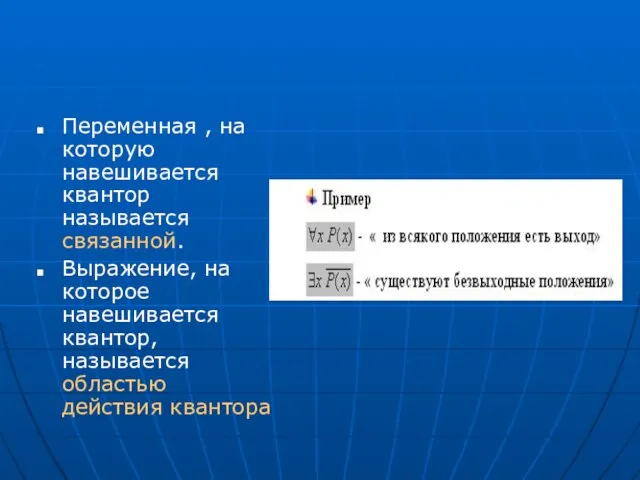
Выражение, на которое навешивается квантор, называется областью действия квантора

Пример
Предикат "ВСЕ любят кашу":
Возьмем отрицание
"НЕ ВЕРНО, что ВСЕ любят кашу".
Это равносильно (по закону Де Моргана!) заявлению:
"НЕКОТОРЫЕ НЕ любят кашу.
отрицание "задвинули" за квантор, в результате чего квантор сменился на противоположный

Кванторы общности и существования называют двойственными относительно друг друга.
Вот некоторые "классические примеры"несоответствия языка предикатов и естественного языка

Пример
предикат
"Собакам и кошкам вход воспрещен".
"ДЛЯ ВСЕХ иксов справедливо:
ЕСЛИ икс - собака И икс - кошка, ТО иксу вход запрещен"
Ясно что таких иксов, которые бы были одновременно собакой и кошкой не существует! Как, впрочем, и таких игреков.
Поэтому ЕСЛИ икс - собака ИЛИ икс - кошка, ТО иксу вход запрещен"

Пример

Свойства кванторов
1. Коммутативность одноименных кванторов
2.
Перестановка кванторов общности и существования меняет смысл.

Основные законы, содержащие кванторы

Равносильные формулы логики предикатов
Определение
Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Правила переноса кванторов через отрицание или
законы де Моргана для кванторов
Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, не содержащая х).
Тогда имеют место равносильности

Правила переноса кванторов через отрицание или
законы де Моргана для кванторов

«квантор можно вносить и выносить за скобки в конъюнкции»

постоянное высказывание можно вносить под знак квантора всеобщности и выносить из под знака в конъюнкции, дизъюнкции и импликации

квантор существования можно вносить и выносить за скобки в дизъюнкции»

Нормальные формы формул логики предикатов
В логике предикатов формулы могут иметь нормальную форму.
При этом, используя равносильности логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме.
В логике предикатов различают два вида нормальных форм: приведенную и предваренную

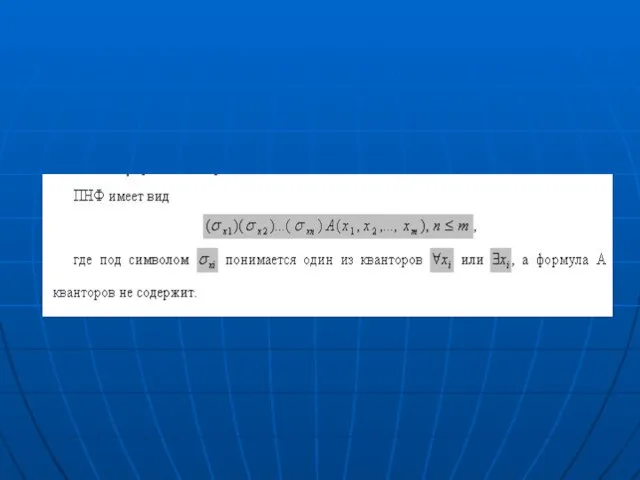
Среди нормальных форм формул логики предикатов выделяют так называемую предваренную (префиксную) нормальную форму (ПНФ).
В ней кванторные операции
либо полностью отсутствуют,
либо они используются после всех операций алгебры логики

Пример
Получили приведенную нормальную форму исходной формулы.

Алгоритм получения (приведения) ПНФ.
Формула B называется предваренной нормальной формой формулы A ,
если она удовлетворяет ниже перечисленным требованиям:
1. Формулы А и B равносильны.
2. Формула B удовлетворяет следующим условиям:
а) используются логические операции ┐, v , & , при этом отрицание применяется только в атомарных формулах;
б) операции кванторов следуют за операциями алгебры ┐, v , &

Шаг 1. Исключить связки эквивалентности (~) и импликации (→).
Формула x ~ у заменяется на (x → у) & (x → у), а формула
A → B заменяется на (Ā v B).
Шаг 2. Переименовать, если необходимо, связанные переменные таким образом, чтобы никакая переменная не имела бы одновременно свободных и связанных вхождений. Это условие рассматривается и по отношению к подформулам.

Шаг 3. Удалить те квантификации, область действия которых не содержит вхождений квантифицированной переменной.
Шаг 4. Перенести отрицания внутри формулы в соответствия со следующими правилами:
Шаг 5. Перенести все квантификации в начало формулы

Скулемовские функции
Приведение формулы ЛП к сколемовской форме (сколемизация) призвано обеспечить дальнейшее упрощение логических представлений и облегчить введение процедур машинной обработки в ЛП.
Отправной точкой сколемизации является предваренная нормальная форма, матрица которой приведена к конъюнктивной нормальной форме (КНФ).
Цель сколемизации - исключение Ǝ- квантификаций

Алгоритм получения сколемовской формы
сопоставить каждой Ǝ- квантифицированной переменной список ∀- квантифицированных переменных, предшествующих ей,
а также некоторую еще не использованную функциональную константу, число мест, у которой равно мощности списка.
Данная константа будет представлять сколемовскую функцию;

4) в матрице формулы заменить каждое вхождение каждой Ǝ- квантифицированной переменной на некоторый терм.
Этот терм является функциональной константой, соответствующей данной переменной и снабженной списком аргументов, также соответствующим той же самой переменной;
5) устранить из формулы все Ǝ - квантафикации.