Момент образования трещин в изгибаемых элементах по способу ядровых моментов

Расчет изгибаемых, внецентренно сжатых, а также внецентренно растянутых элементов по образованию трещин производится из условия:
Где момент внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно оси, параллельной нулевой линии и проходящей через ядровую точку, наиболее удаленную от растянутой зоны, трещинообразование которой проверяется

момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин и опреде­ляемый по формуле:
где Мrp — момент усилия Р относительно той же оси, что и для определения Мr; знак момента определяется направлением вращения., т.е.
упругопластический момент сопротивления железобетонного сечения по растянутой зоне в предположении, что продольная сила отсутствует;
эксцентриситет усилия обжатия относительно центра тяжести приведенного сечения;
r - расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести приведенного сечения.

1. Ширина раскрытия трещин, нормальных к оси элементов
Расчет по раскрытию трещин.
Ширина раскрытия трещин, нормальных к продольной оси элемента, представляет собой разность удлинений арматуры и растянутого бетона на участке между трещинами длиной , т.е.
Средней деформацией растянутого бетона как величиной малой в сравнении со средней деформацией растянутой арматуры обычно пренебрегают и принимают
или

Ширину раскрытия трещин, нормальных к продольной оси элемента acrc, мм определяют по формуле 144 СНиП 2.03.01-84*.
где δ - коэффициент, учитывающий напряженное состояние элемента;
ϕl ⎯ коэффициент, учитывающий длительность действия нагрузки;
— коэффициент, зависящий от вида и профиля продольной
растянутой арматуры;
σs — напряжение в продольной арматуре или приращение напряжений
после погашения обжатия в растянутой арматуре;
— коэффициент армирования сечения;
d — диаметр арматуры, мм.

По СП 52-101-2003 по п.7.2.12 ширину раскрытия трещин, нормальных к продольной оси элемента acrc, мм определяют:

Шаг трещин определяется из условия разности усилий в арматуре в трещине и между трещинами силами сцепления:
где а – периметр арматурных стержней.
По п. 7.2.14 СП 52-101-2003 значение базового расстояния между трещинами определяют
, но

Существует 3 категории трещиностойкости:
1. трещины не допустимы;
2. трещины допустимы непродолжительные (acrc2) с последующим закрытием.
При сумме постоянной и длительно действующих нагрузок g+gдлит – трещин быть не должно, при добавлении к этой сумме кратковременной нагрузки gкрат – трещины открываются. Как только нагрузку gкрат убирают, трещины закрываются (склеиваются).
3. трещины допускаются непродолжительные (acrc2) и продолжительные (acrc1).
При сумме постоянной и длительно действующих нагрузок g+gдлит – трещин допускаются ограниченной ширины acrc1, при добавлении к этой сумме кратковременной нагрузки gкрат – образуются трещины acrc2

Расчет по закрытию трещин.
Закрытие трещин, нормальных и наклонных к продольной оси элемента, должно быть обеспечено в предварительно напряженных конструкциях, отвечающих требованиям 2-ой категории трещиностойкости. Это обусловлено тем, что для коррозии арматуры наиболее опасно продолжительное раскрытие трещин.
Для надежного закрытия трещин, нормальных к продольной оси элемента, должно соблюдаться 2 условия:
1. ,
где предварительное напряжение в арматуре с учетом всех потерь; приращение растягивающего напряжения в арматуре от действия внешних нагрузок.
2. сечение с трещиной в растянутой зоне при постоянной и длительной нагрузках должно оставаться обжатым с нормальными напряжениями на растягиваемой внешними нагрузками грани
.
Если нет преднапряжения, то расчет ведут по 3 категории трещиностойкости.

РАСЧЕТ ПО ДЕФОРМАЦИЯМ (ПРОГИБАМ)

1. Определение кривизны железобетонного элемента
Расчет перемещений железобетонных элементов – прогибов и углов поворота – связан с определением кривизны оси при изгибе или с определением жесткости элементов. По длине железобетонного элемента в зависимости от вида нагрузки и характера напряженного состояния могут быть участки без трещин (или участки, где трещины закрыты) и участки, где в растянутой зоне есть трещины. Элементы, или участки элементов не имеют трещин в растянутой зоне, если при действии постоянных, длительных и краковременных нагрузок с коэффициентом надежности по нагрузке трещины не образуются.

2. Определение прогибов
Для изгибаемых элементов при < 10 необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб ftot равен сумме прогибов, обусловленных соответственно деформацией изгиба fm и деформацией сдвига fq.
Прогиб fm, обусловленный деформацией изгиба, определяется по формуле (171) СНиП 2.03.01 –84*:
где изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;
полная кривизна элемента в сечении х от нагрузки, при которой
определяется прогиб; знак принимается в соответствии с эпюрой кривизны.

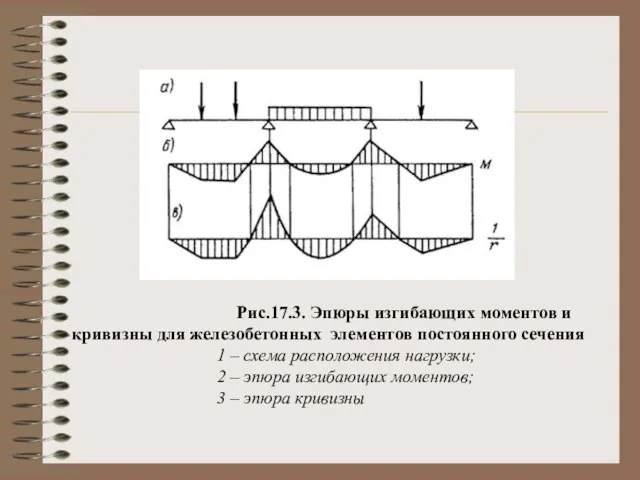
Рис.17.3. Эпюры изгибающих моментов и кривизны для железобетонных элементов постоянного сечения
1 – схема расположения нагрузки;
2 – эпюра изгибающих моментов;
3 – эпюра кривизны

Определение кривизны железобетонных элементов на участках без трещин в растянутой зоне.
На участках, где не образуются нормальные к продольной оси трещины, полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяется по формуле (155) СНиП 2.03.01-84*
где — кривизна от действия кратковременных нагрузок, определяемых согласно указаниям п. 1.12* СНиП 2.03.01-84*.
— кривизна от действия постоянных и длительных временных нагрузок (без учета усилия Р).

где М — момент от соответствующей внешней нагрузки (кратковременной, дли­тельной) относительно оси, нормаль­ной к плоскости действия изгибаю­щего момента и проходящей через центр тяжести приведенного сечения;
φb1 — коэффициент, учитывающий влияние кратковременной ползучести бетона.
φb2 — коэффициент, учитывающий влияние длительной ползучести бетона на де­формации элемента без трещин.
— кривизна, обусловленная выгибом элемента от кратковременного действия усилия предварительного обжатия Р
— кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия
здесь εb, ε’b — относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия и определяемые соответственно на уровне центра тяжести растянутой продольной арматуры и крайнего сжатого волокна бетона

σb – принимается численно равным сумме потерь предварительного напряжения от быстронатекающей ползучести, усадки бетона, т.е.
σ’b — принимается для напрягаемой арматуры на уровне край­него сжатого волокна бетона.
Для элементов без предварительного напряжения значения кривизны
принимают равными нулю.

Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне.
На участках, где образуются нормальные к продольной оси элемента трещины в стадии II ,общее деформированное состояние определяют средними деформациями растянутой арматуры , средними деформациями бетона сжатой зоны и средним положением нейтральной оси с радиусом кривизны r.
Из подобия треугольников на рисунке 17.2 получаем:

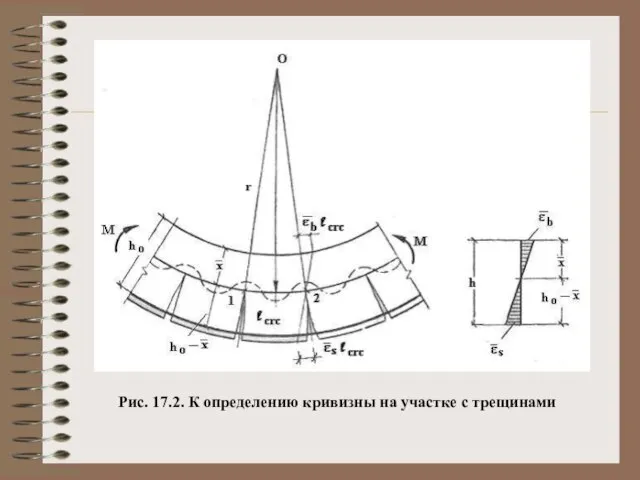
Рис. 17.2. К определению кривизны на участке с трещинами

следовательно
учитывая, что
, получаем:
Таким образом,

Учитывая свесы полок для таврового сечения коэффициентом ( ),
получаем:
В общем случае на участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также внецентренно растянутых при элементов прямоугольного, таврового и двутаврового (коробчатого) сечений должна определяться по формуле:
Ntot – равнодействующая продольной силы N и усилия предварительного обжатия Р (при внецентренном растяжении сила N принимается со знаком „минус").
Для элементов, выполняемых без предваритель­ного напряжения арматуры, усилие Р допускается принимать равным нулю.
Значение ξ вычисляется по формуле (161) СНиП 2.03.01 –84*.