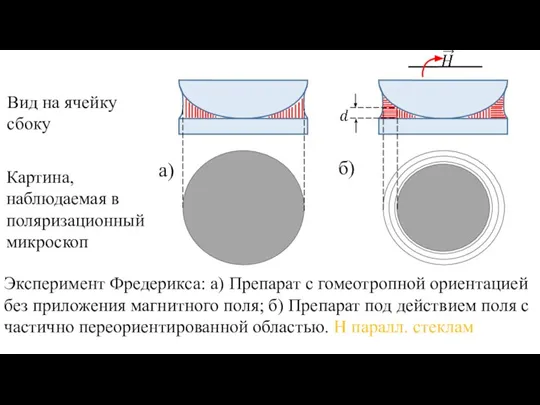
Lektsia_6

Эксперимент Фредерикса: а) Препарат с гомеотропной ориентацией без приложения магнитного поля; б) Препарат под действием поля с частично переориентированной областью. Н паралл. стеклам
Картина, наблюдаемая в поляризационный микроскоп
Вид на ячейку сбоку

Следствие из эксперимента Фредерикса:

Выражение для упругой энергии в случае сильного сцепления в одноконстантном приближении:
Уравнение Эйлера-Лагранжа в нашем случае будет иметь вид:

Выражение для магнитной когерентной длины:
Подставим (6-8) в (6-7) и преобразуем его. Получим:

Проинтегрируем (6-9):

Проинтегрируем полученной выражение еще раз:
Решая (6-12) имеем:

Выражение для упругой энергии в случае сильного сцепления в одноконстантном приближении:
Уравнение Эйлера-Лагранжа:

Проинтегрировав его, получим:
Считая, что при х=0 θ=θм, то для константы интегрирования С будем иметь:

Так как при х=0, θ=θм, можно записать:

Подставляя в (6-22) уравнение для когерентной длины волны (6-8) получим:
Или:

Магнитное поле не будет влиять на ориентацию нематика, если:
Тогда можно приближенно положить:
Подставим его в (6-8):

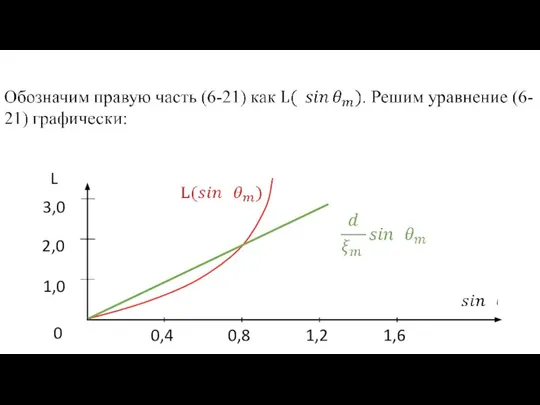
Сравнивая полученное уравнение с (6-8) имеем:
Подставим результат в (6-21):

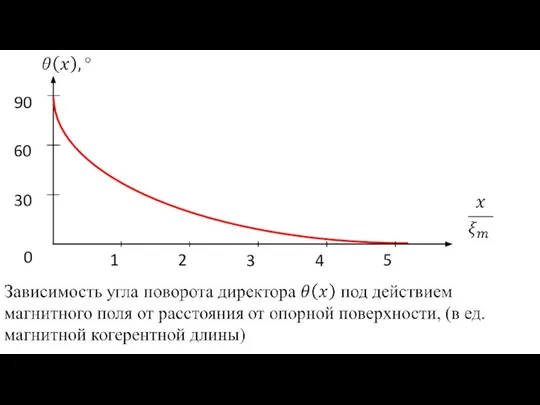
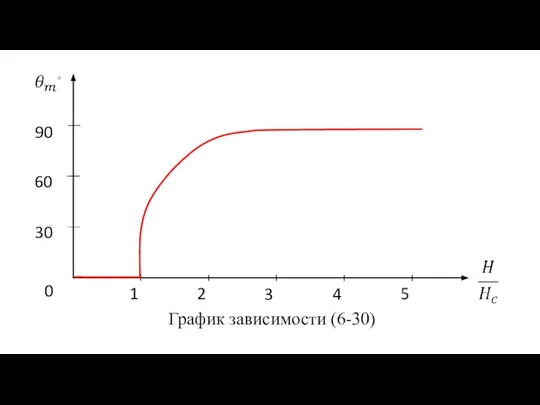
График зависимости (6-30)

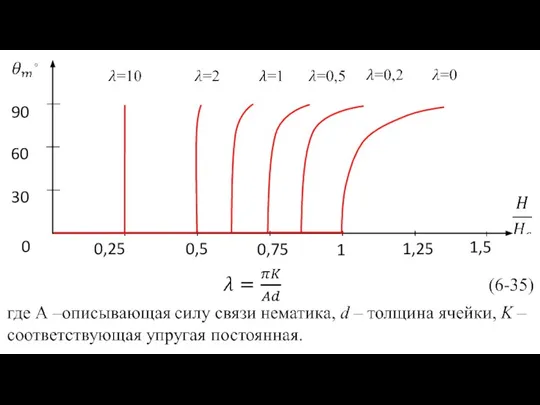
Подставим в уравнение (6-20) строгие выражения (6-8) и (6-23):
Заменим интеграл справа приближенным значением, получим:

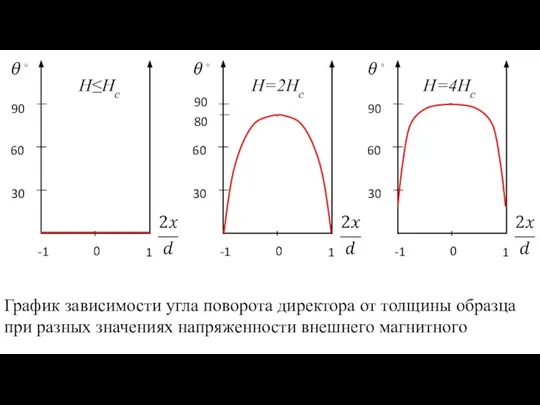
Н≤Hc
Н=2Hc
Н=4Hc
График зависимости угла поворота директора от толщины образца при разных значениях напряженности внешнего магнитного

Критическое поле для электрического перехода Фредерикса определяется аналогично с магнитным:
Тогда критическое напряжение для такого перехода: