Лекция 3

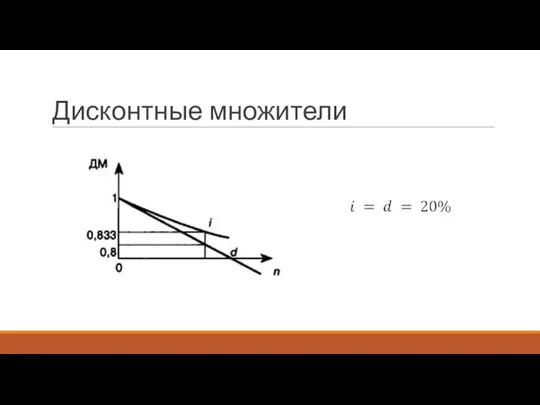
Дисконтирование
Термин “дисконтирование” употребляется и в более широком смысле — как средство определения любой стоимостной величины, относящейся к будущему, на более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному, моменту времени.
В зависимости от вида процентной ставки применяют два метода дисконтирования
математическое дисконтирование
банковский (коммерческий) учет.
В первом случае применяется ставка наращения, во втором — учетная ставка.

Математическое дисконтирование

Пример
Через 250 дней после подписания договора должник уплатит 546 тысяч тенге. Кредит выдан под 18% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?

Банковский учет (учет векселей)
Банк или другое финансовое учреждение до наступления срока платежа (date of maturity) по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, однако ранее указанного на нем срока.
При учете векселя применяется банковский, или коммерческий, учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока (maturity value). При этом применяется учетная ставка d.

Дисконтирование

Дисконтный множитель

Пример
Тратта (переводной вексель) выдан на сумму 1 млн тенге с уплатой 17.11.2020. Владелец векселя учел его в банке 23.09.2020 по учетной ставке 20%. Рассчитайте полученную при учете сумму

Наращение по учетной ставке

Пример
Вексель на сумму 1 млн тенге выдан с 20.01 по 05.10 включительно под 18% годовых (невисокосный год). Определить начисленную сумму при условии, что проценты начисляются по простой ставке дисконтирования d = 18%.

Прямые и обратные задачи при начислении процентов и дисконтировании по простым ставкам
Очевидно, что рассмотренные два метода наращения и дисконтирования — по ставке наращения i и учетной ставке d — приводят к разным результатам даже тогда, когда i = d.

Дисконтные множители

Срок ссуды

Пример
Какова должна быть продолжительность ссуды в днях для того, чтобы долг, равный 100 тыс. р уб ., вырос до 120 тыс. руб. при условии, что начисляются простые проценты по ставке 25% годовых? Рассчитайте используя точные проценты (K = 365 дней).

Величина процентной ставки

Пример
Договор предусматривает погашение обязательства в размере 110 тысяч тенге через 120 дней. Первоначальная сумма долга составляет 90 тысяч тенге (АСТ/360). Необходимо определить рентабельность ссудной операции для кредитора в виде процентной ставки и учетной ставки.

Процент скидки

Пример
Стороны договорились о том, что из суммы ссуды, выданной на 210 дней, удерживается дисконт в размере 12%. Необходимо определить цену кредита в виде годовой ставки простых процентов и учетной ставки (К = 360)

Конверсия валюты и наращение процентов

Пример
1) Предполагается разместить 1000 долларов на тенговом депозите. Курс продажи на начало срока депозита 424,9 тенге за 1 доллар, курс покупки доллара на конец операции 426,5 тенге. Процентные ставки: i = 22%; j = 15% (360/360). Срок вклада 3 месяца. Определить начисленную сумму в долларах и прямое увеличение исходной суммы в долларах.
2) Предполагается разместить на валютном депозите сумму в тенге (1 миллион). Остальные условия остаются. Определить начисленную сумму в тенге к концу срока и прямое вложение в тенговый депозит

Задача 1
7 февраля предприниматель обратился в банк за кредитом до 14 мая того же года по простой процентной ставке 18% годовых. Банк, удержав при выдаче кредита проценты за весь его срок, выдал предпринимателю 50 тысяч тенге. Какую сумму нужно будет вернуть в банк? (високосный год)

Задача 2
Компания обратилась в банк 1 марта за кредитом в 150 тысяч тенге, пообещав вернуть сумму с процентами в конце года. Какой способ начисления простых процентов выгоден предприятию и банку, если используется процентная ставка 26% годовых и год не високосный?

Задача 3
Банк выдал кредит в размере 1 млн тенге. В соглашении принята простая процентная ставка на первые шесть месяцев, равная 20% годовых, а каждые последующие 0,5 года ставка увеличивается на 3% по сравнению с предыдущей. Срок контракта 3 года. Определить начисленную сумму за весь срок действия договора.

Задача 4
Через какое время депозит в 50 тысяч тенге увеличится до 60 тысяч тенге при начислении процентов по простой процентной ставке 32% годовых?

Задача 5
Банк должен заплатить 70 тысяч тенге за использование в течение четырех месяцев 960 тысяч тенге. Определить стоимость привлеченных средств в виде простой годовой процентной ставки?

Задача 6
Банк выдал кредиты своим четырем клиентам A, B, C и D следующим образом: клиент A на 45 дней под 28% годовых; Все полученные от клиента А деньги я сразу отдал клиенту Б на 120 дней под 33% годовых; Всю полученную от клиента Б сумму я отдал клиенту С на 100 дней под 32% годовых и, получив деньги от клиента С, отдал клиенту Г на 40 дней под 30% годовых. Клиент Д по истечении срока вернул в банк 370 632 тенге. Сколько получил клиент А, если во всех случаях начислялись простые проценты?

Задача 7
По векселю, учитываемому за полтора года до погашения, уплачено 45 тыс. тенге по простой учетной ставке 12%. Определить номинальную стоимость векселя.