Слайд 26. Кривые линии
1, 2, 3 – характерные точки;
А – промежуточная точка;
t –
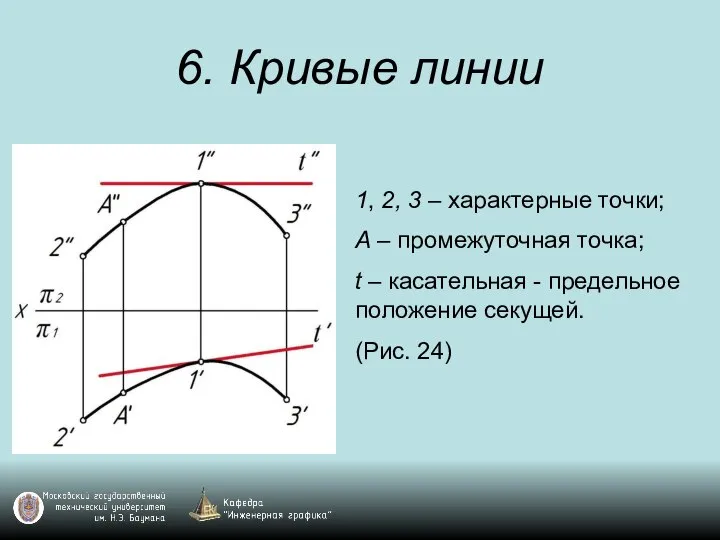
касательная - предельное положение секущей.
(Рис. 24)
Слайд 3Плоские кривые
Проекции окружности (рис. 25)

Слайд 4Плоские кривые
Проекции окружности (рис. 25)

Слайд 5Плоские кривые
Проекции окружности (рис. 25)

Слайд 6Плоские кривые
Проекции окружности (рис. 25)

Слайд 7Плоские кривые
Проекции окружности (рис. 25)

Слайд 8Плоские кривые
Проекции окружности (рис. 25)

Слайд 9Плоские кривые
Проекции окружности (рис. 25)

Слайд 10Плоские кривые
Проекции окружности (рис. 25)

Слайд 11Плоские кривые
Проекции окружности (рис. 25)

Слайд 12Плоские кривые
Проекции окружности (рис. 25)

Слайд 13Плоские кривые
Проекции окружности (рис. 25)

Слайд 14Плоские кривые
Проекции окружности (рис. 25)

Слайд 15Построение эллипса по двум осям (рис. 26)

Слайд 16Построение эллипса по двум осям (рис. 26)

Слайд 17Построение эллипса по двум осям (рис. 26)

Слайд 18Построение эллипса по двум осям (рис. 26)

Слайд 19Построение эллипса по двум осям (рис. 26)

Слайд 20Построение эллипса по двум осям (рис. 26)

Слайд 21Построение эллипса по двум осям (рис. 26)

Слайд 22Построение эллипса по двум осям (рис. 26)

Слайд 23Построение эллипса по двум осям (рис. 26)

Слайд 24Построение эллипса по двум осям (рис. 26)

Слайд 25Построение эллипса по двум осям (рис. 26)

Слайд 26Построение эллипса по двум осям (рис. 26)

Слайд 27Построение эллипса по двум осям (рис. 26)
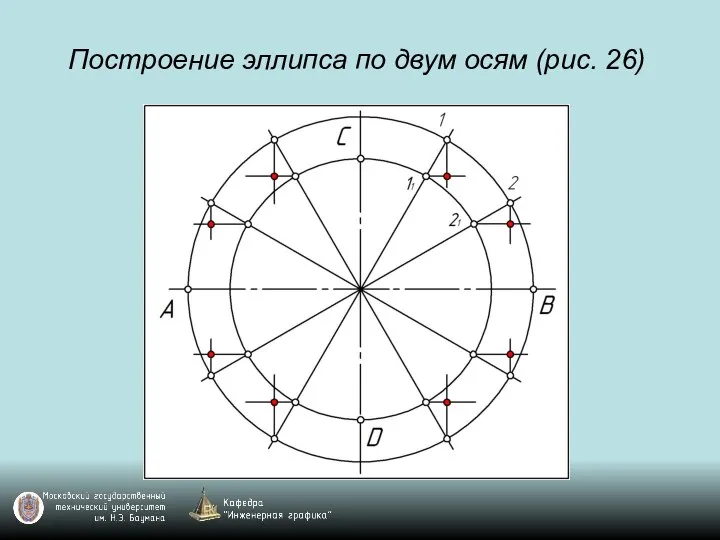
Слайд 28Построение эллипса по двум осям (рис. 26)
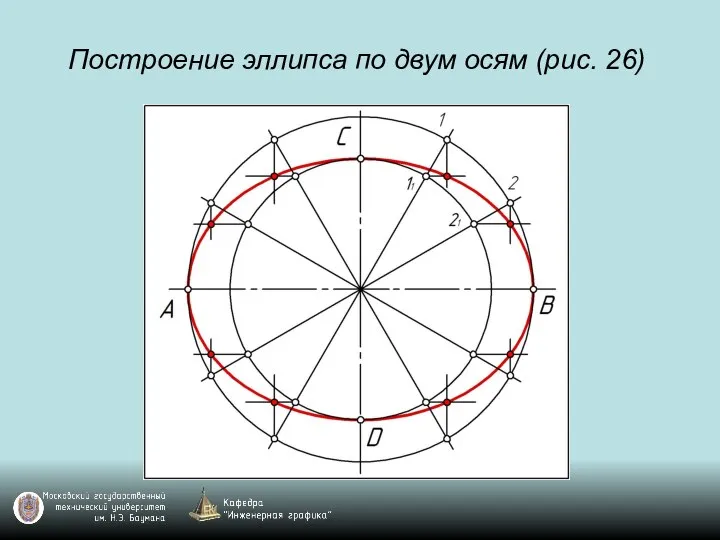
Слайд 29Пространственные кривые
Винтовая линия
Винтовая линия образуется при винтовом движении точки, т.е. при повороте
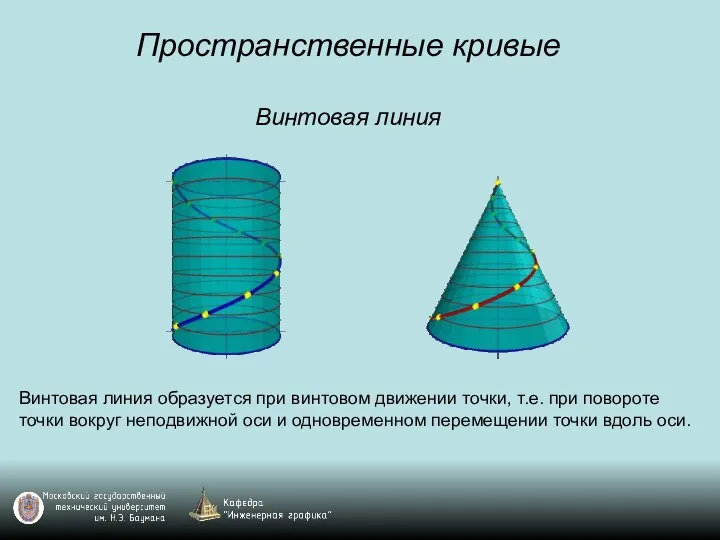
точки вокруг неподвижной оси и одновременном перемещении точки вдоль оси.
Слайд 30Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
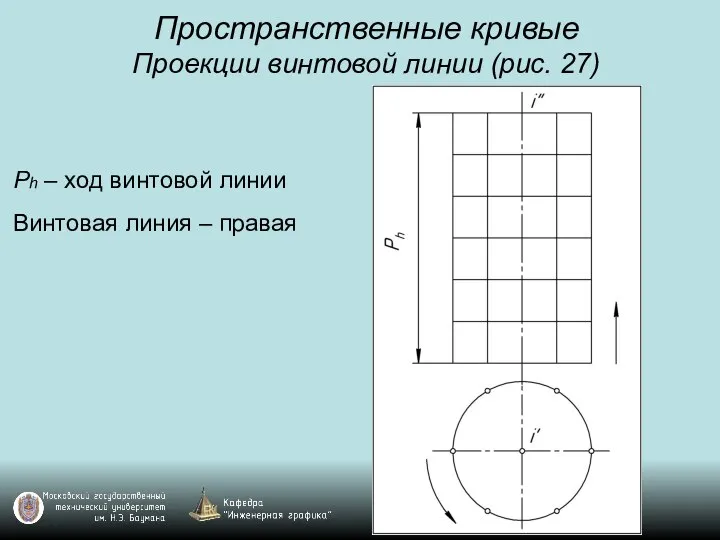
правая
Слайд 31Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
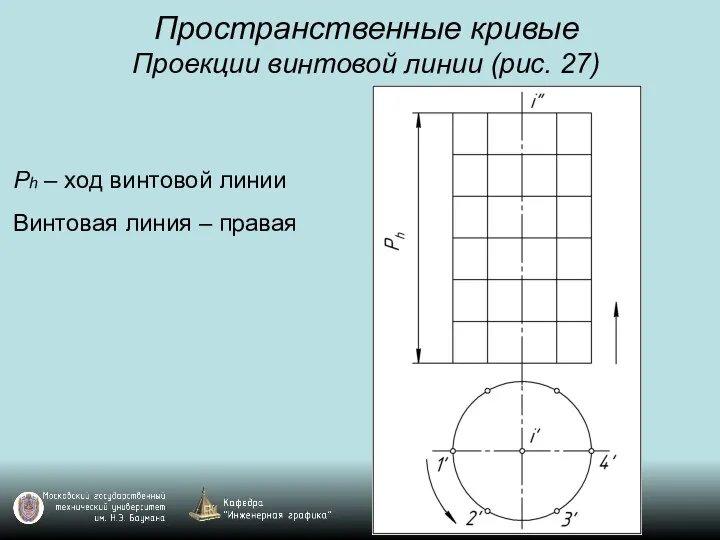
правая
Слайд 32Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
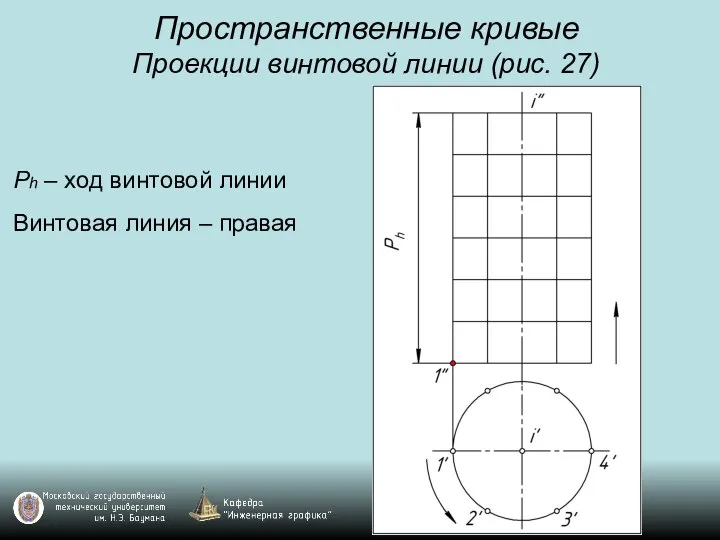
правая
Слайд 33Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
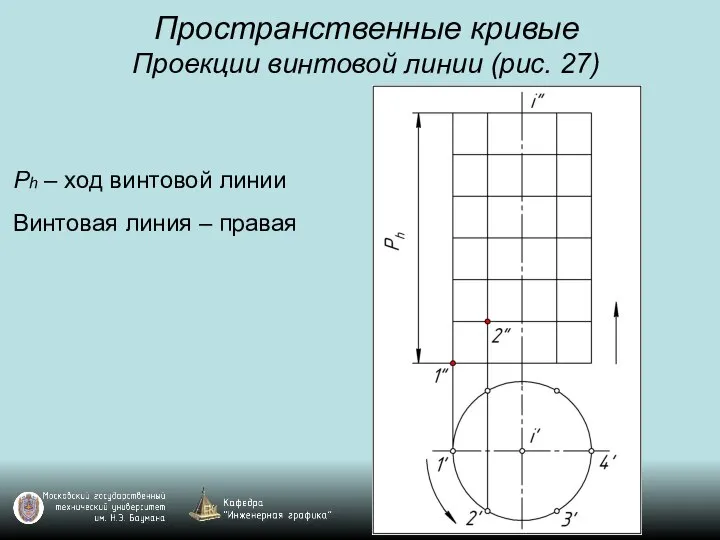
правая
Слайд 34Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
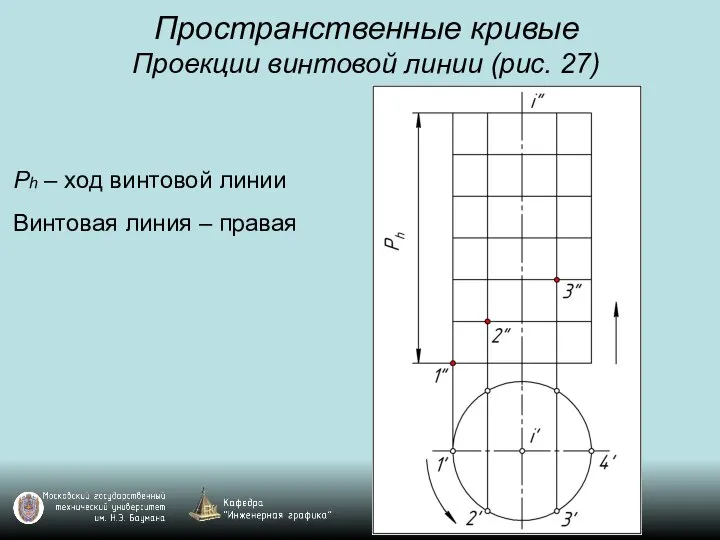
правая
Слайд 35Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
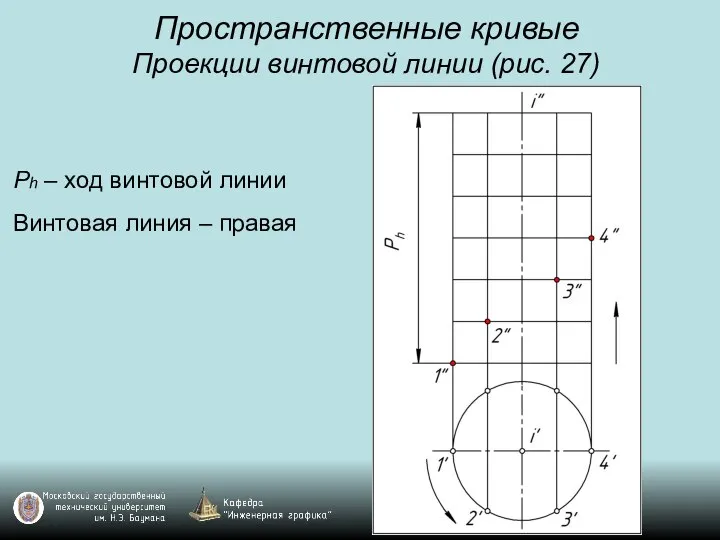
правая
Слайд 36Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
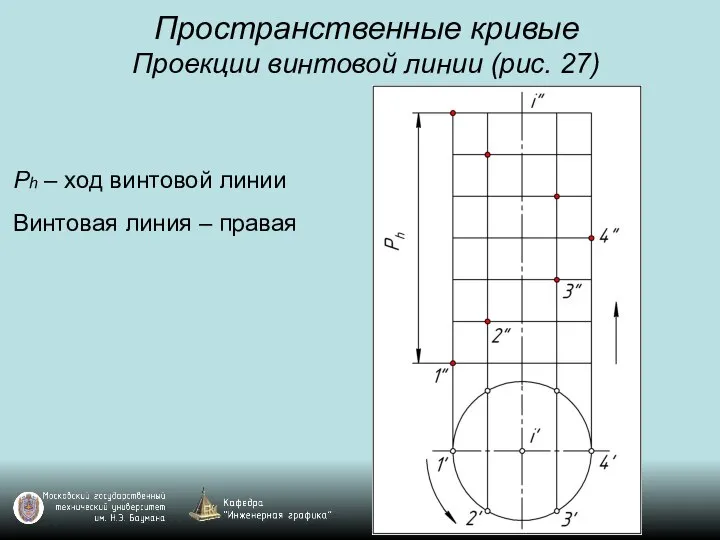
правая
Слайд 37Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –
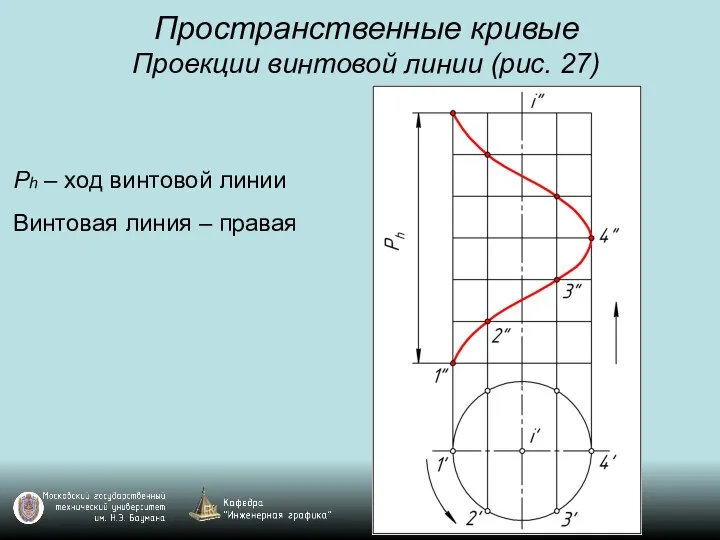
правая
Слайд 38Пространственные кривые
Проекции винтовой линии (рис. 27)
Ph – ход винтовой линии
Винтовая линия –

правая
Слайд 397. Образование и задание поверхностей
Задание поверхности с помощью каркаса (рис. 29)
Задание поверхности
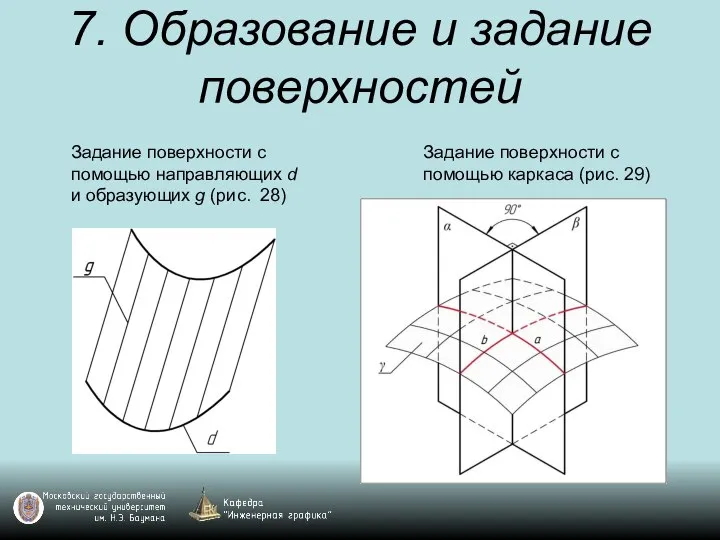
с помощью направляющих d и образующих g (рис. 28)
Слайд 40Очерк поверхности
Для большей наглядности в ряде случаев используют очерк поверхности (рис. 30).

Слайд 41Общее правило построения проекции точки, принадлежащей поверхности:
Для построения проекции точки, принадлежащей поверхности,

надо воспользоваться проекциями линии, принадлежащей поверхности и проходящей через заданную точку.
Слайд 42Обзор поверхностей
Можно группировать поверхности:
по форме образующей: линейчатые, нелинейчатые;
по движению образующей: параллельный перенос,

вращение, винтовое;
по возможности развернуть на плоскость: развертываемые, неразвертываемые.
Слайд 43Одна и та же поверхность может быть образована разными образующими с разными
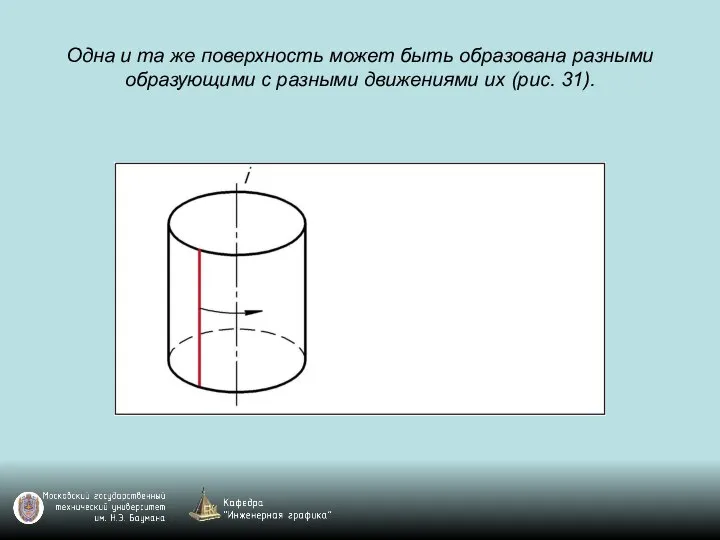
движениями их (рис. 31).
Слайд 44Одна и та же поверхность может быть образована разными образующими с разными
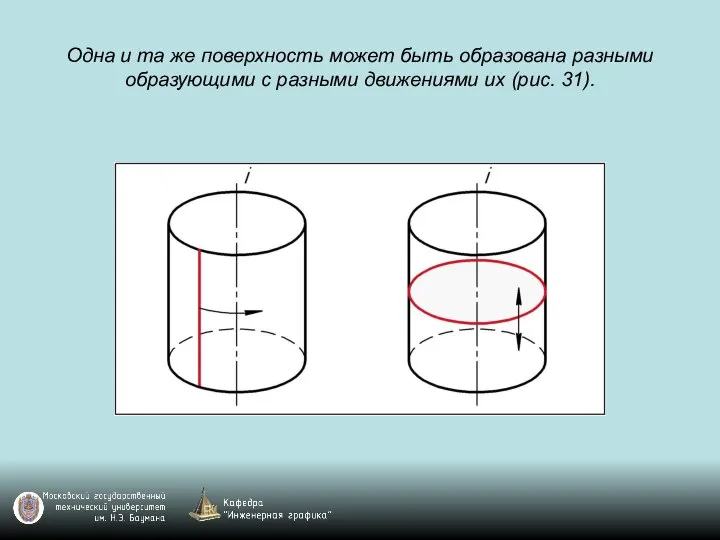
движениями их (рис. 31).
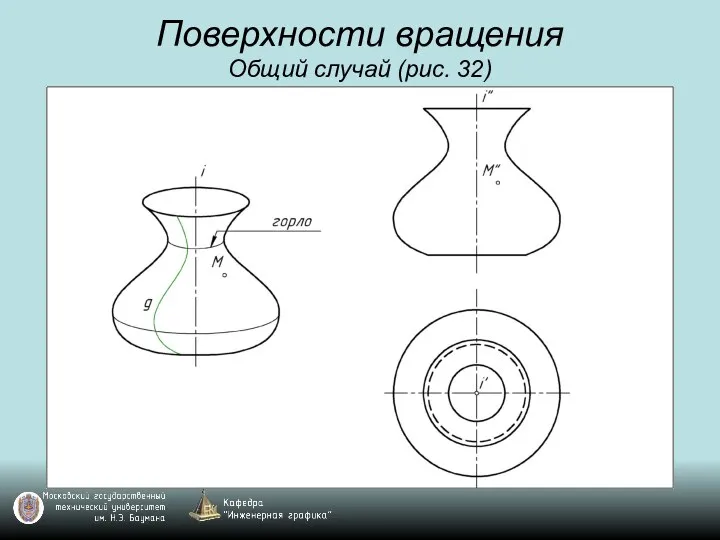
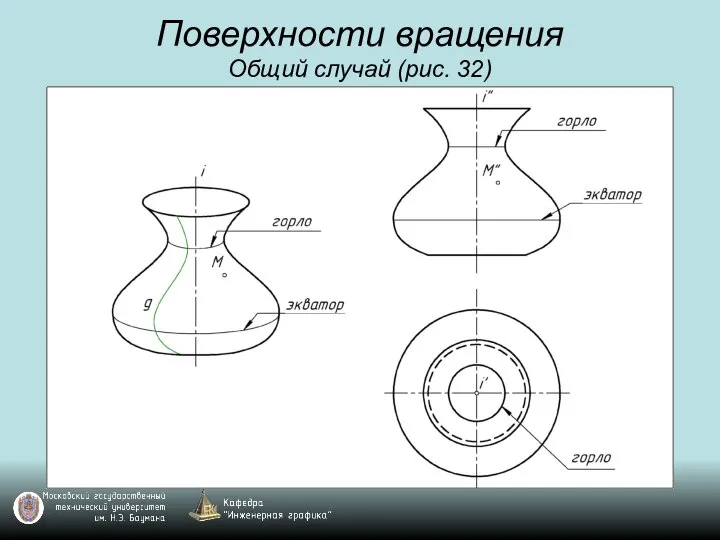
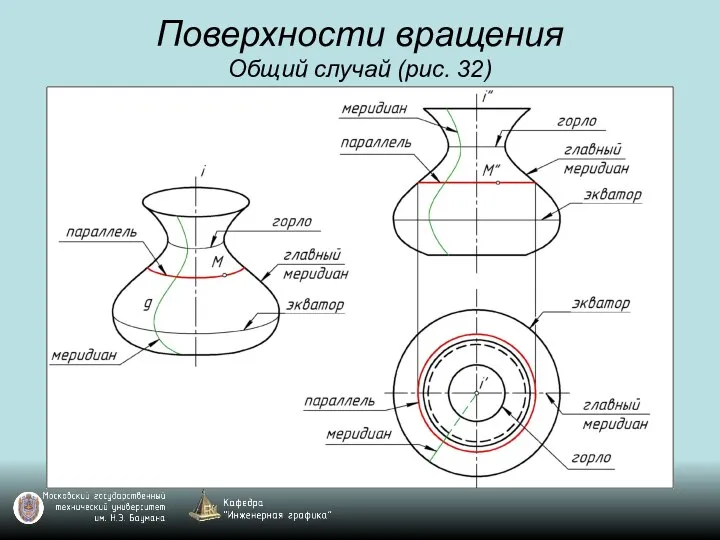
Слайд 45Поверхности вращения
Общий случай (рис. 32)

Слайд 46Поверхности вращения
Общий случай (рис. 32)
Слайд 47Поверхности вращения
Общий случай (рис. 32)
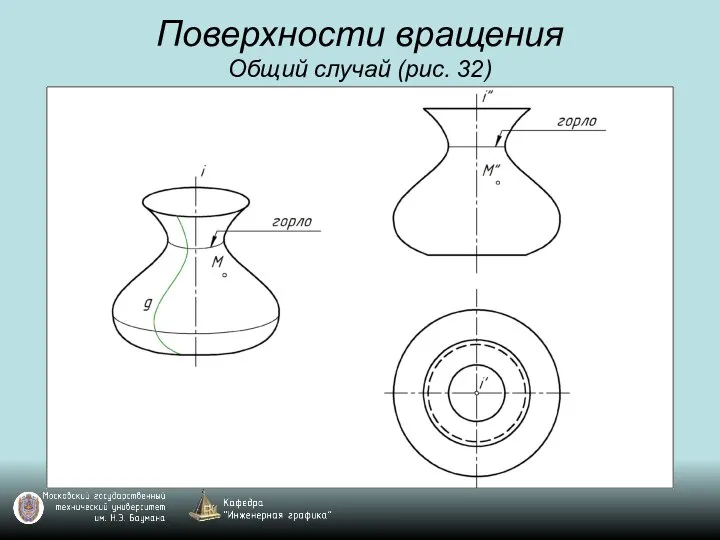
Слайд 48Поверхности вращения
Общий случай (рис. 32)
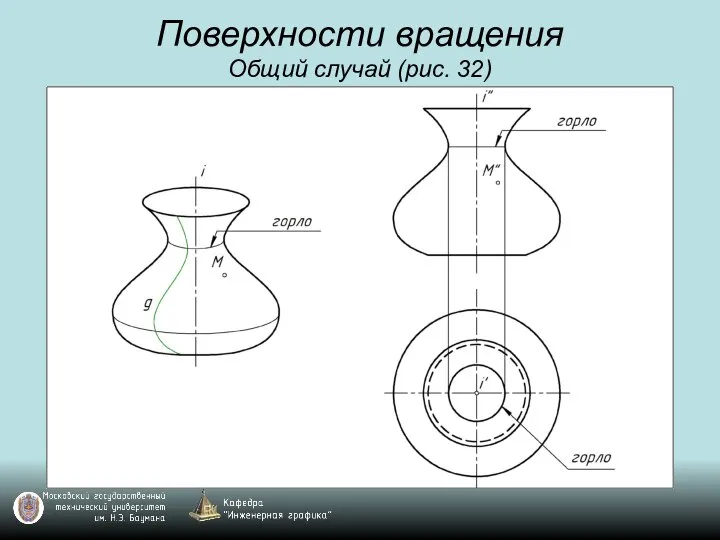
Слайд 49Поверхности вращения
Общий случай (рис. 32)
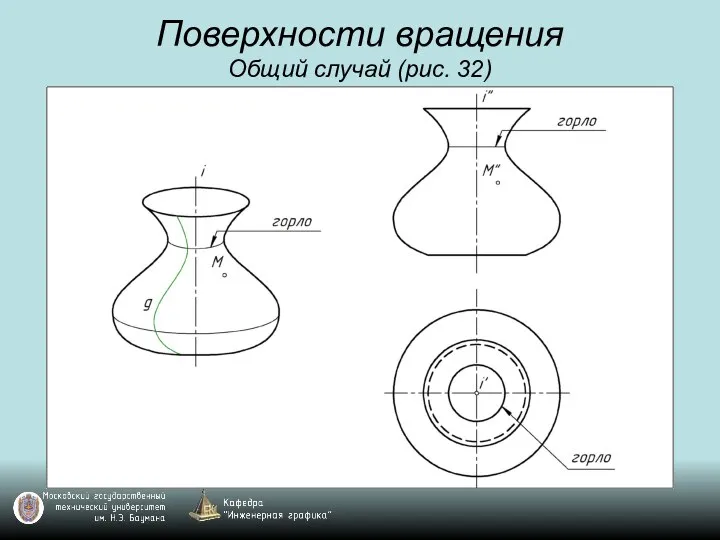
Слайд 50Поверхности вращения
Общий случай (рис. 32)
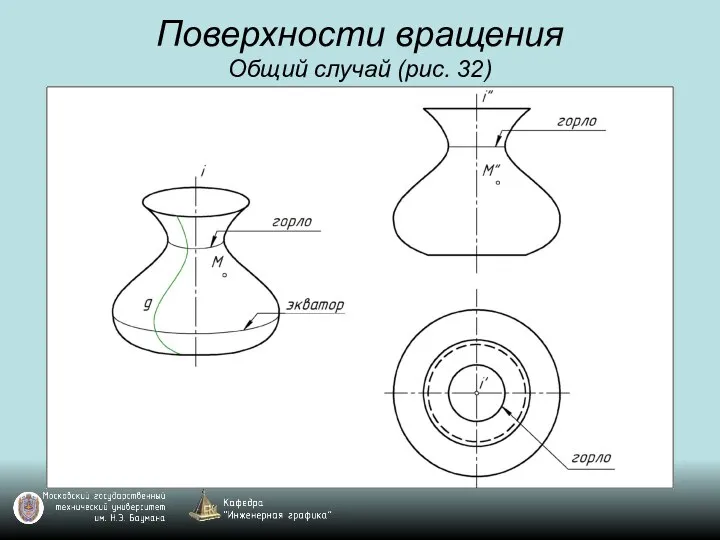
Слайд 51Поверхности вращения
Общий случай (рис. 32)
Слайд 52Поверхности вращения
Общий случай (рис. 32)
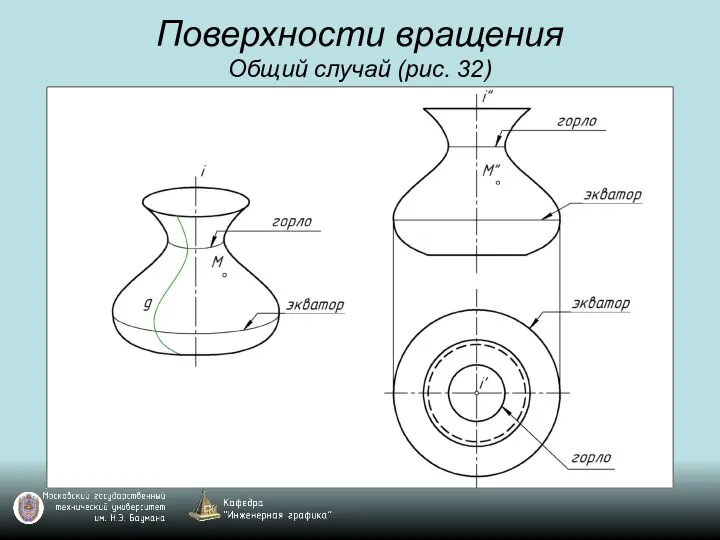
Слайд 53Поверхности вращения
Общий случай (рис. 32)
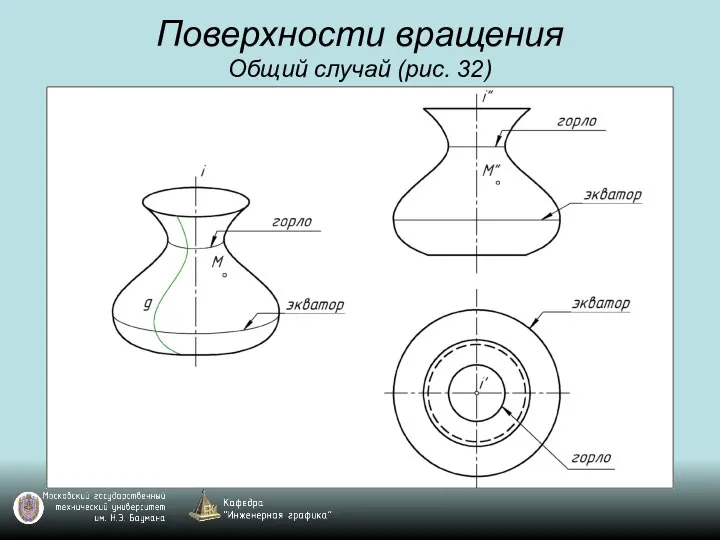
Слайд 54Поверхности вращения
Общий случай (рис. 32)
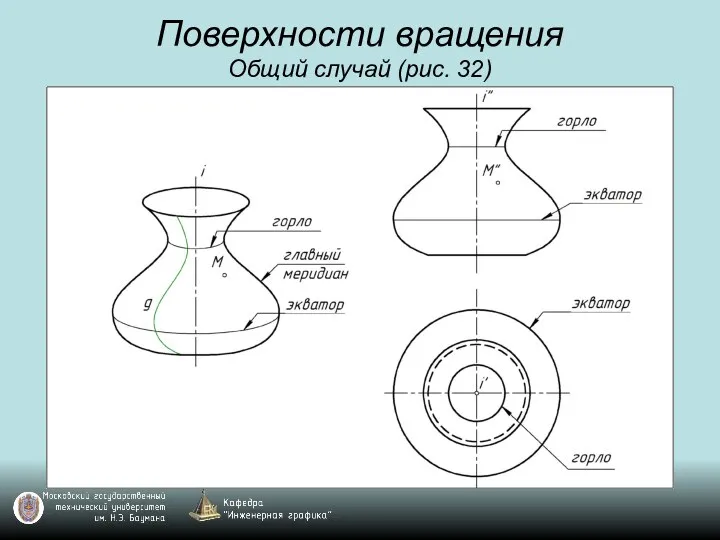
Слайд 55Поверхности вращения
Общий случай (рис. 32)
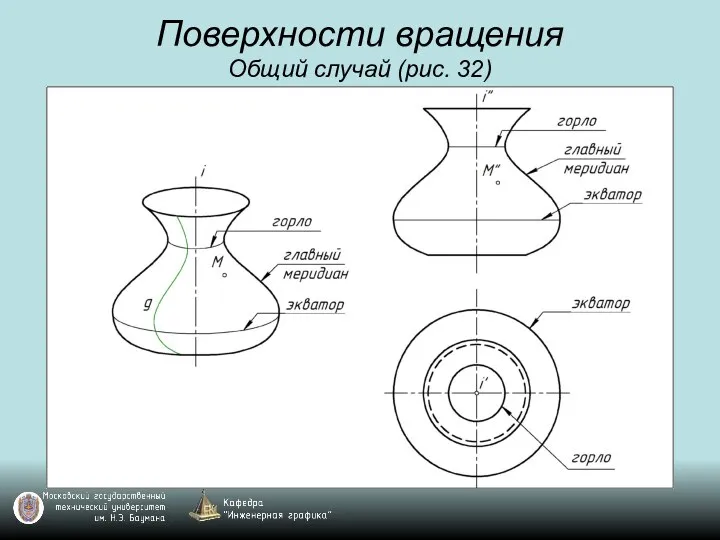
Слайд 56Поверхности вращения
Общий случай (рис. 32)
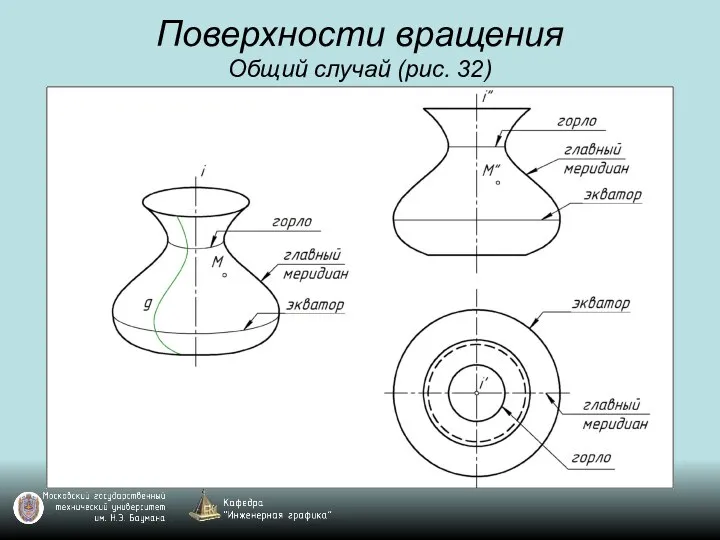
Слайд 57Поверхности вращения
Общий случай (рис. 32)
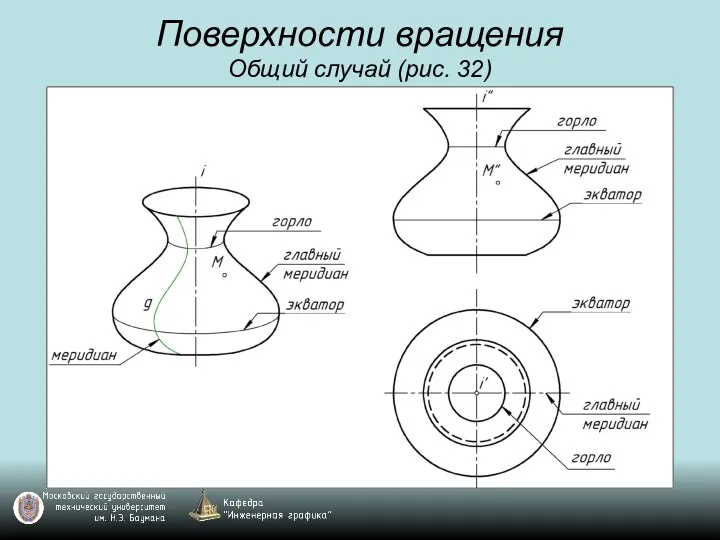
Слайд 58Поверхности вращения
Общий случай (рис. 32)
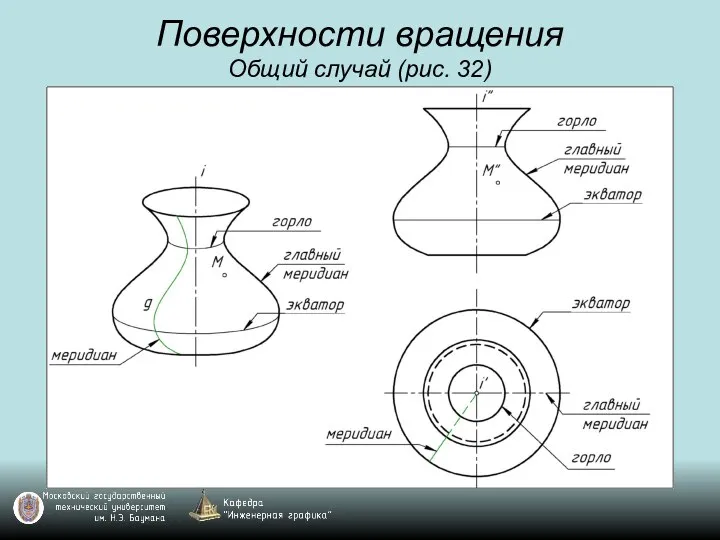
Слайд 59Поверхности вращения
Общий случай (рис. 32)
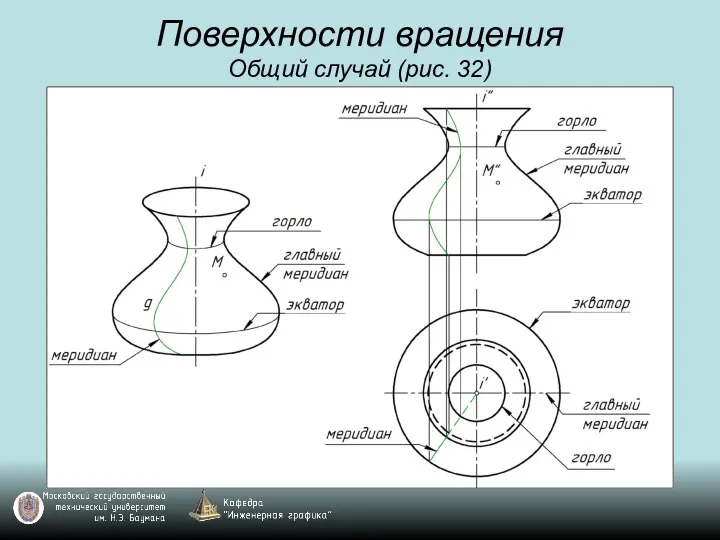
Слайд 60Поверхности вращения
Общий случай (рис. 32)
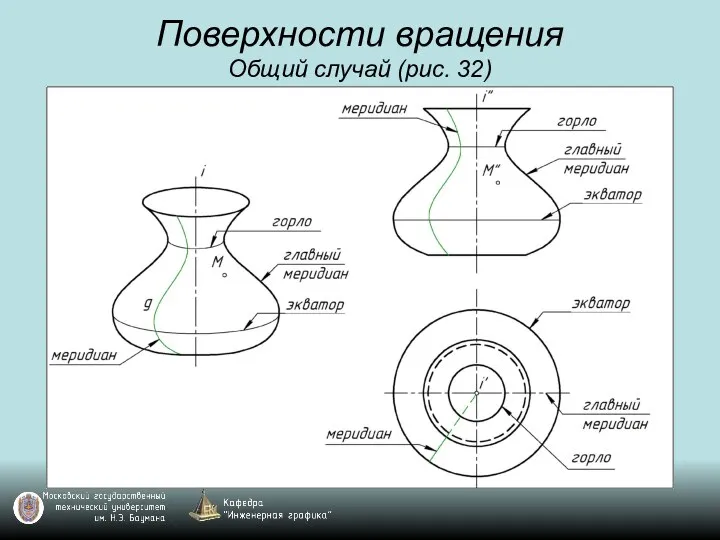
Слайд 61Поверхности вращения
Общий случай (рис. 32)
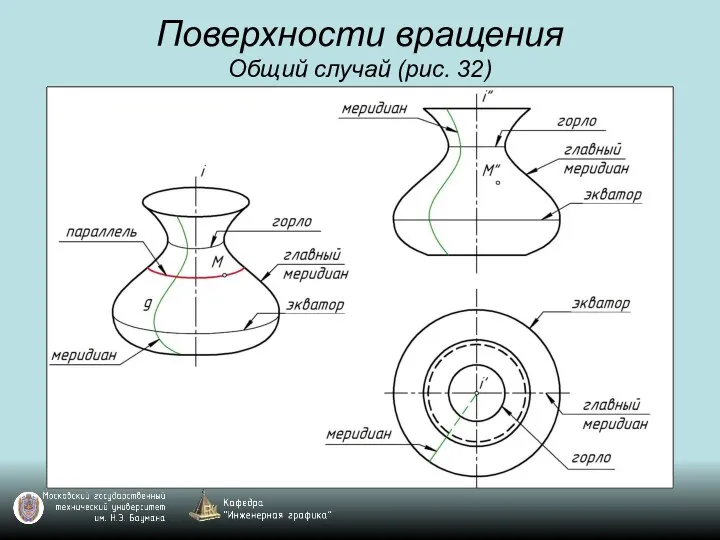
Слайд 62Поверхности вращения
Общий случай (рис. 32)
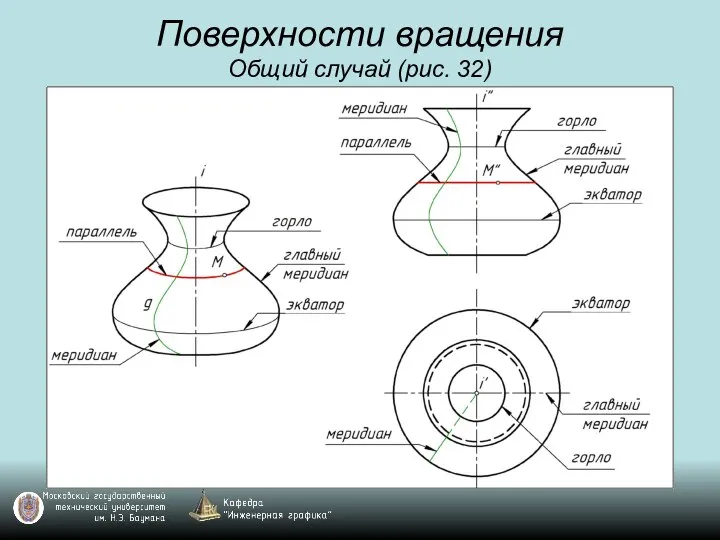
Слайд 63Поверхности вращения
Общий случай (рис. 32)
Слайд 64Поверхности вращения
Общий случай (рис. 32)
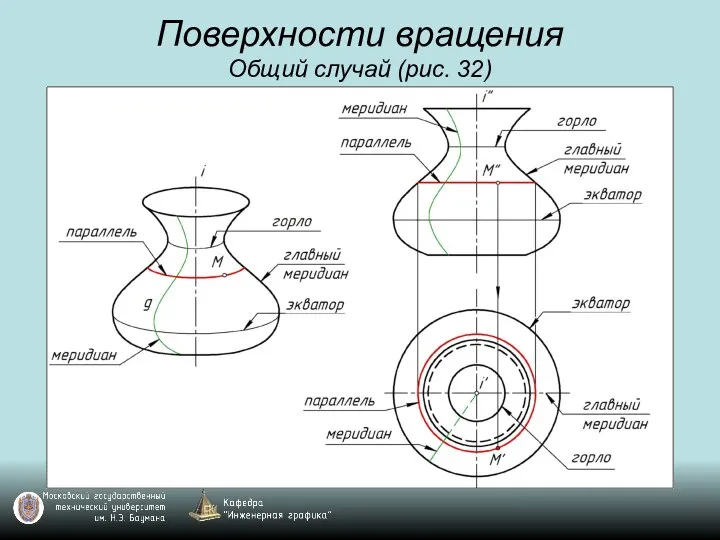
Слайд 65Поверхности вращения с образующей g – прямой линией.
Укажите положение образующей g относительно

оси i (рис. 33).
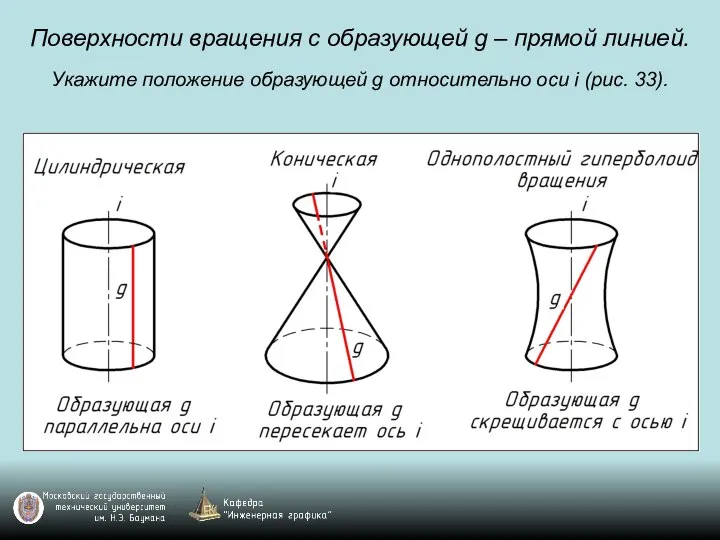
Слайд 66Поверхности вращения с образующей g – прямой линией.
Укажите положение образующей g относительно

оси i (рис. 33).
Слайд 67Поверхности вращения с образующей g – прямой линией.
Укажите положение образующей g относительно

оси i (рис. 33).
Слайд 68Поверхности вращения с образующей g – прямой линией.
Укажите положение образующей g относительно
оси i (рис. 33).
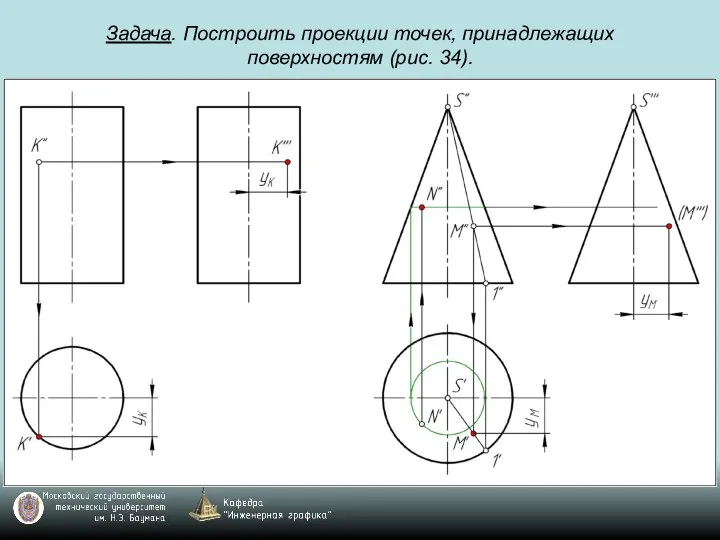
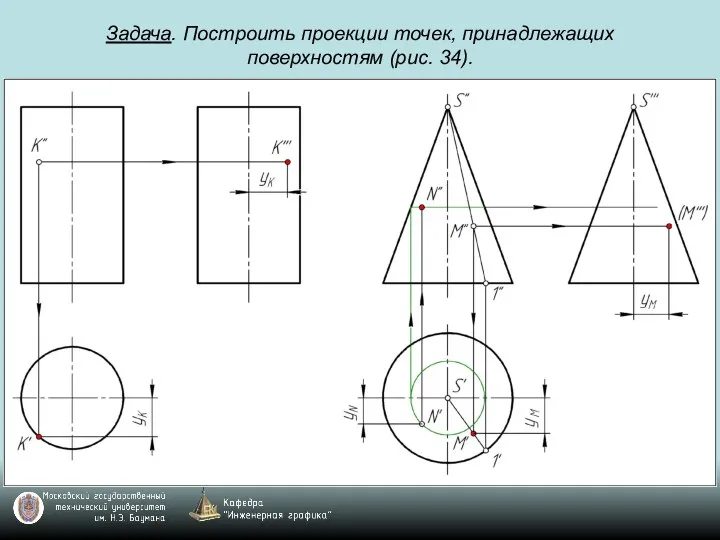
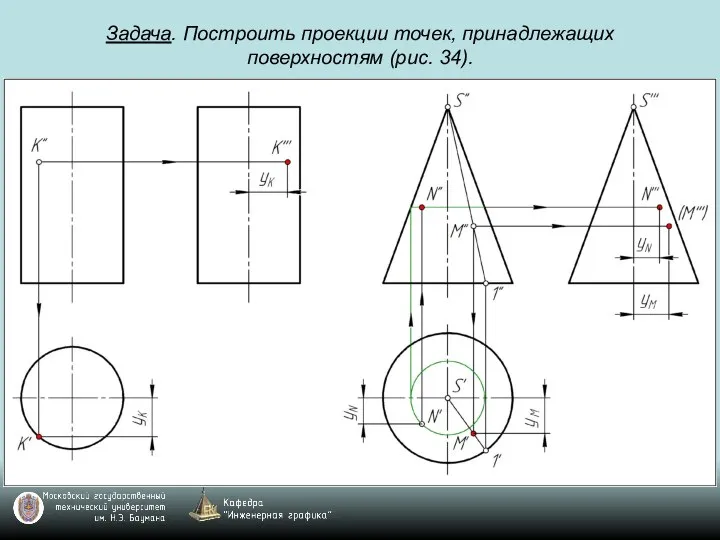
Слайд 69Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
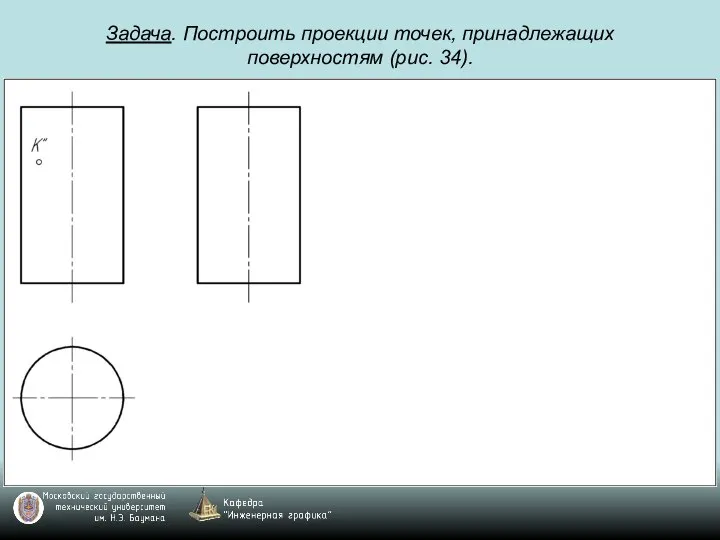
Слайд 70Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
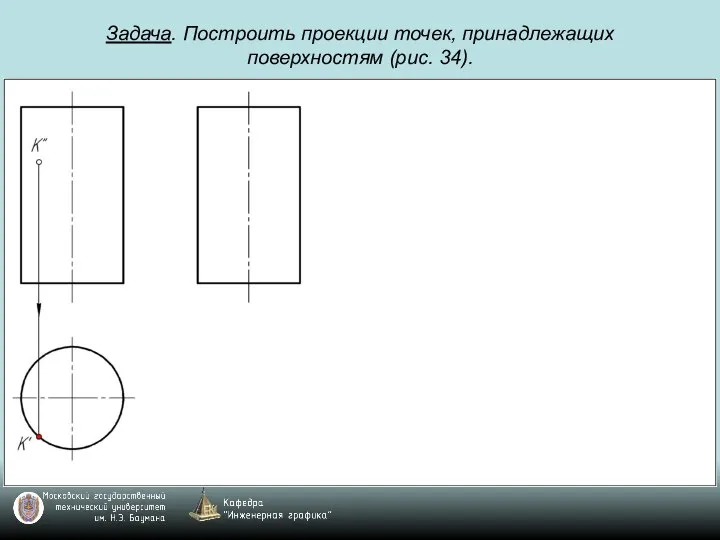
Слайд 71Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
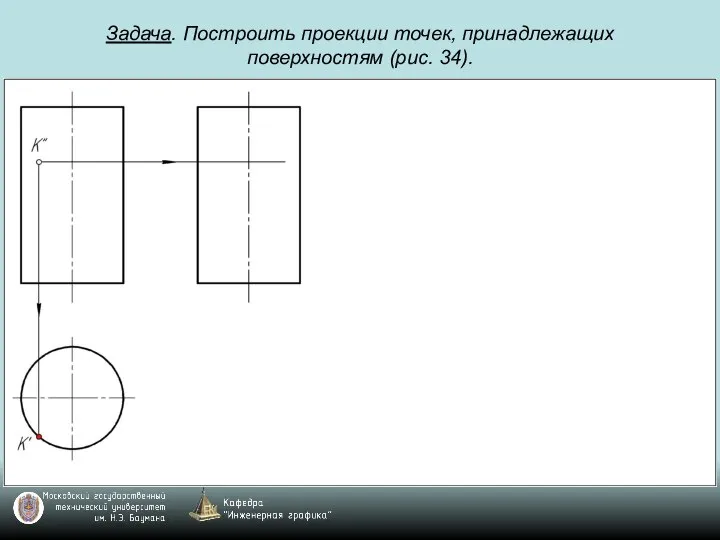
Слайд 72Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
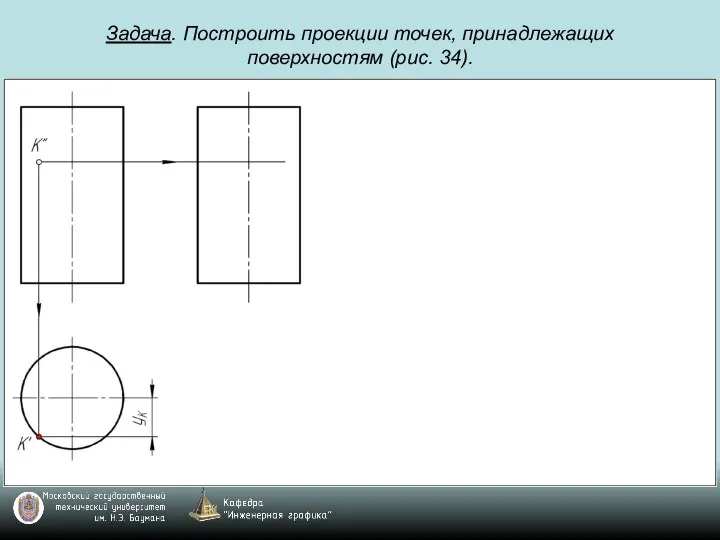
Слайд 73Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
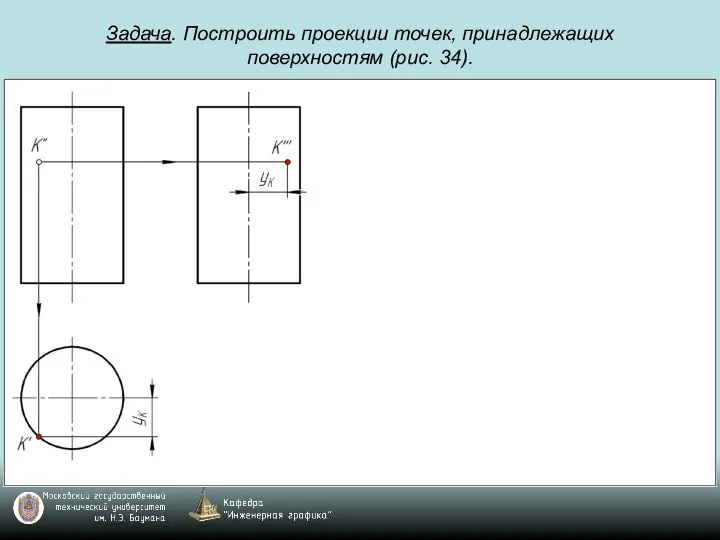
Слайд 74Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
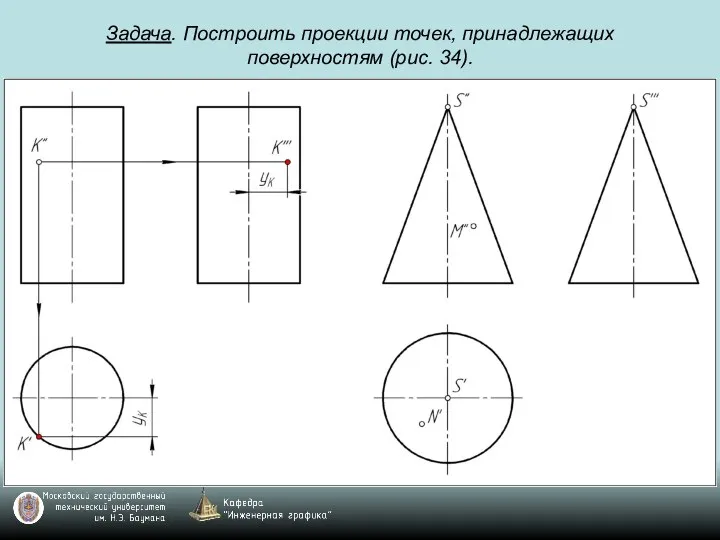
Слайд 75Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
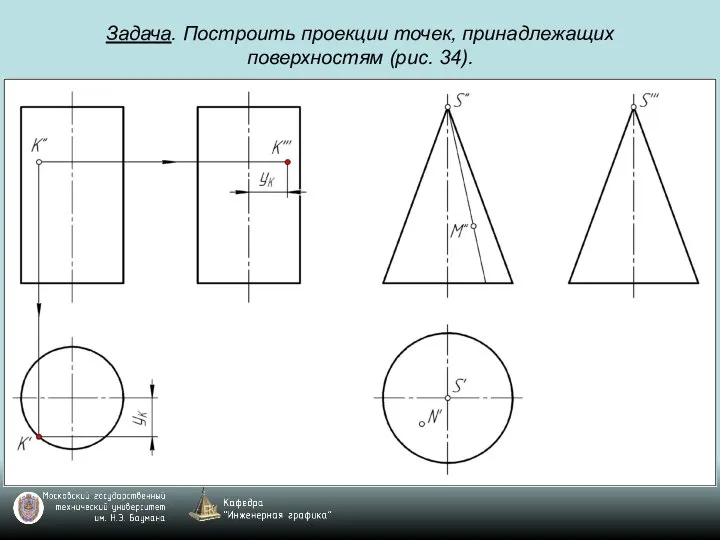
Слайд 76Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
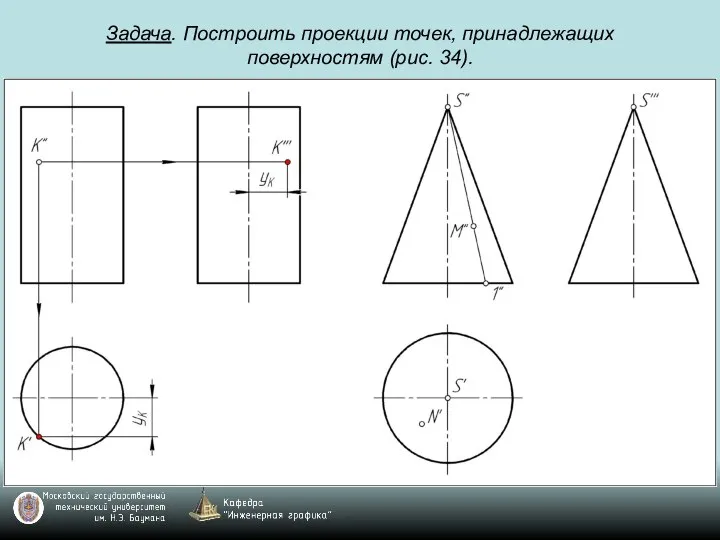
Слайд 77Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
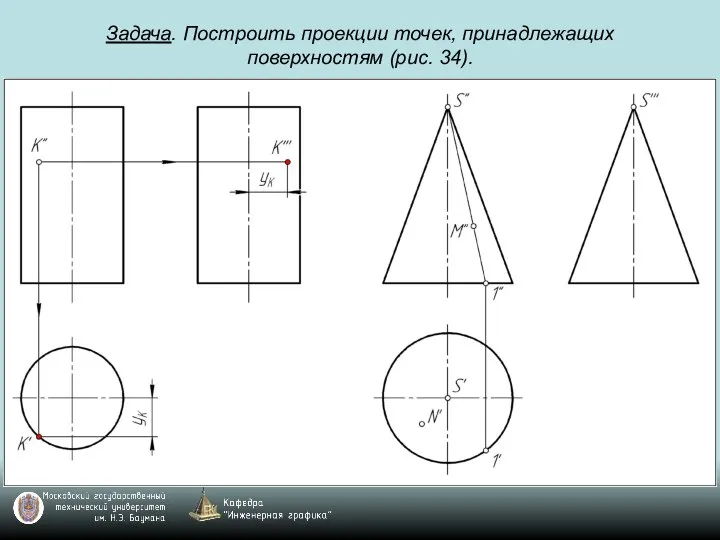
Слайд 78Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
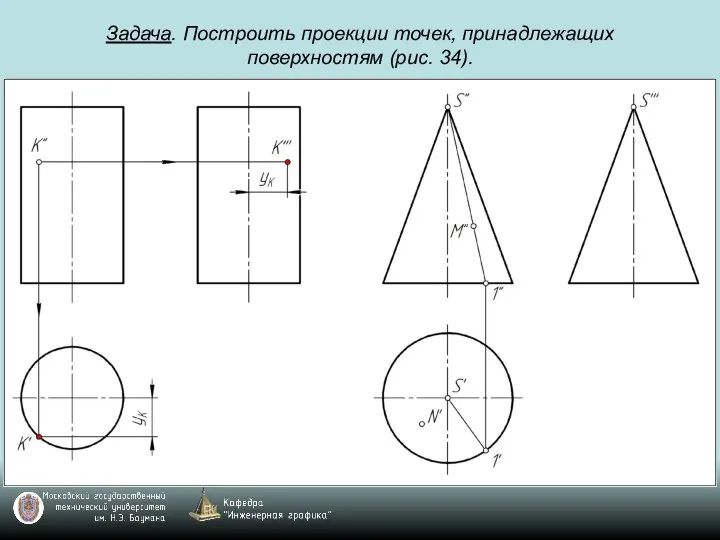
Слайд 79Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
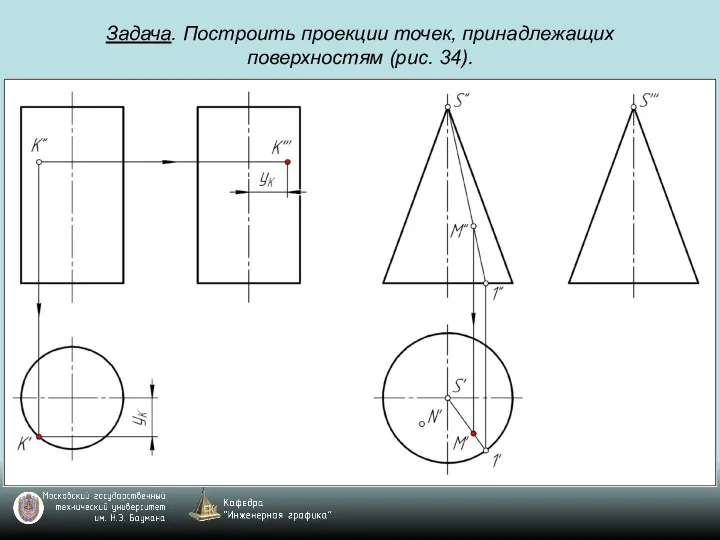
Слайд 80Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
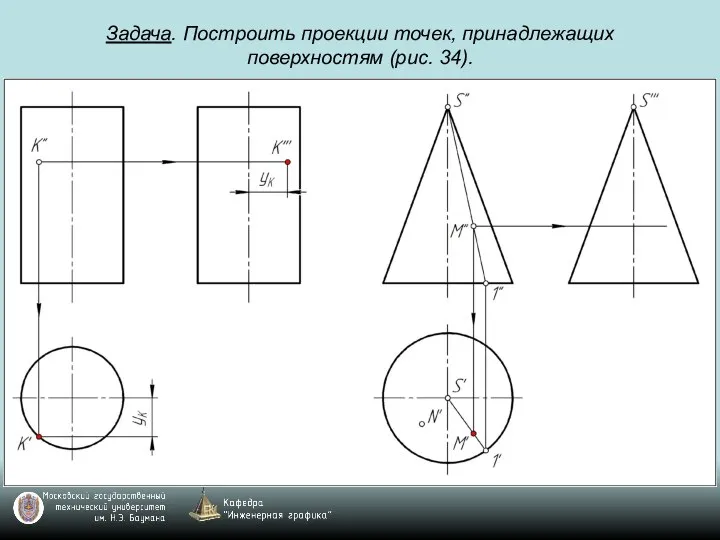
Слайд 81Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
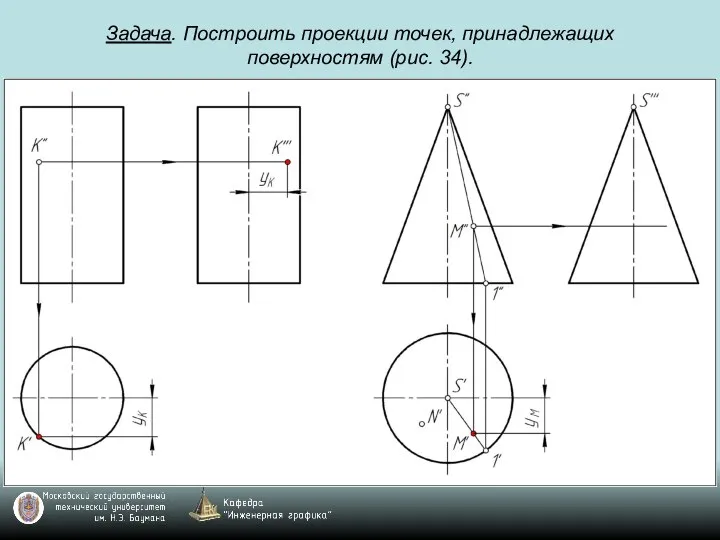
Слайд 82Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
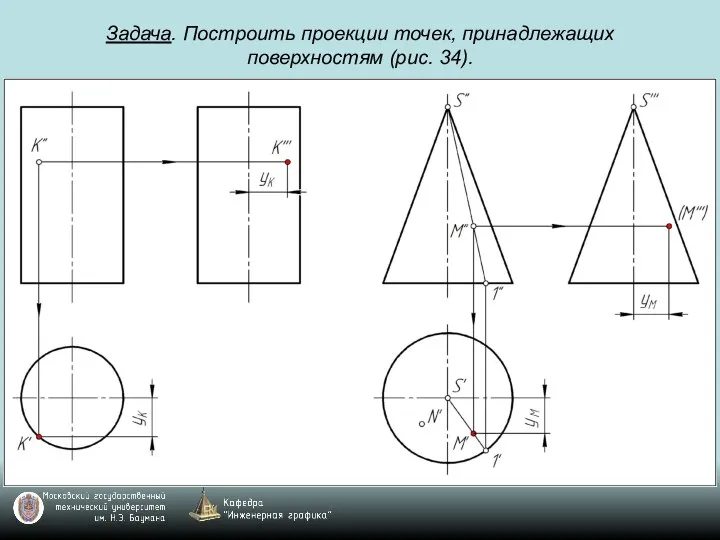
Слайд 83Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
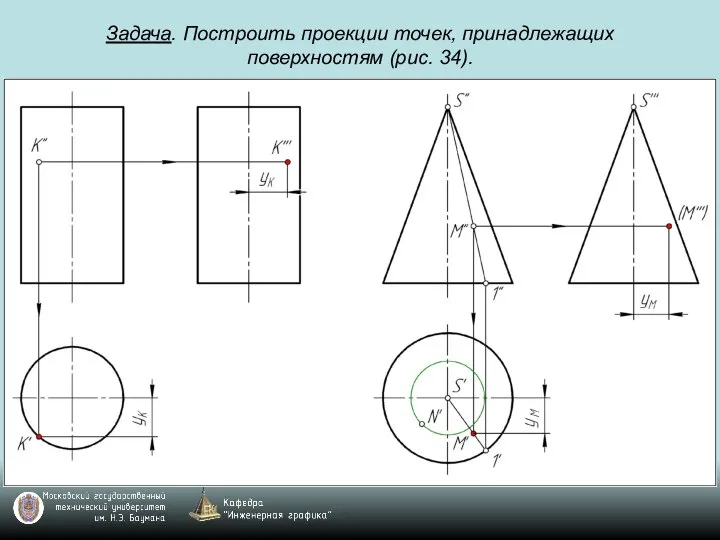
Слайд 84Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
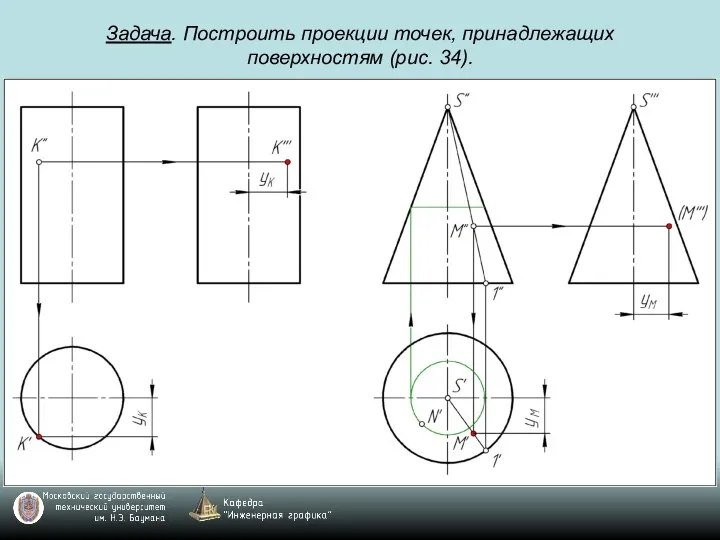
Слайд 85Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
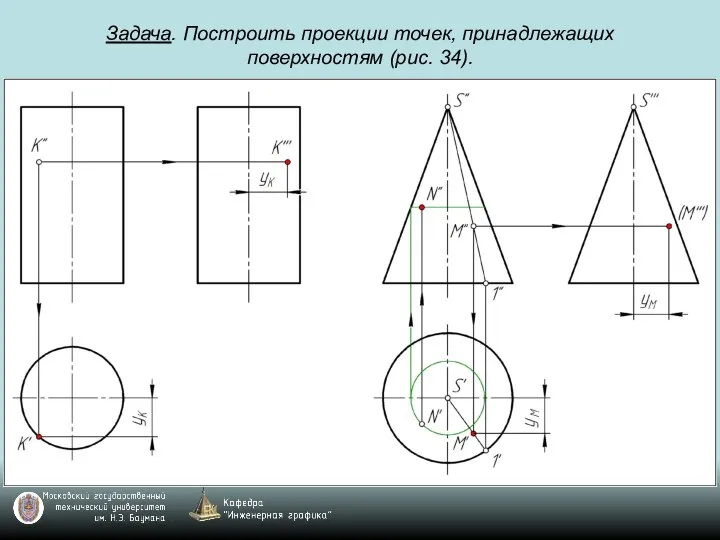
Слайд 86Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
Слайд 87Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
Слайд 88Задача. Построить проекции точек, принадлежащих поверхностям (рис. 34).
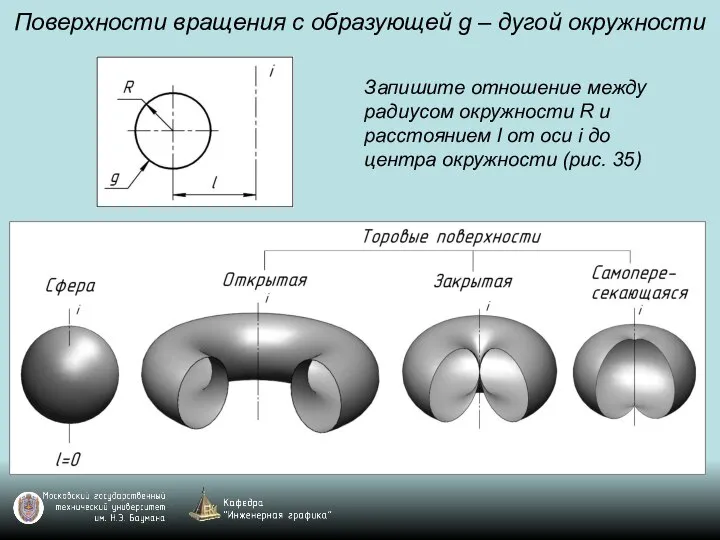
Слайд 89Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом окружности
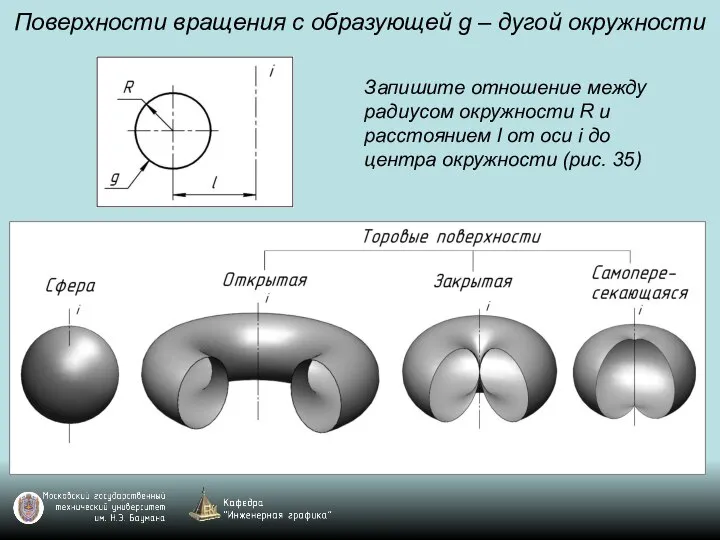
R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 90Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом окружности
R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 91Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом окружности
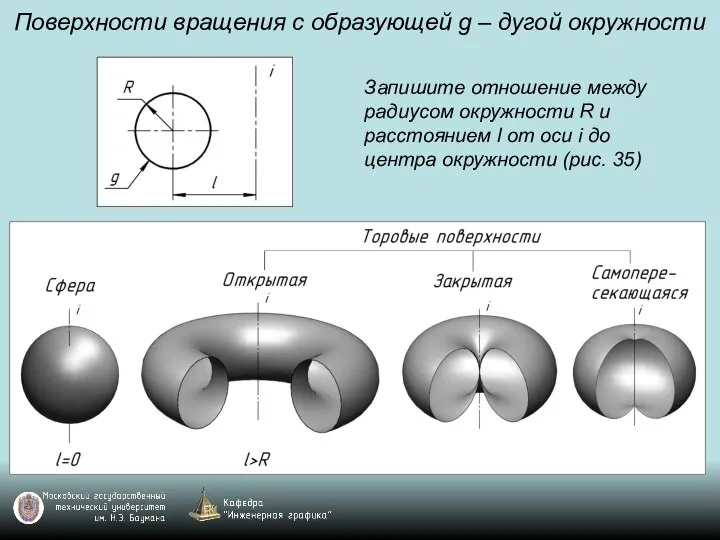
R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 92Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом окружности
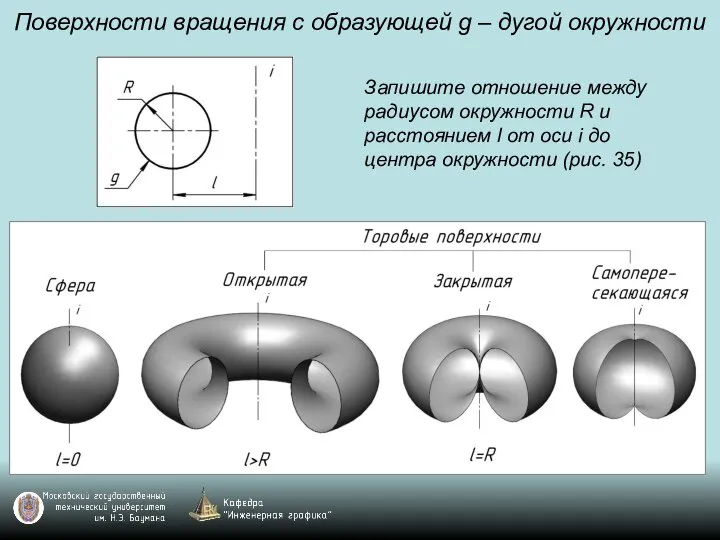
R и расстоянием l от оси i до центра окружности (рис. 35)
Слайд 93Поверхности вращения с образующей g – дугой окружности
Запишите отношение между радиусом окружности
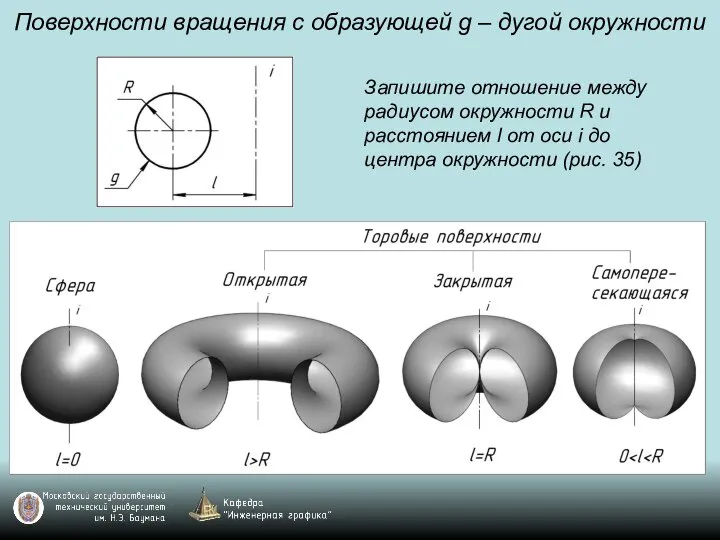
R и расстоянием l от оси i до центра окружности (рис. 35)
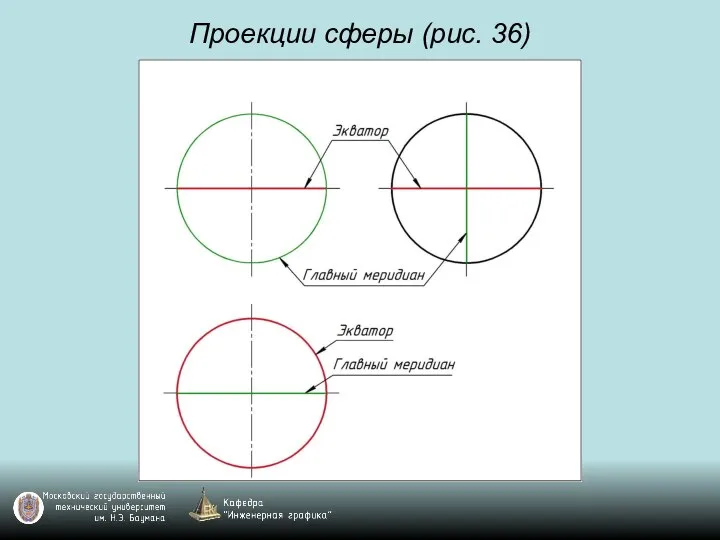
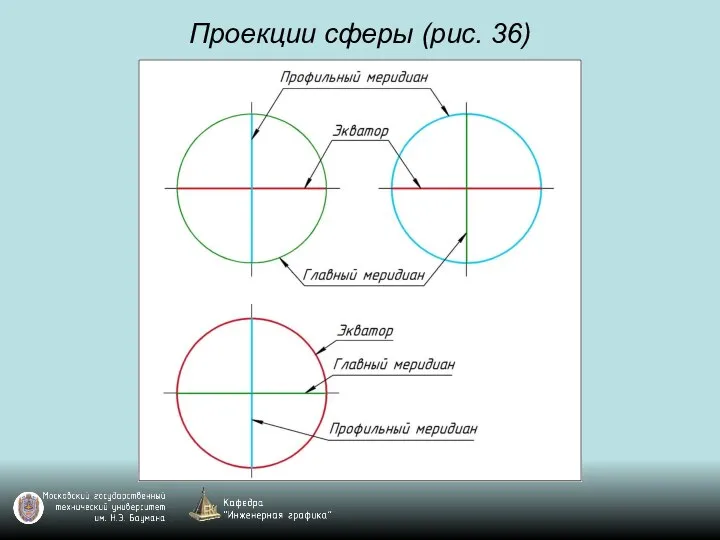
Слайд 98Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
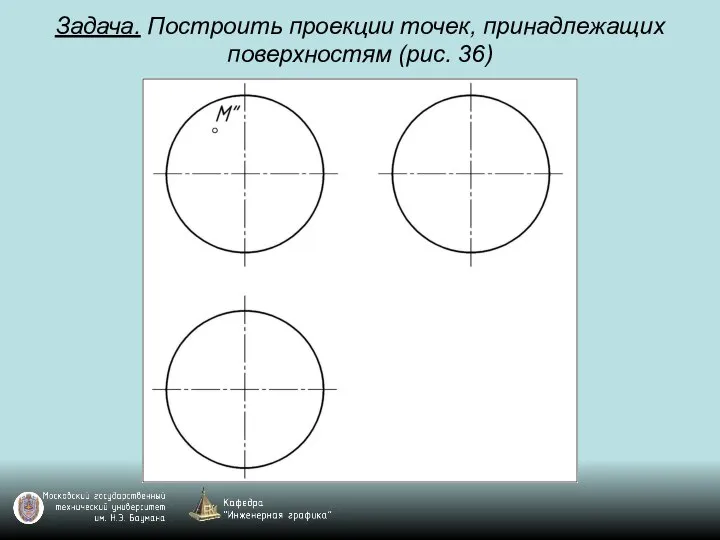
Слайд 99Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
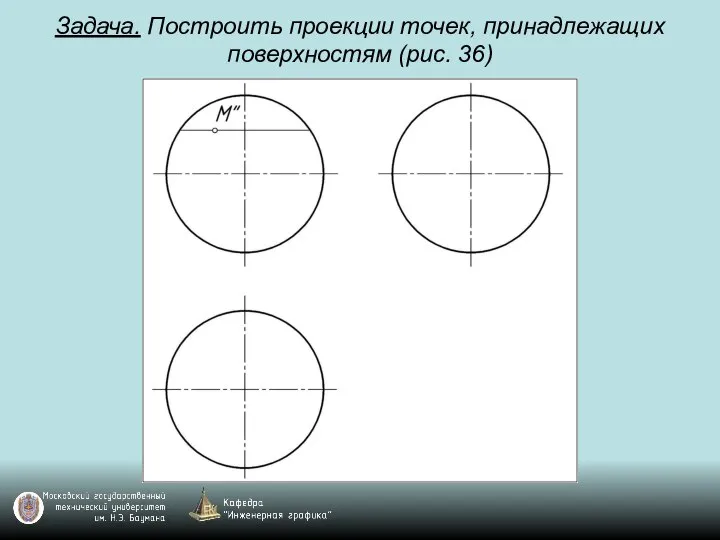
Слайд 100Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
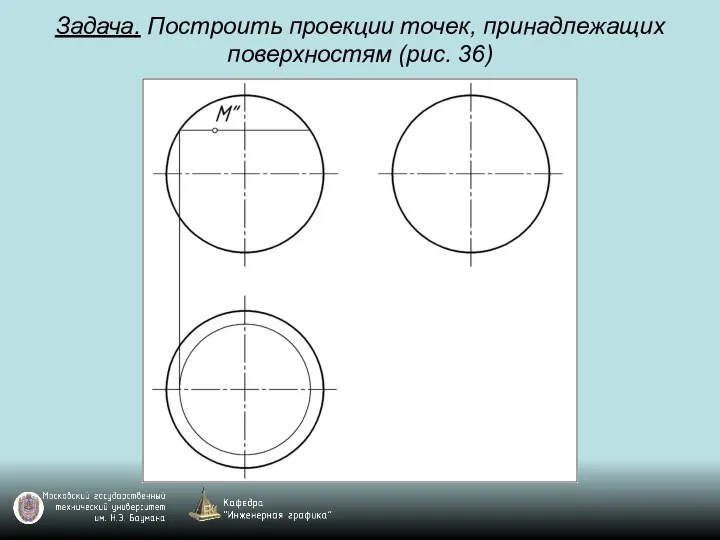
Слайд 101Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
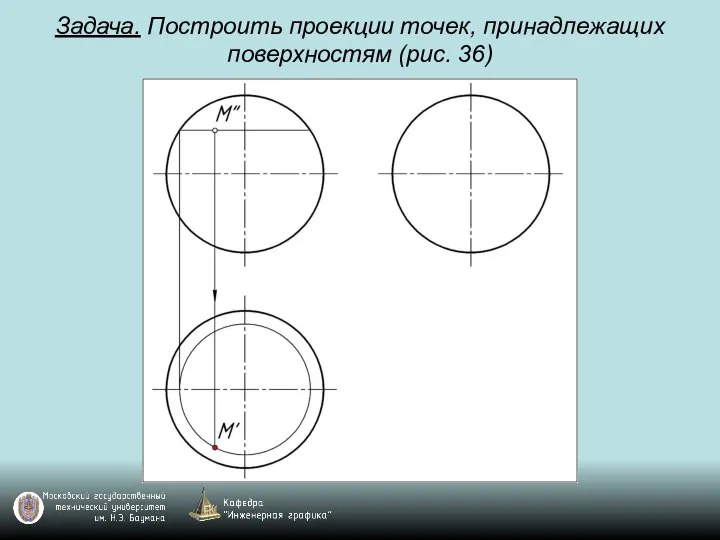
Слайд 102Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
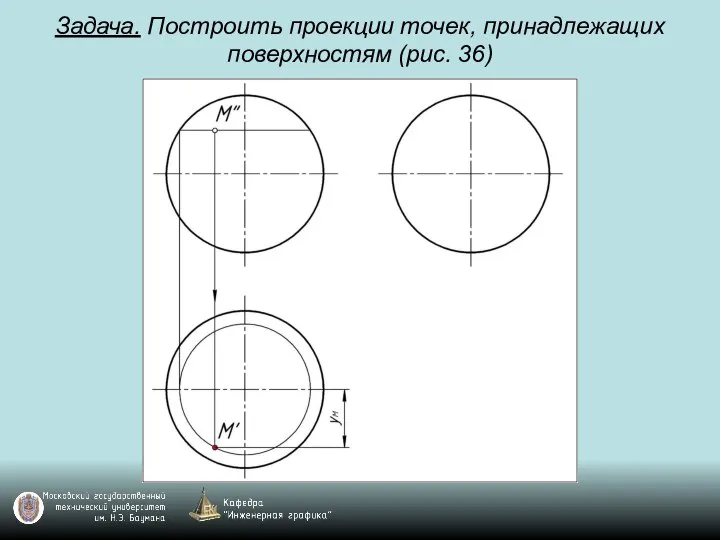
Слайд 103Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
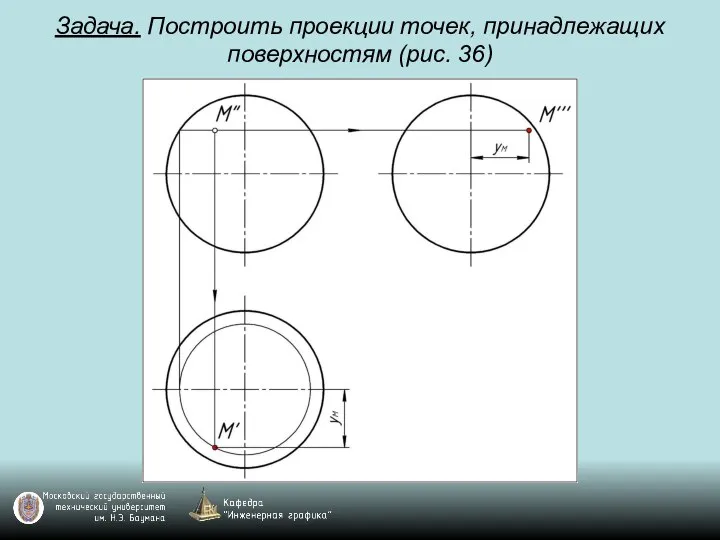
Слайд 104Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
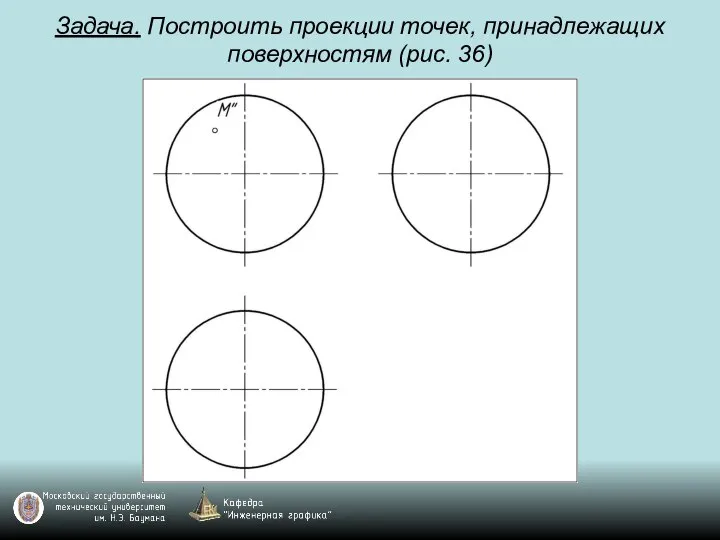
Слайд 105Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
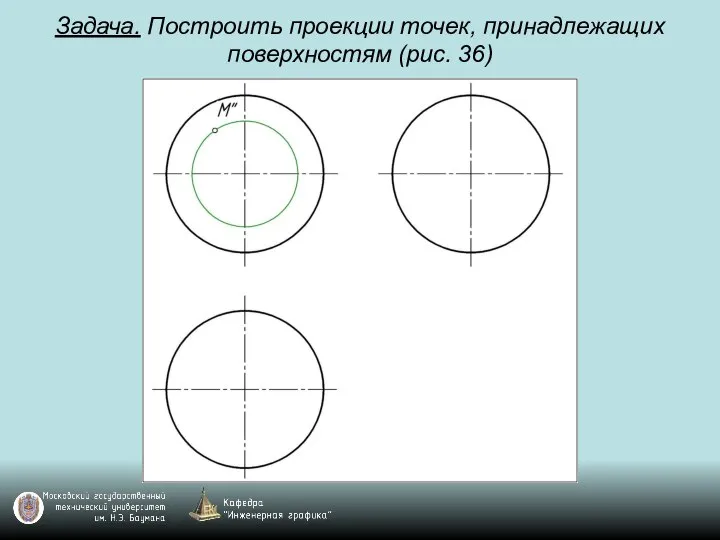
Слайд 106Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
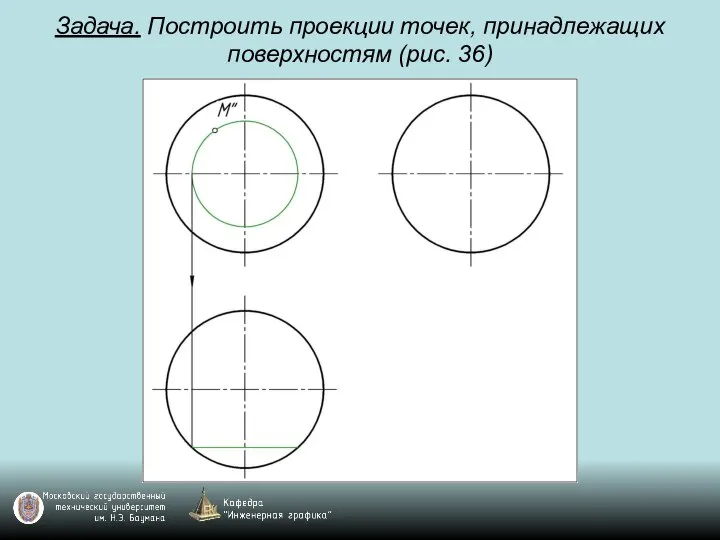
Слайд 107Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
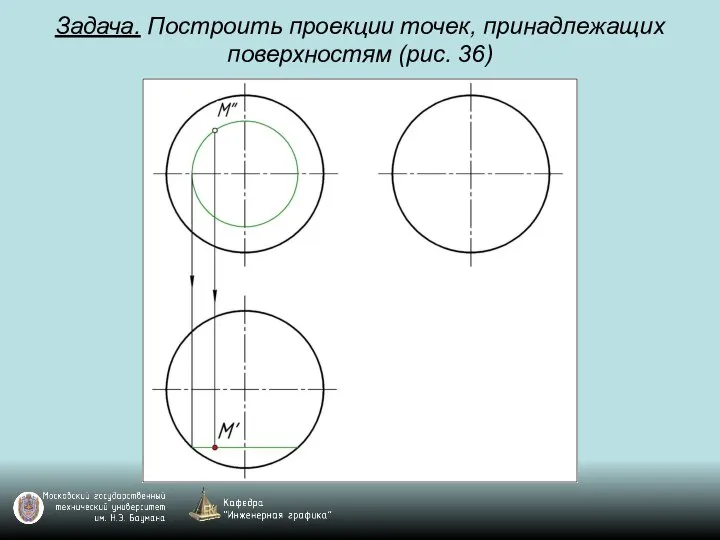
Слайд 108Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
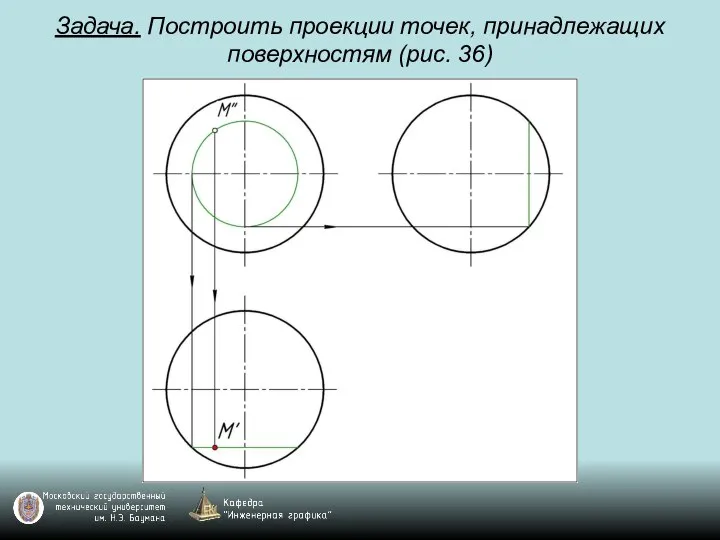
Слайд 109Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
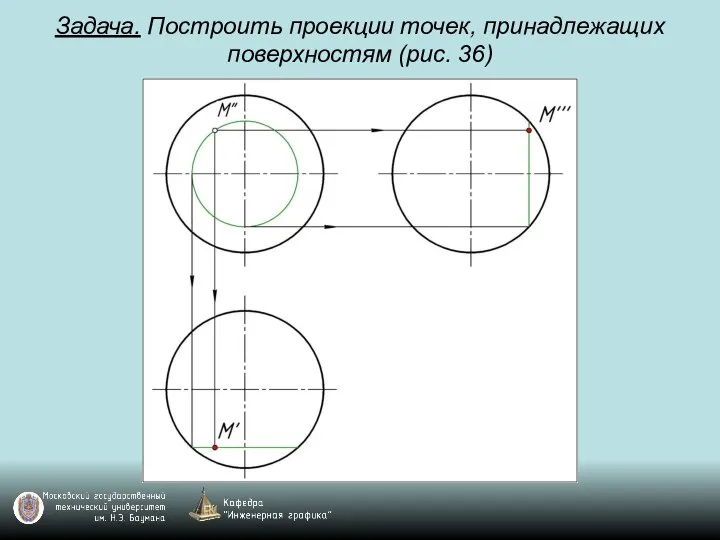
Слайд 110Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

Слайд 111Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

Слайд 112Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
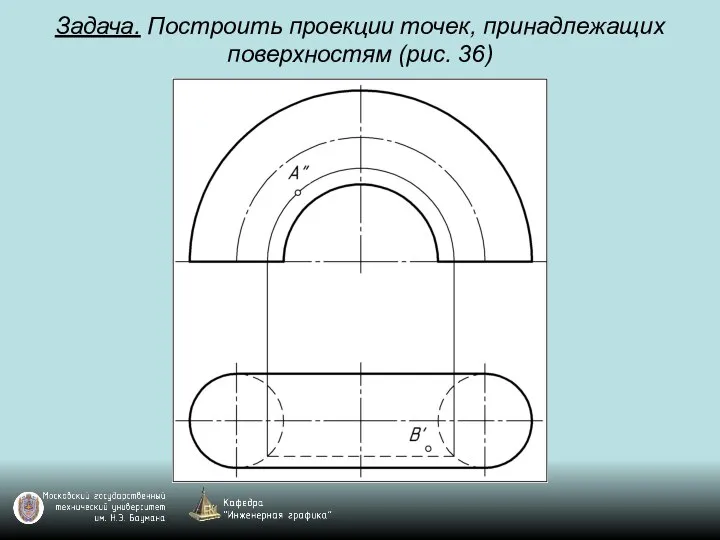
Слайд 113Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
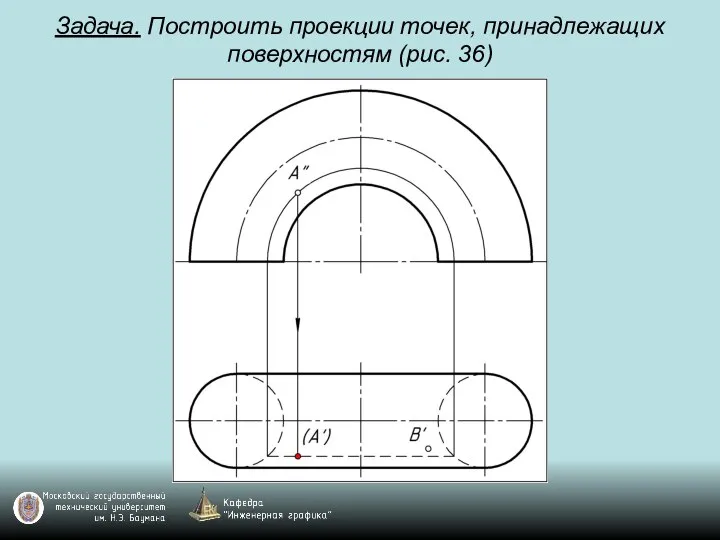
Слайд 114Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)

Слайд 115Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
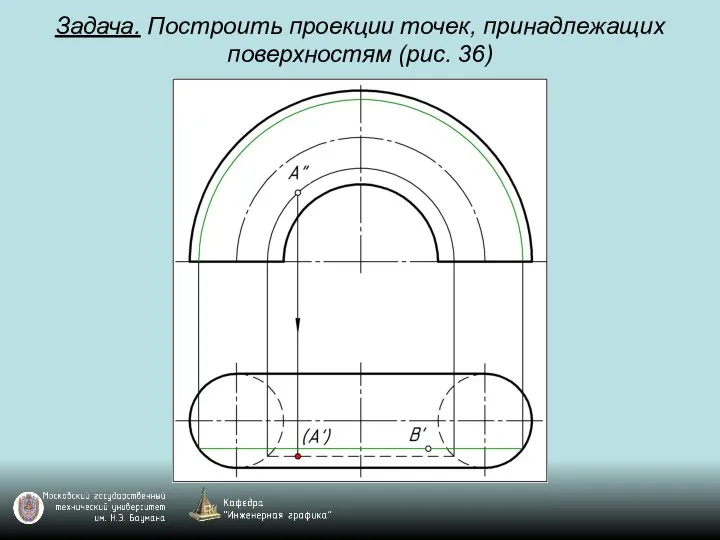
Слайд 116Задача. Построить проекции точек, принадлежащих поверхностям (рис. 36)
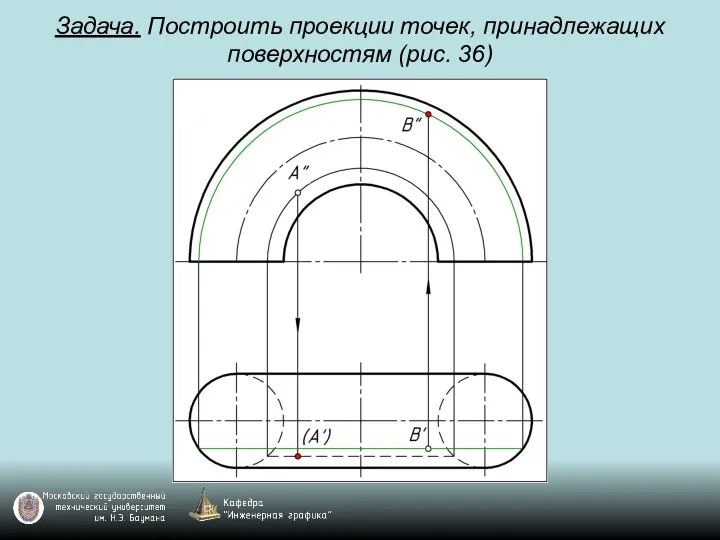
Слайд 117Винтовые поверхности
Винтовая поверхность образована винтовым движением образующей, т.е. вращением образующей вокруг

оси и одновременным перемещением вдоль оси i.
Все точки образующей gi перемещаются по винтовым линиям. Винтовая линия является направляющей d винтовой поверхности.
Ход винтовой поверхности Ph.– величина линейного перемещения точки винтовой поверхности при повороте этой точки на угол 360° вокруг оси поверхности. Ход винтовой поверхности определяется ходом винтовой линии
Винтовые поверхности различают в зависимости от параметров винтовой линии и формы образующей.
Слайд 118Чаще всего в технике применяют в качестве направляющей цилиндрическую винтовую линию, называемую

гелисой. Винтовая поверхность с прямолинейной образующей (линейчатая винтовая поверхность) с направляющей гелисой называется геликоидом.
Геликоиды разделяются на закрытые (g∩i), открытые (g ∙ i), прямые (g ┴ i), наклонные (g не ┴ i).
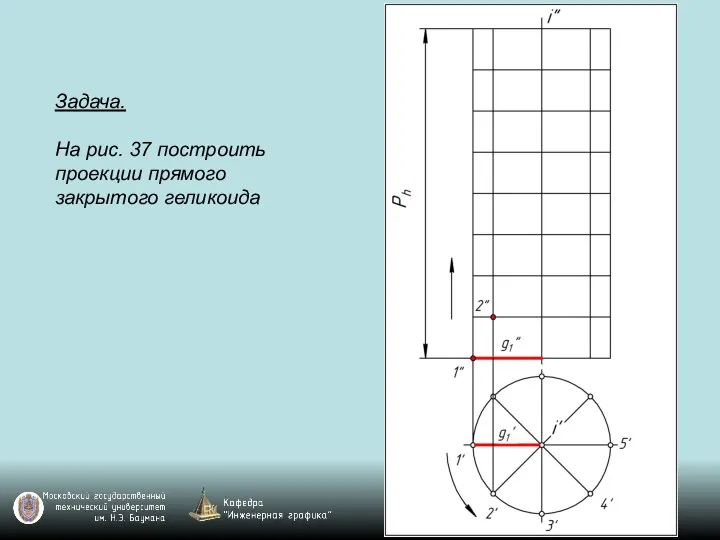
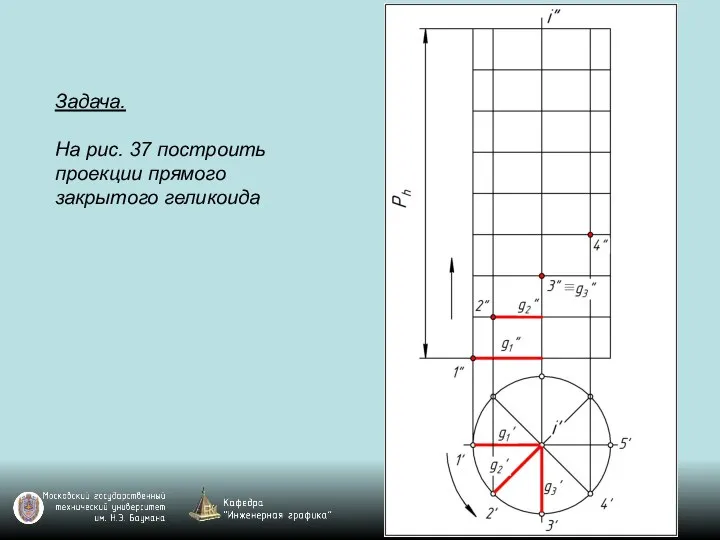
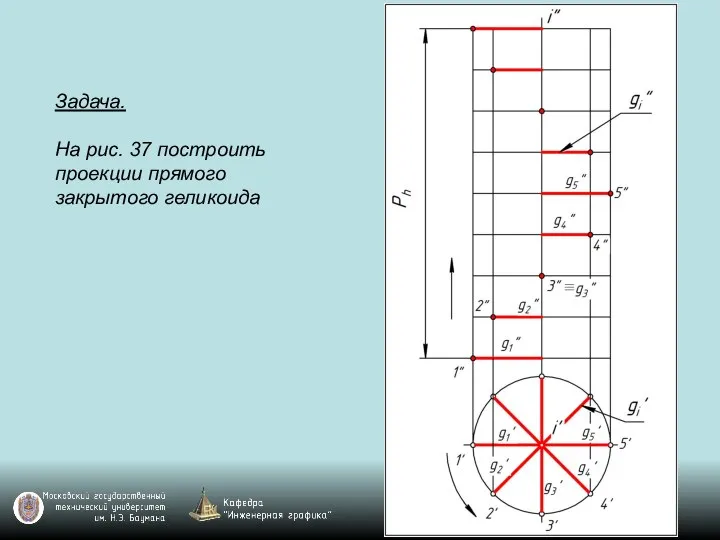
Слайд 119Задача.
На рис. 37 построить проекции прямого закрытого геликоида
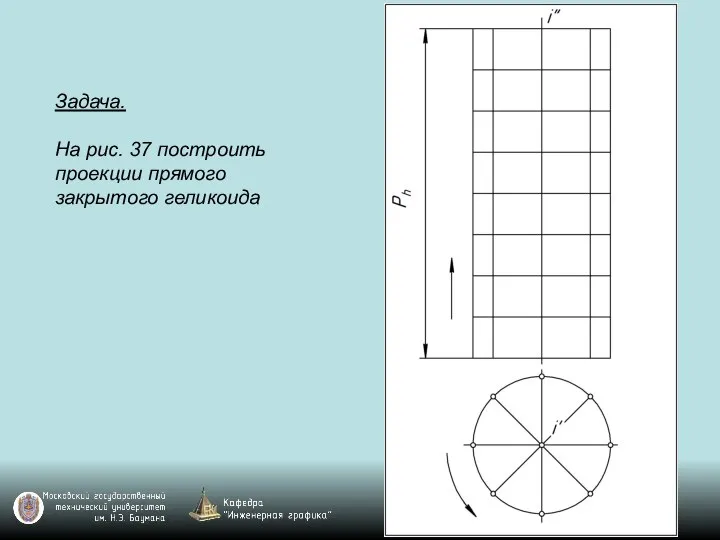
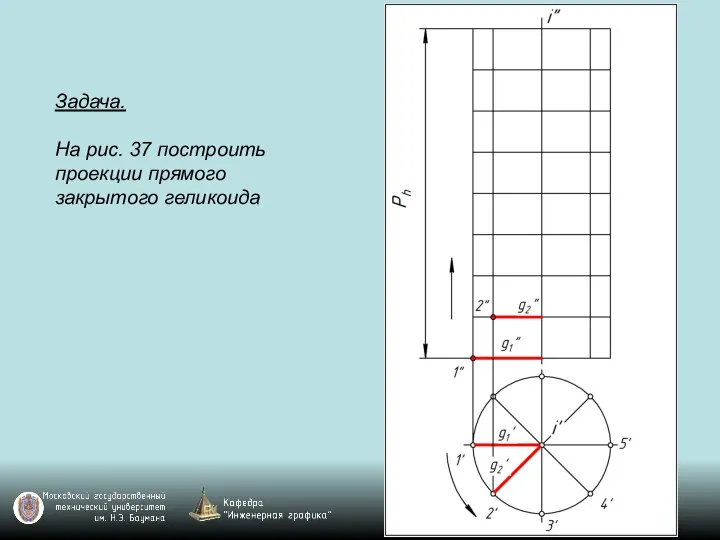
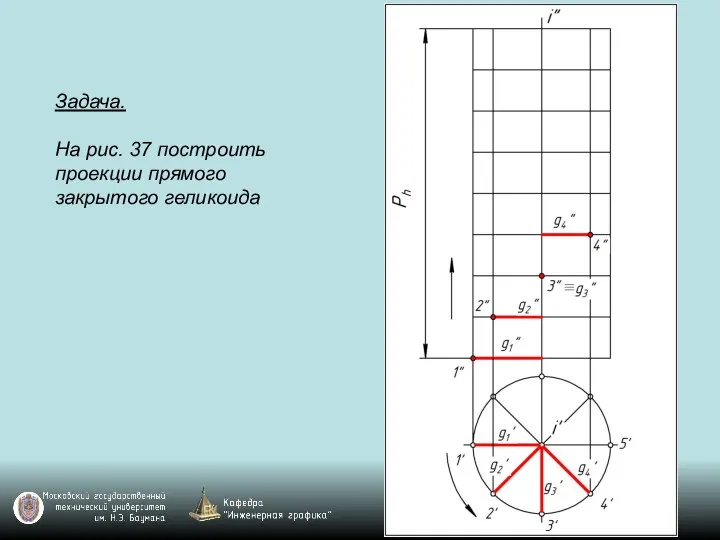
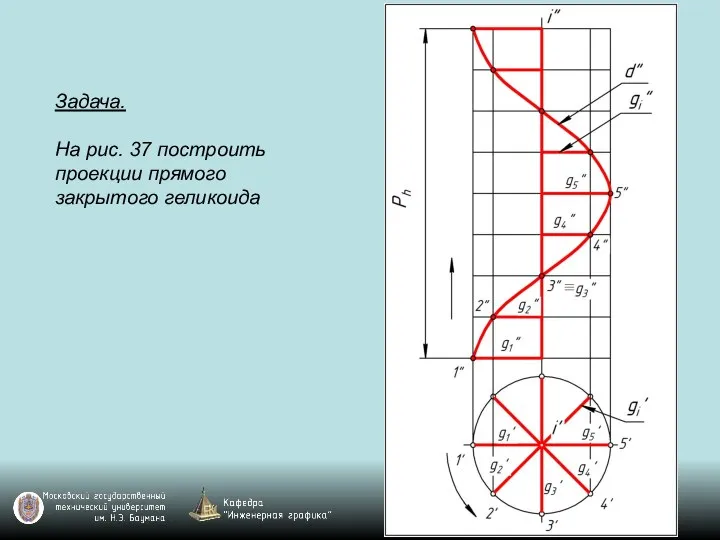
Слайд 120Задача.
На рис. 37 построить проекции прямого закрытого геликоида
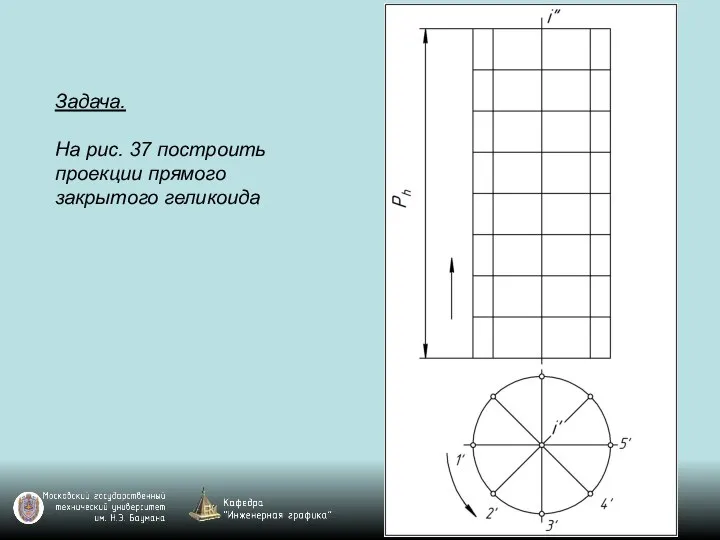
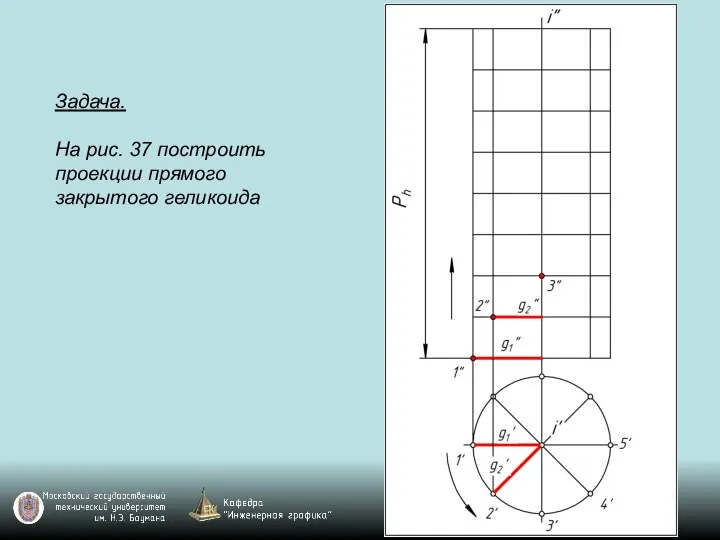
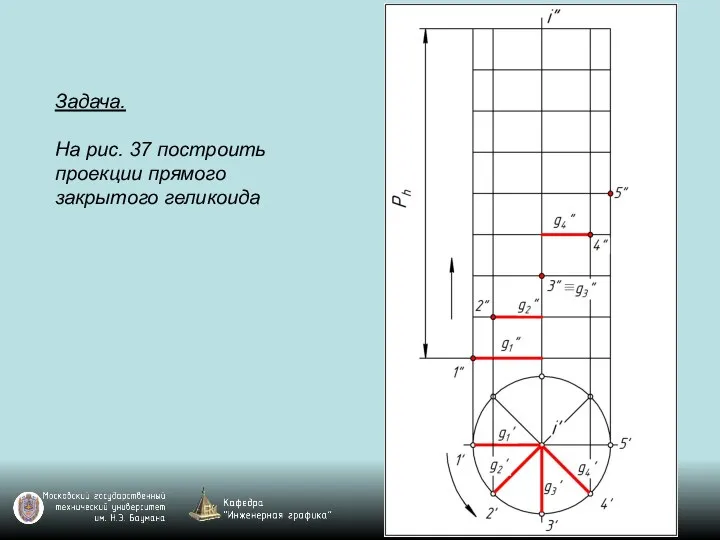
Слайд 121Задача.
На рис. 37 построить проекции прямого закрытого геликоида
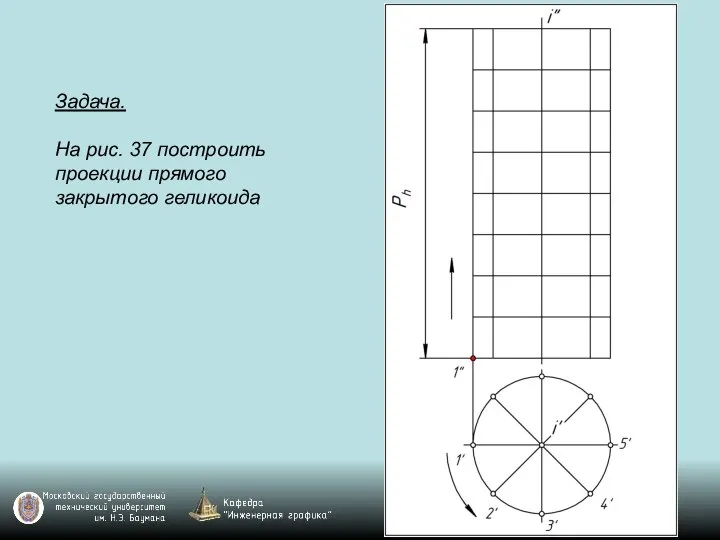
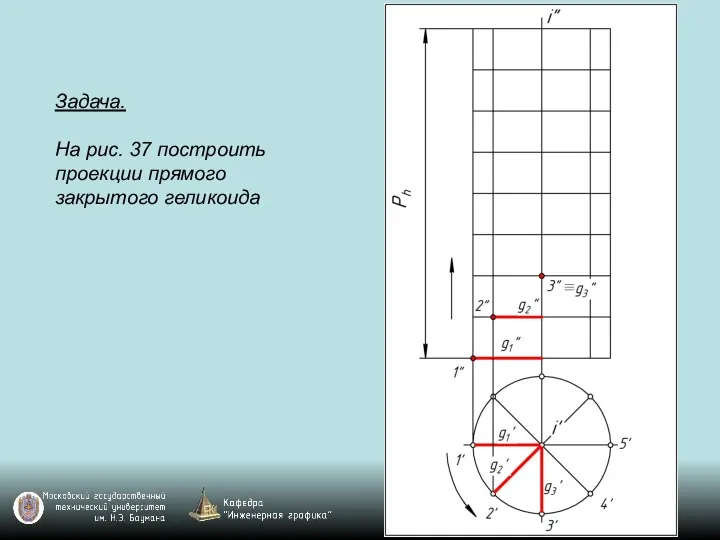
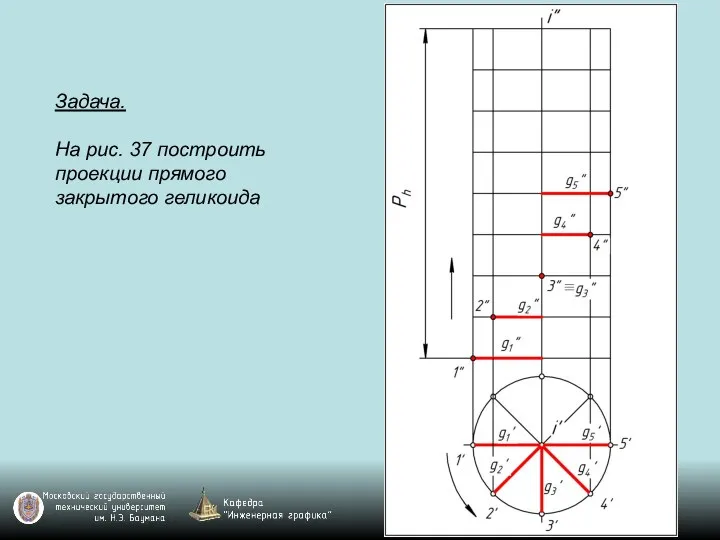
Слайд 122Задача.
На рис. 37 построить проекции прямого закрытого геликоида
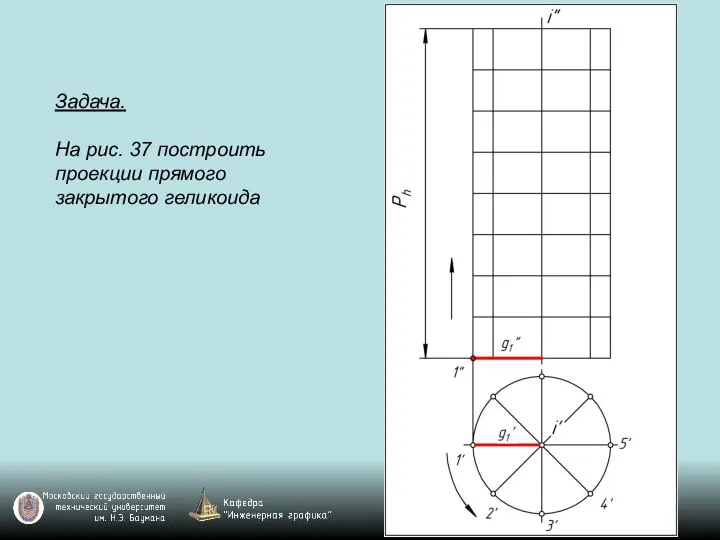
Слайд 123Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 124Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 125Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 126Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 127Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 128Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 129Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 130Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 131Задача.
На рис. 37 построить проекции прямого закрытого геликоида
Слайд 132Задача.
На рис. 37 построить проекции прямого закрытого геликоида
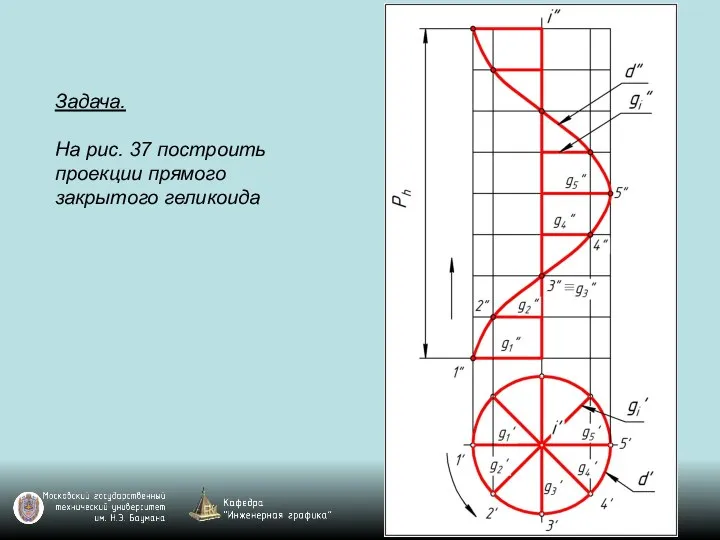
Слайд 133Задача.
На рис. 37 построить проекции прямого закрытого геликоида
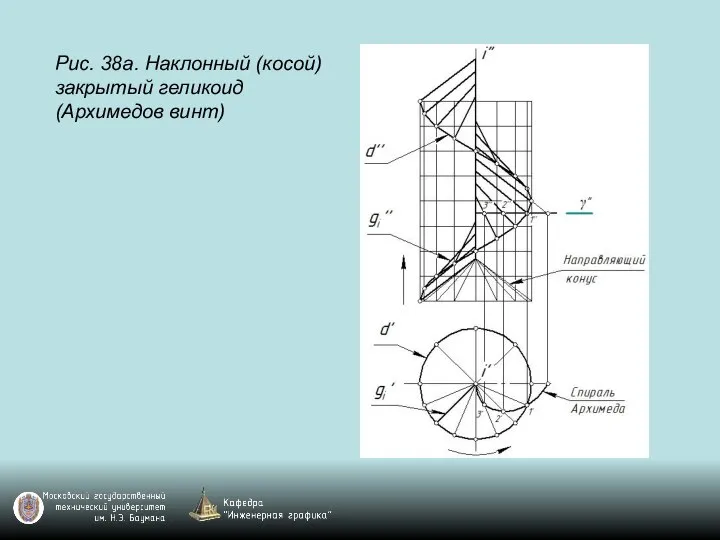
Слайд 134Рис. 38а. Наклонный (косой) закрытый геликоид (Архимедов винт)



































































































































 «М. А. Шолохов. Жизнь, творчество, личность».
«М. А. Шолохов. Жизнь, творчество, личность». Быт 4.5-8
Быт 4.5-8 Жилищная экономика и жилищная политика
Жилищная экономика и жилищная политика Материалы по гигиене и санитарии
Материалы по гигиене и санитарии Лекция по ментализму
Лекция по ментализму Gurçuklar
Gurçuklar Dreamcast — пятая и последняя игровая приставка компании Sega
Dreamcast — пятая и последняя игровая приставка компании Sega ПРЕЗЕНТАЦИЯ предприятий-дипломантов Программы «РОССИЙСКОЕ КАЧЕСТВО», лауреатов конкурса «РОССИЙСКИЙ ЛИДЕР КАЧЕСТВА» организа
ПРЕЗЕНТАЦИЯ предприятий-дипломантов Программы «РОССИЙСКОЕ КАЧЕСТВО», лауреатов конкурса «РОССИЙСКИЙ ЛИДЕР КАЧЕСТВА» организа Мастера реалистического пейзажа
Мастера реалистического пейзажа Составление текста из предложений
Составление текста из предложений крестовые походы
крестовые походы Уксусная кислота
Уксусная кислота Ethics of Translation
Ethics of Translation Коктейль из нанотехнологий в интернет-маркетинге Агапов Антон Исполнительный директор
Коктейль из нанотехнологий в интернет-маркетинге Агапов Антон Исполнительный директор Выбор ансамбля сигналов. Некогерентный случай
Выбор ансамбля сигналов. Некогерентный случай Современный учебный процесс, протекающий в условиях информатизации и массовой коммуникации всех сфер общественной жизни, требует
Современный учебный процесс, протекающий в условиях информатизации и массовой коммуникации всех сфер общественной жизни, требует Teacher’s Day
Teacher’s Day Виды организационных структур
Виды организационных структур Система сертификации в РФ
Система сертификации в РФ Искусственные нейронные сети
Искусственные нейронные сети Задачи принцессы Турандот
Задачи принцессы Турандот Способы искусственного повышения статуса говорящего
Способы искусственного повышения статуса говорящего Транспортный комплекс России
Транспортный комплекс России Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Обращение руководителя Учебного центра
Обращение руководителя Учебного центра Псалом 23. Святорусская редакция вечнозаветной псалтири
Псалом 23. Святорусская редакция вечнозаветной псалтири Дни науки и техники
Дни науки и техники НЕ с именами существительными
НЕ с именами существительными