Содержание
- 2. Изначально синдромное декодирование предназначено для обнаружения ошибок, т.е. для установления факта наличия ошибок в принимаемых кодовых
- 3. Этот процесс достаточно просто и весьма информативно отображается схемой преобразований. Для корректного декодирования необходимо, чтобы порождающая
- 4. Таким образом, можно сделать вывод что синдром – это прямая реакция на вектор ошибок. При этом
- 5. Проверочная транспонированная матрица. При использовании порождающей матрицы с явно выраженными подматрицами E и P проверочная матрица
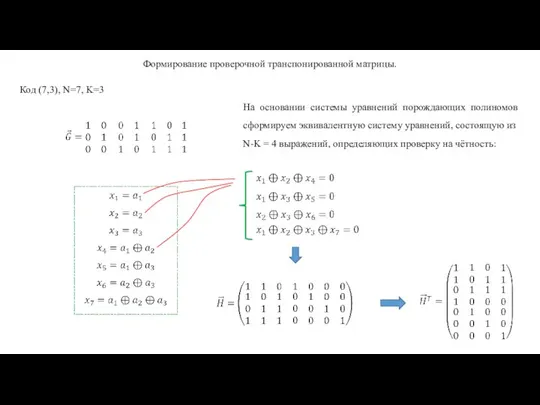
- 6. Формирование проверочной транспонированной матрицы. Код (7,3), N=7, K=3 На основании системы уравнений порождающих полиномов сформируем эквивалентную
- 7. Пример: Синдромный декодер, как видно из базовой функции и структуры проверочной матрицы, можно реализовать и программно,
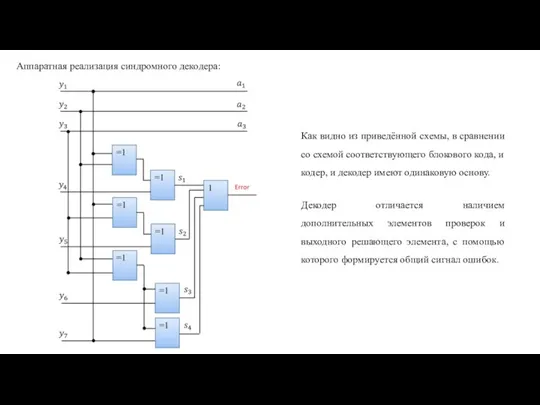
- 8. Аппаратная реализация синдромного декодера: Как видно из приведённой схемы, в сравнении со схемой соответствующего блокового кода,
- 9. Мажоритарное декодирование систематических линейных блоковых кодов Всей совокупности перечисленных условий соответствует только ограниченное количество классов кодов.
- 10. процедуры формирования частных кодовых символов xn, n=1..7, на основе информационных символов ak, k=1..3, образуют систему выражений:
- 11. Как видно из приведенных систем оценок, при оптимальном построении кода (точнее, его порождающей матрицы) количество частных
- 13. Скачать презентацию








 Государства Ближнего Востока в древности
Государства Ближнего Востока в древности САМОЕ-САМОЕ НА ЗЕМЛЕ!
САМОЕ-САМОЕ НА ЗЕМЛЕ! Forecasting Solutions Project Process
Forecasting Solutions Project Process  Угол здания.
Угол здания. Процесс начисления заработной платы
Процесс начисления заработной платы Экспериментальная работа – основа инновационной и методической работы в школе
Экспериментальная работа – основа инновационной и методической работы в школе Сложение и вычитание двузначных и однозначны чисел
Сложение и вычитание двузначных и однозначны чисел Изображение характера животных на рисунке
Изображение характера животных на рисунке Православное учение о человеке
Православное учение о человеке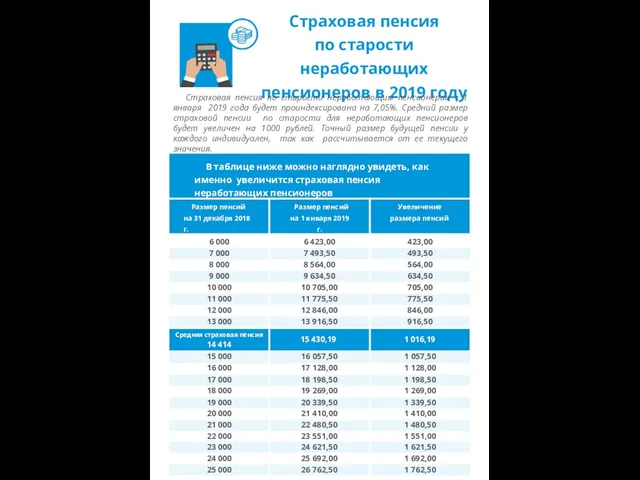 Страховая пенсия по старости неработающих пенсионеров в 2019 году
Страховая пенсия по старости неработающих пенсионеров в 2019 году Голос ребенка в интересах детского сообщества
Голос ребенка в интересах детского сообщества Кинематограф и мультипликация
Кинематограф и мультипликация ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Вена, 2007 г. Конкурентные аспекты государственного регулирования банковского бизнеса в России.
ФЕДЕРАЛЬНАЯ АНТИМОНОПОЛЬНАЯ СЛУЖБА Вена, 2007 г. Конкурентные аспекты государственного регулирования банковского бизнеса в России. Искусство: что и зачем?
Искусство: что и зачем? Включи свою ідею. Конкурсна робота
Включи свою ідею. Конкурсна робота Концепция создания интеграционной информационной системы «Единое окно по экспортно-импортным операциям»
Концепция создания интеграционной информационной системы «Единое окно по экспортно-импортным операциям»  Самопознание: в стремлении к самосовершенствованию
Самопознание: в стремлении к самосовершенствованию Значение обязательности подготовки граждан к военной службе
Значение обязательности подготовки граждан к военной службе Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Меры гарантийной и финансовой поддержки субъектов МСП Ивановским государственным фондом поддержки малого предпринимательства
Меры гарантийной и финансовой поддержки субъектов МСП Ивановским государственным фондом поддержки малого предпринимательства Белсенді саяхат түрлерінде тәсілдік өңдеуді құрудың тәсілі мен
Белсенді саяхат түрлерінде тәсілдік өңдеуді құрудың тәсілі мен Табличный процессор Excel 2007
Табличный процессор Excel 2007 Космический маятник
Космический маятник Заполните таблицу
Заполните таблицу Quality Control System in Germany Система Контроля Качества в Германии Dr. Ulrike Bickelmann Federal Office for Agriculture and Food – Germany Федеральное агентство по сельском
Quality Control System in Germany Система Контроля Качества в Германии Dr. Ulrike Bickelmann Federal Office for Agriculture and Food – Germany Федеральное агентство по сельском Сопротивление движению поезда
Сопротивление движению поезда Презентация на тему Галилеевы спутники Юпитера
Презентация на тему Галилеевы спутники Юпитера ИСТОРИЯ ПРЕДПРИЯТИЯ ТЕХНОЛОГИИ
ИСТОРИЯ ПРЕДПРИЯТИЯ ТЕХНОЛОГИИ