ЛЕКЦИЯ №1 Метод-точка-прямая

Лекция 1

Начертательная геометрия изучает методы построения изображений пространственных объектов на плоскости.

Базовые геометрические элементы начертательной геометрии

Точка – абстрактное математическое понятие. Не имеет измерений - нульмерный объект .
Линия – непрерывное одномерное множество точек ( цепочка точек). Непрерывная последо-вательность положений точки, перемещаю-щейся в пространстве по определенному закону (траектории). Измерение : только длина. Толщины нет.
Поверхность – непрерывное двумерное мно-жество точек. Непрерывная последователь-ность положений линии, перемещающейся в пространстве по определенному закону. Измерения : длина, ширина, площадь. Толщины и объема нет.

Проективное
пространство

Для устранения неоднородности Евклидова пространства
условно принято -
(a  b  c…)  (a ∩ b ∩ c… = F )
параллельные между собой прямые
пересекаются
в бесконечно удаленной точке F -
несобственной точке пространства.
Евклидово пространство, дополненное несобственными элементами, называют проективным.

Изображение геометрических объектов

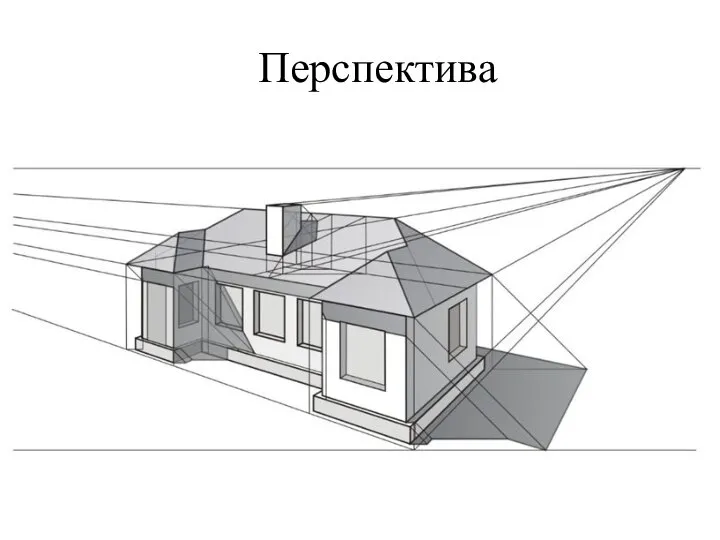
Перспектива

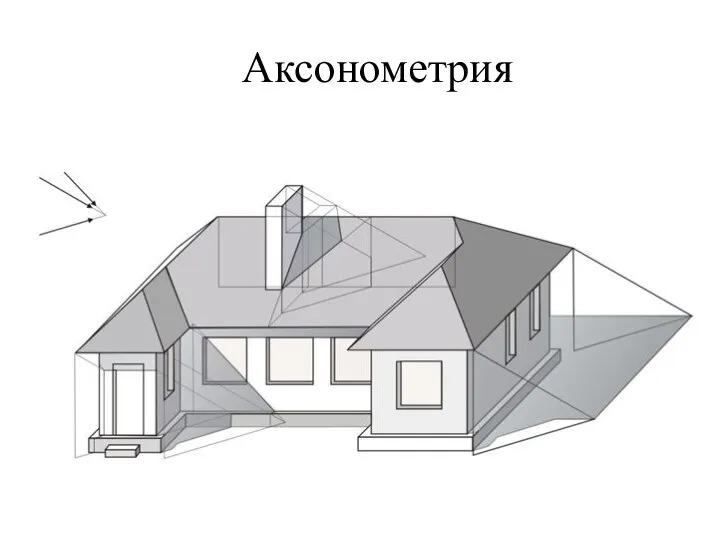
Аксонометрия

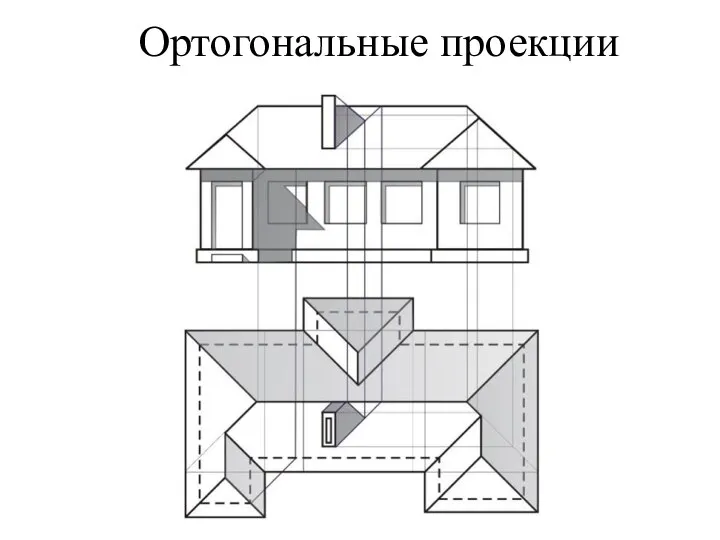
Ортогональные проекции

Метод проецирования

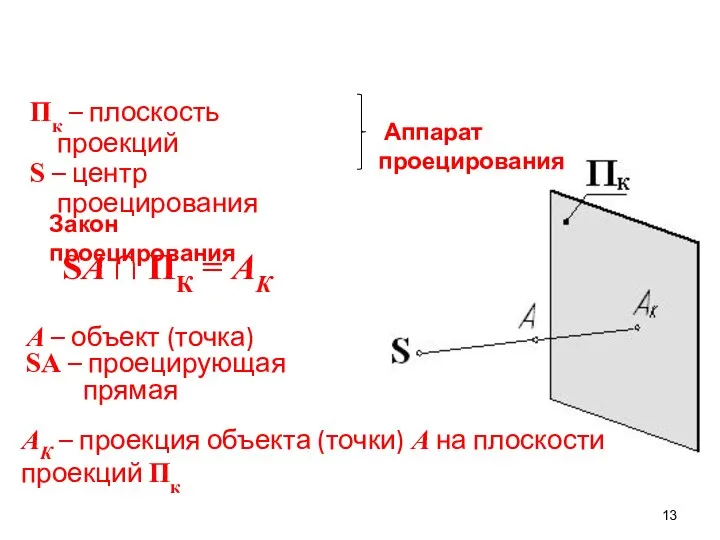
А – объект (точка)
SA – проецирующая
прямая
SA ∩ ПК = АК
АК – проекция объекта (точки) А на плоскости проекций Пк
Пк – плоскость проекций
S – центр проецирования
Аппарат проецирования
Закон проецирования

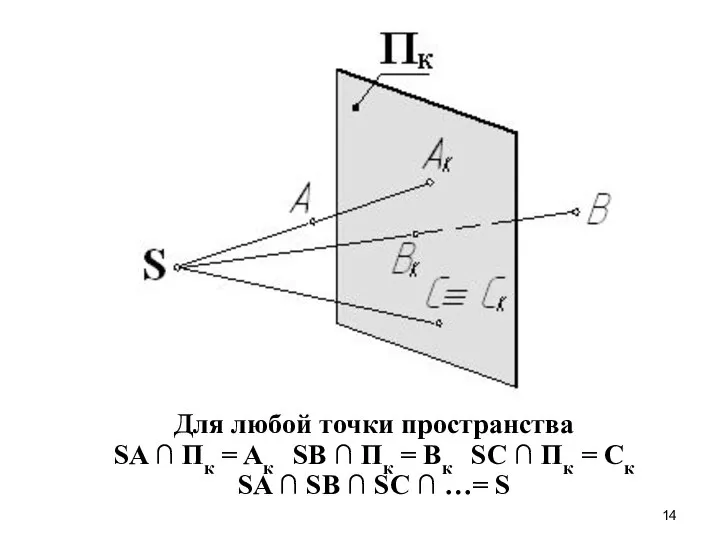
Для любой точки пространства
SA ∩ Пк = Aк SВ ∩ Пк = Bк SС ∩ Пк = Cк
SA ∩ SВ ∩ SС ∩ …= S

Варианты метода проецирования

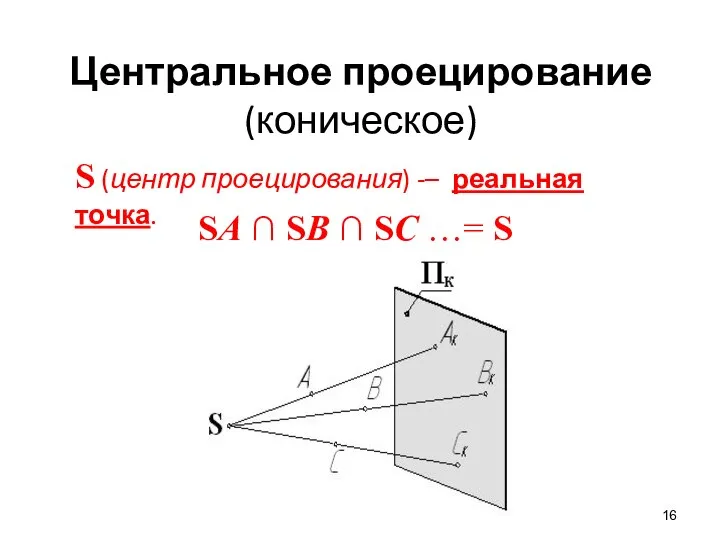
Центральное проецирование
(коническое)
S (центр проецирования) -– реальная точка.
SA ∩ SB ∩ SC …= S

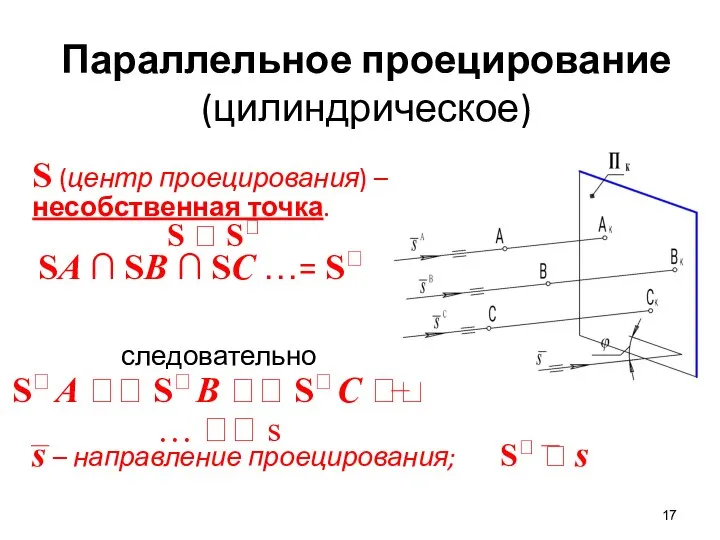
Параллельное проецирование
(цилиндрическое)
S (центр проецирования) –
несобственная точка.
S  S
SA ∩ SB ∩ SC …= S
следовательно
S A  S B  S C  …  s
s – направление проецирования; S  s

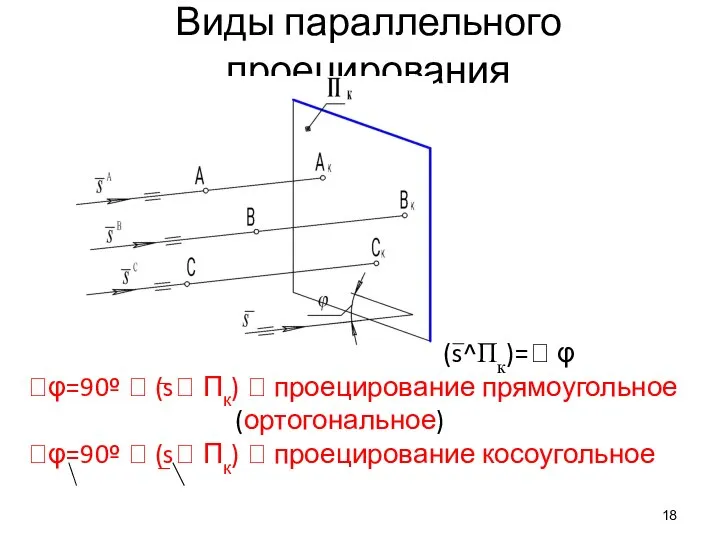
Виды параллельного проецирования
(s^Пк)= φ
φ=90º  (s Пк)  проецирование прямоугольное (ортогональное)
φ=90º  (s Пк)  проецирование косоугольное

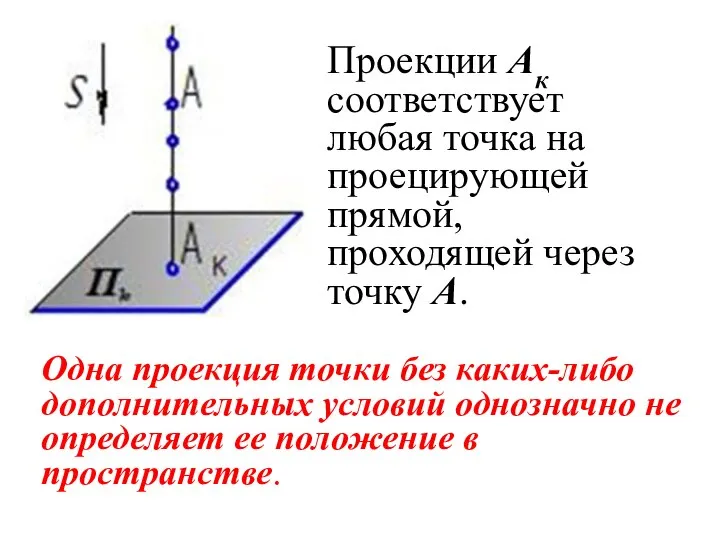
Проекции Ак соответствует любая точка на проецирующей прямой, проходящей через точку А.
Одна проекция точки без каких-либо дополнительных условий однозначно не определяет ее положение в пространстве.

Метод Монжа

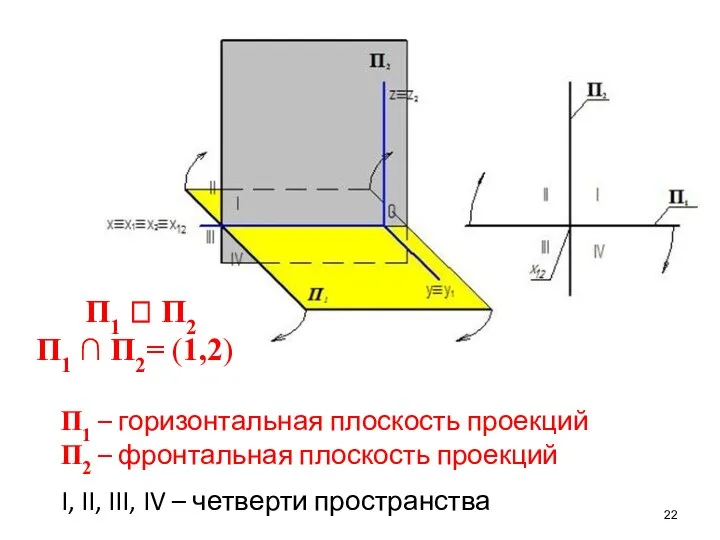
П1  П2
П1 ∩ П2= (1,2)
П1 – горизонтальная плоскость проекций
П2 – фронтальная плоскость проекций
I, II, III, IV – четверти пространства

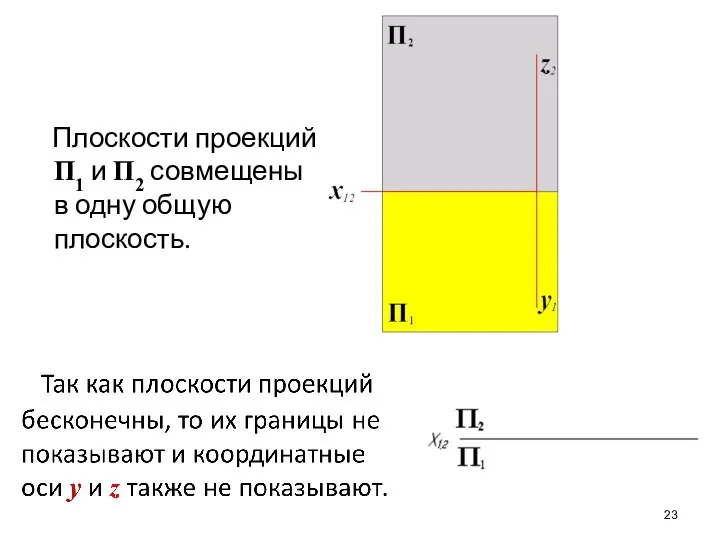
Плоскости проекций П1 и П2 совмещены в одну общую плоскость.

Проецирование точки

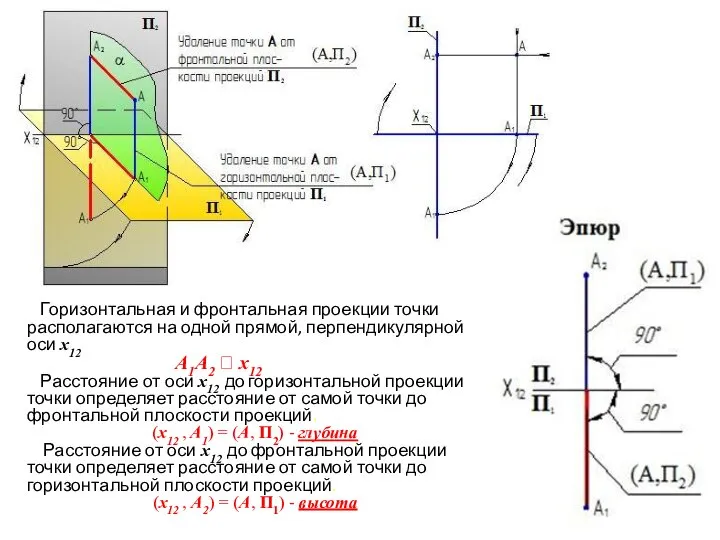
Горизонтальная и фронтальная проекции точки располагаются на одной прямой, перпендикулярной оси x12
А1А2  х12
Расстояние от оси x12 до горизонтальной проекции точки определяет расстояние от самой точки до фронтальной плоскости проекций.
(х12 , А1) = (А, П2) - глубина
Расстояние от оси x12 до фронтальной проекции точки определяет расстояние от самой точки до горизонтальной плоскости проекций.
(х12 , А2) = (А, П1) - высота

Ортогональные проекции точки на две взаимно перпендикулярные плоскости однозначно определяют положение точки в пространстве и делают изображения обратимыми.

Проецирование
прямой линии

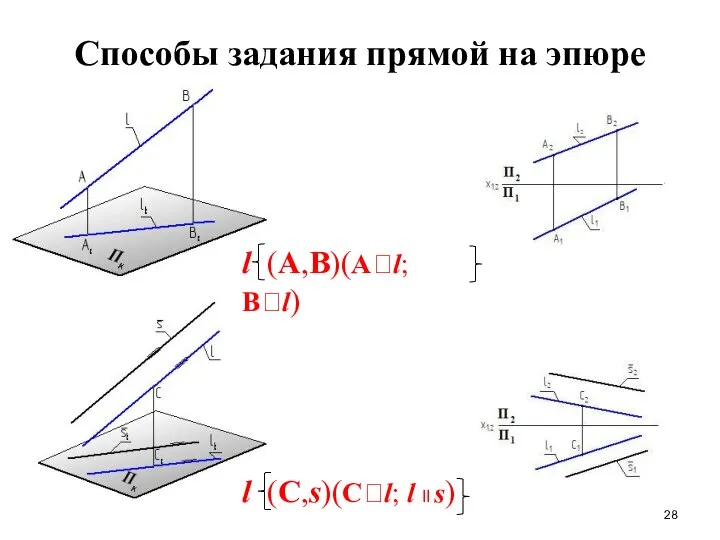
Способы задания прямой на эпюре
l (A,B)(Al; Bl)
l (С,s)(Cl; l ll s)

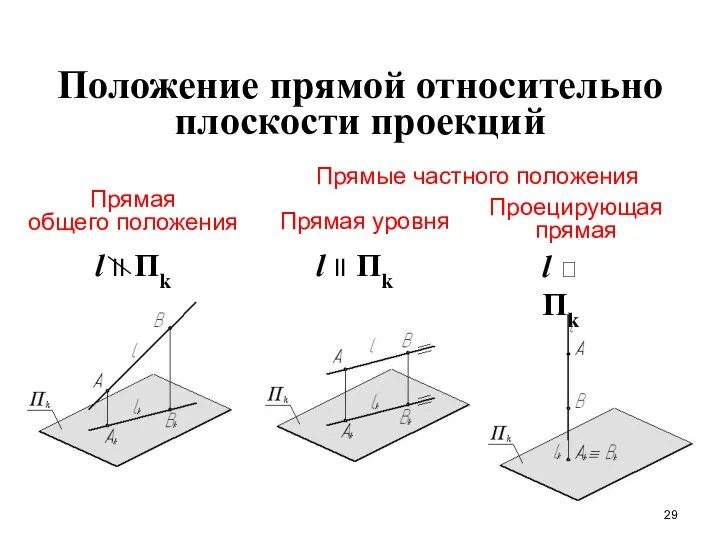
Положение прямой относительно
плоскости проекций
Прямая
общего положения
Прямые частного положения
l II Пk
l II Пk
l  Пk
Прямая уровня
Проецирующая
прямая

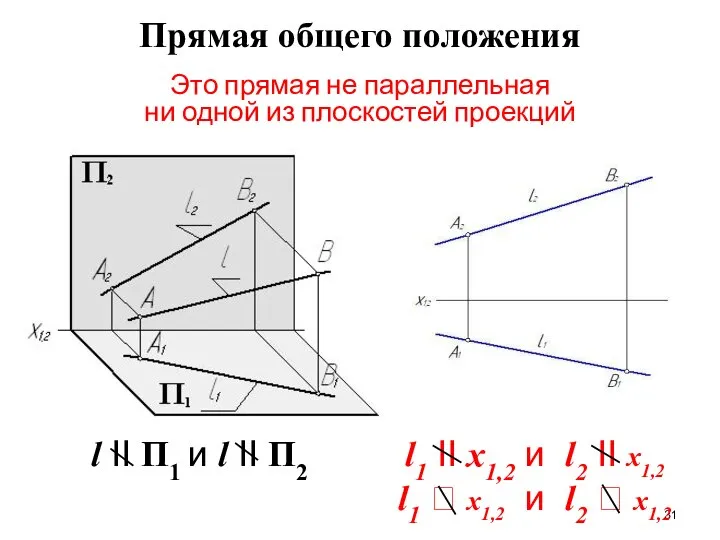
l II П1 и l II П2
l1 II x1,2 и l2 II x1,2
l1  x1,2 и l2  x1,2
Прямая общего положения
Это прямая не параллельная
ни одной из плоскостей проекций

Прямые уровня
Это прямые параллельные
какой-либо одной
плоскости проекций
l II Пк

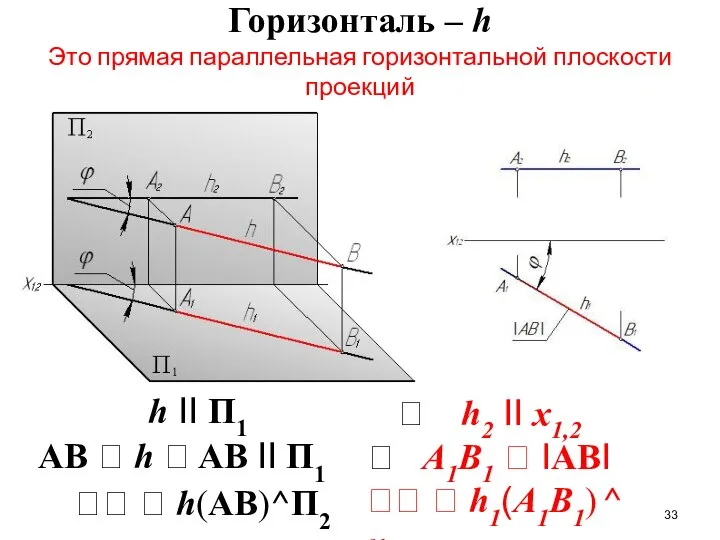
Горизонталь – h
Это прямая параллельная горизонтальной плоскости проекций
h II П1
AB  h  AB II П1
  h(AB)^П2
 h2 II x1,2
 А1В1  IABI
  h1(А1В1) ^ x1,2

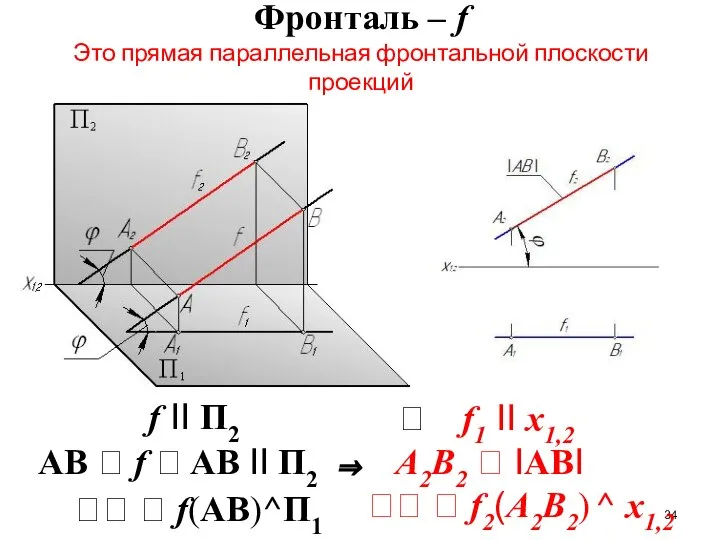
Фронталь – f
Это прямая параллельная фронтальной плоскости проекций
f II П2
AB  f  AB II П2
  f(AB)^П1
 f1 II x1,2
А2В2  IABI
  f2(А2В2) ^ x1,2

Характерная особенность эпюра горизонтали и фронтали –
одна из проекций параллельна координатной оси х1,2

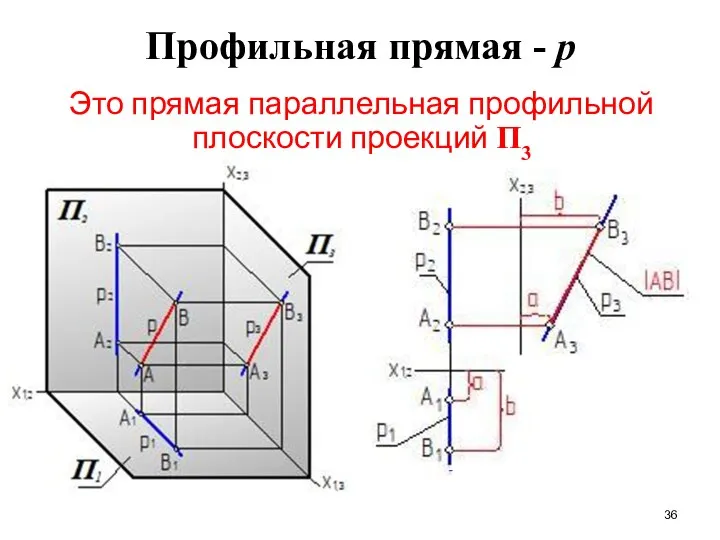
Профильная прямая - p
Это прямая параллельная профильной плоскости проекций П3

Проецирующие прямые
Это прямые перпендикулярные
какой-либо одной
плоскости проекций
l  Пк

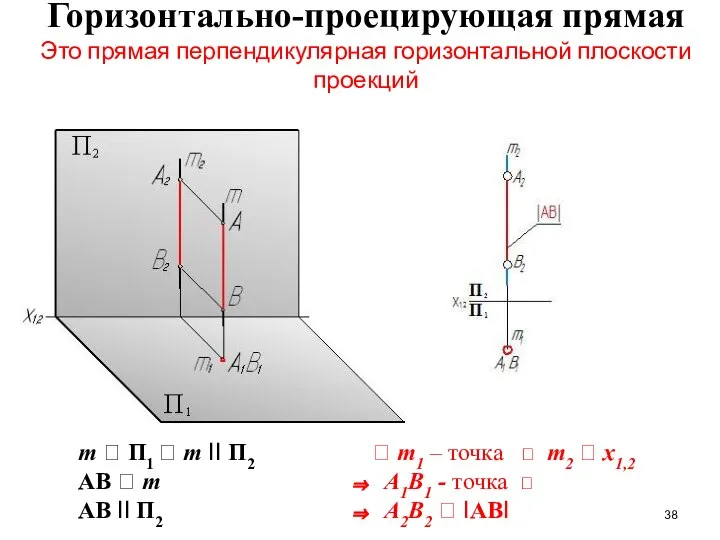
Горизонтально-проецирующая прямая
Это прямая перпендикулярная горизонтальной плоскости проекций
m  П1  m II П2
AB  m
AB II П2
 m1 – точка  m2  x1,2
А1В1 - точка 
А2В2  IABI

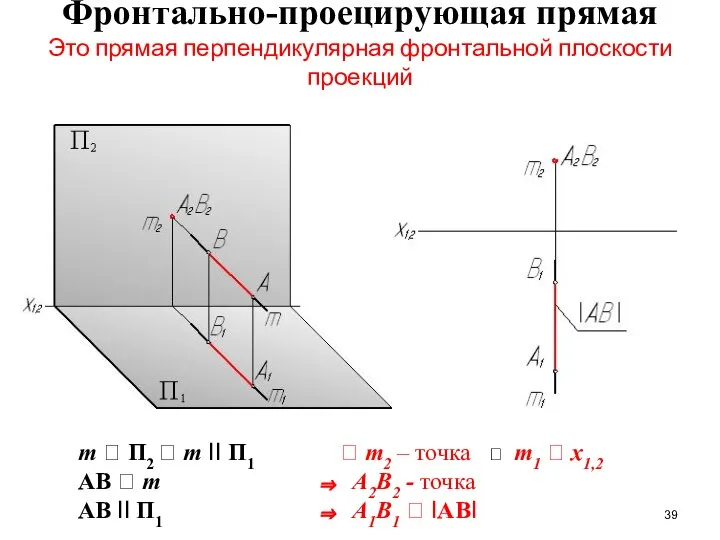
Фронтально-проецирующая прямая
Это прямая перпендикулярная фронтальной плоскости проекций
m  П2  m II П1
AB  m
AB II П1
 m2 – точка  m1  x1,2
А2В2 - точка
А1В1  IABI

Характерная особенность эпюра проецирующей прямой –
одна из проекций прямой точка

Взаимное положение двух прямых

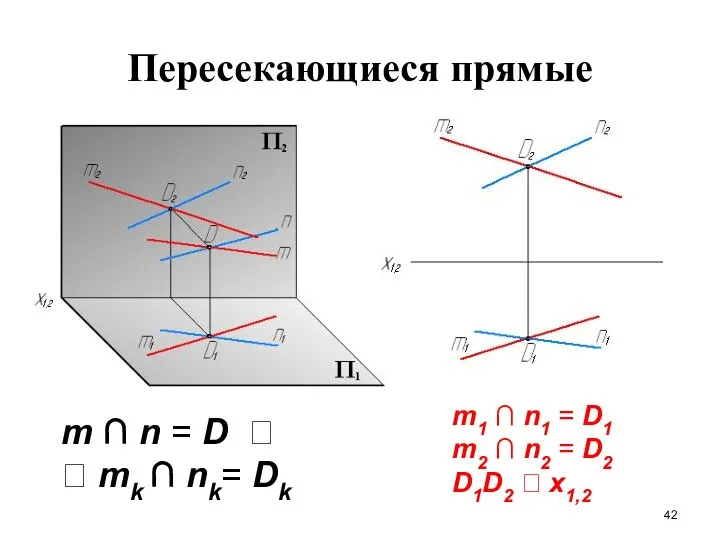
Пересекающиеся прямые
m ∩ n = D 
 mk ∩ nk= Dk
m1 ∩ n1 = D1
m2 ∩ n2 = D2
D1D2  x1,2

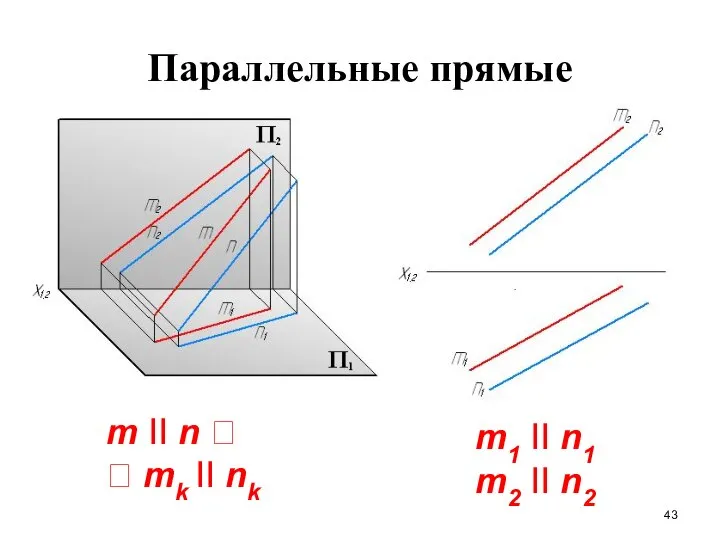
Параллельные прямые
m II n 
 mk II nk
m1 II n1
m2 II n2